Druyd:Knowledge

Évaporation

Storyboard

ID:(661, 0)

Chaleur latente

Définition

Le principe de mesure de la chaleur latente consiste à effectuer un changement de phase et à mesurer l'énergie requise, comme illustré dans l'image suivante :

De cette manière, il est possible d'estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à la chaleur latente mesurée en J/kg ou en J/mol.

ID:(13543, 0)

Mécanismes

Image

ID:(15288, 0)

Mesure de la chaleur d'évaporation

Noter

La mesure de la chaleur de vaporisation s'effectue en chauffant un échantillon, provoquant ainsi son évaporation, tout en mesurant simultanément la chaleur fournie à l'échantillon. Ensuite, la vapeur est refroidie et condensée, et la masse originellement évaporée est mesurée.

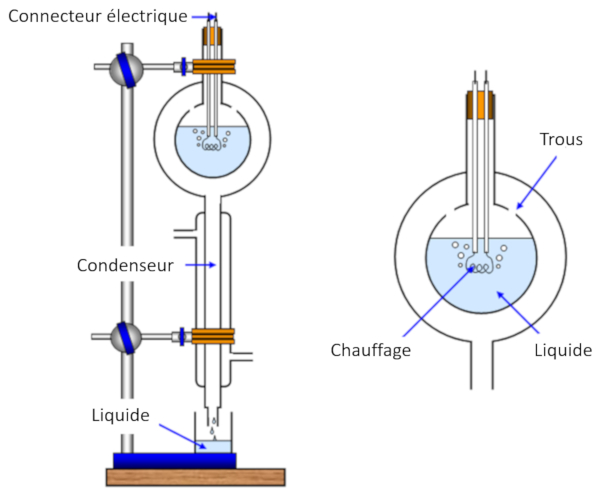
De cette manière, nous pouvons estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à ERROR:5238,0 mesuré en joules par kilogramme (J/kg) ou joules par mole (J/mol).

ID:(1662, 0)

Mesure de la chaleur de fusion

Citation

La mesure de la chaleur de vaporisation s'effectue en chauffant un échantillon, provoquant son évaporation tout en mesurant la chaleur fournie à l'échantillon. Ensuite, la vapeur est refroidie et condensée, et la masse qui a initialement évaporé est mesurée.

Ce processus permet d'estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à la chaleur latente mesurée en J/kg ou J/mol.

ID:(13541, 0)

Modèle

Exercer

ID:(15346, 0)

Quantité de vapeur d'eau

Équation

Lorsque a variation de volume en changement de phase ($\Delta V$) change de phase, passant d'un liquide à un gaz, cela peut être exprimé comme suit :

$\Delta V = V_{\text{gaz}} - V_{\text{liquide}}$

Étant donné que le volume du gaz est nettement supérieur à celui du liquide,

$V_{\text{gaz}} \gg V_{\text{liquide}}$

nous pouvons approximativement écrire :

$\Delta V \approx V_{\text{gaz}}$

Comme la vapeur d'eau se comporte de manière similaire à un gaz idéal, nous pouvons affirmer qu'avec les valeurs de a constante du gaz universel ($R_C$), le nombre de taupes ($n$), a température absolue ($T$) et a pression de vapeur d'eau non saturée ($p_v$) :

$ p V = n R_C T $

ainsi, a variation de volume en changement de phase ($\Delta V$) est :

$\Delta V = \displaystyle\frac{nRT}{p_v}$

ID:(3185, 0)