Weiss model
Storyboard 
Weiss's model assumes that a mean field can be defined in which each spin is located and that is formed from the average of the spin that surrounds it. In this way it is relatively simple to calculate the partition function and determine how the solid is magnetized.
ID:(539, 0)
Solución gráfica del método de Weiss
Definition 
La ecuación de Weiss
| $2 J n s B_s(\eta)= k_B T \eta - g \mu_B H_0 $ |
puede ser resuelta igualando la función de Brillouin del lado izquierdo con la recta del lado derecho. Esto es gráficamente
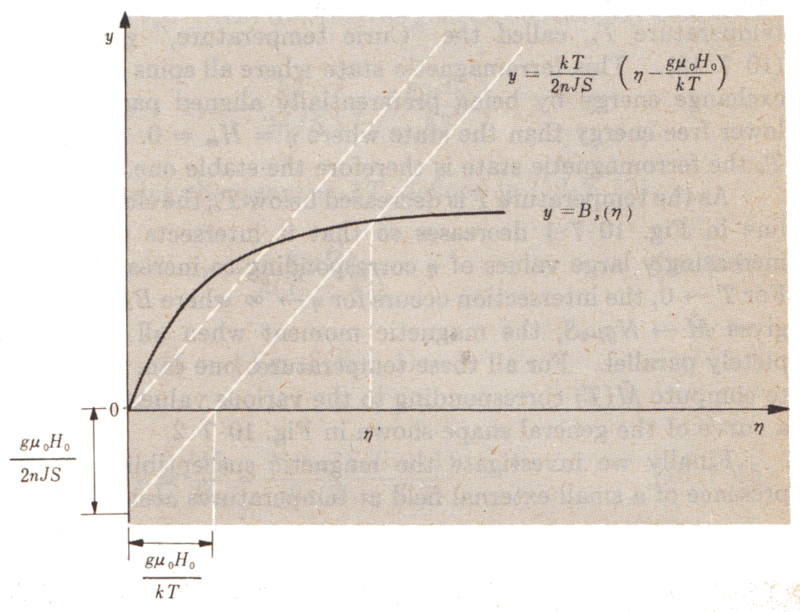
Hay que hacer notar que si la temperatura es demasiado alta existe una solución para el caso en que no hay campo magnético (des-magnetización).
ID:(13510, 0)
Weiss model
Storyboard 
Weiss's model assumes that a mean field can be defined in which each spin is located and that is formed from the average of the spin that surrounds it. In this way it is relatively simple to calculate the partition function and determine how the solid is magnetized.
Variables
Calculations
Calculations
Equations
Examples
El hamiltoneando se puede escribir como la suma de hamiltoneanos en torno de un tomo
con lo que la parte de interacci n queda como una correcci n que se comporta como una campo magn tico generado por los vecinos.
Por ello se puede definir un campo medio con
El factor
Con
${\cal H}_j=-\left(g\gamma H_0+2J\displaystyle\sum_{k=1}^nS_{kz}\right)S_{jz}$
se puede estimar con
En el caso de un hamiltoenano con
Como el spin es con
$\mu_B=\gamma\hbar$
y con
Con los niveles de energ a con
$H=H_0+\bar{H}$
\\n\\nes\\n\\n
$Z_W=\displaystyle\sum_{m=-s}^{s}e^{-\eta m}$
\\n\\ncon\\n\\n
$\eta = \beta g \mu_BH$
que se puede sumar y arroja con
Las ecuaciones dependen del factor\\n\\n
$\eta = \beta g\mu_BH$
\\n\\nque con la definici n de
$\beta=\displaystyle\frac{1}{k_BT}$
se obtiene con
El momento magn tico medio corresponde a la fuerza generalizada asociada a la variable campo magn tico. Por ello\\n\\n
$\bar{S}_{jz}=\displaystyle\frac{1}{\beta}\displaystyle\frac{\partial\ln Z_W}{\partial H}$
\\n\\nlo que en este caso da\\n\\n
$\bar{S}_{jz}=g\mu_B[(S+\frac{1}{2})\coth(S+\frac{1}{2})\eta-\frac{1}{2}\coth\frac{1}{2}\eta]$
El factor de las funciones del cotangente hiperb lico se puede escribir como la funci n de Brillouin
La definici n de la funci n de Brillouin se escribe con
El problema del calculo del momento magn tico con
es que
$\eta =\displaystyle\frac{\mu_BB}{k_BT} =\displaystyle\frac{\mu_B}{k_BT}(H_0+\bar{H})$
se tiene finalmente una ecuaci n para calcular
La ecuaci n de Weiss
puede ser resuelta igualando la funci n de Brillouin del lado izquierdo con la recta del lado derecho. Esto es gr ficamente
Hay que hacer notar que si la temperatura es demasiado alta existe una soluci n para el caso en que no hay campo magn tico (des-magnetizaci n).
Para que exista una soluci n de magnetizaci n espontanea la pendiente de la funci n de Brillouin en el origen debe ser mayor que la de la recta o sea\\n\\n
$\displaystyle\frac{dB_s}{d\eta}>\displaystyle\frac{k_BT}{2nJs}$
\\n\\nComo la para valores peque os de
$B_s(\eta)\sim \displaystyle\frac{1}{3}(s+1)\eta$
se tiene que existe magnetizaci n espontanea siempre que la temperatura sea inferior a la llamada temperatura de Curie que con
Para el caso
$B_S(\eta)=\displaystyle\frac{k_BT}{2JnS}\left(\eta-\displaystyle\frac{g\mu_BH_0}{k_BT}\right)$
\\n\\npor lo que la ecuaci n para el calculo del $\eta$ queda como\\n\\n
$2nJ\displaystyle\frac{1}{3}(S+1)S\eta=k_BT\left(\eta-\displaystyle\frac{g\mu_BH_0}{k_BT}\right)$
\\n\\nque con la expresi n para la temperatura de Curie\\n\\n
$T_c=\displaystyle\frac{2nJS(S+1)}{3k_B}$
queda con
La magnetizaci n de calcula de la suma de los spines individuales multiplicados por la permeabilidad magn tica.
Con
$\bar{M} = \mu\displaystyle\sum_{j=1}^N \bar{S}_{jz}=\mu N g\mu_B s B_s(\eta)$
o sea con
La susceptibilidad magn tica se calcula dividiendo la magnetizaci n media que es con
y la relaci n para el
$\chi=\displaystyle\frac{\partial \bar{M}}{\partial H}=\displaystyle\frac{\partial \bar{M}}{\partial \eta}\displaystyle\frac{\partial \eta}{\partial H}=g\mu\mu_B s N\displaystyle\frac{\partial B_s(\eta)}{\partial \eta}\displaystyle\frac{\partial \eta}{\partial H}$
resulta con
ID:(539, 0)
