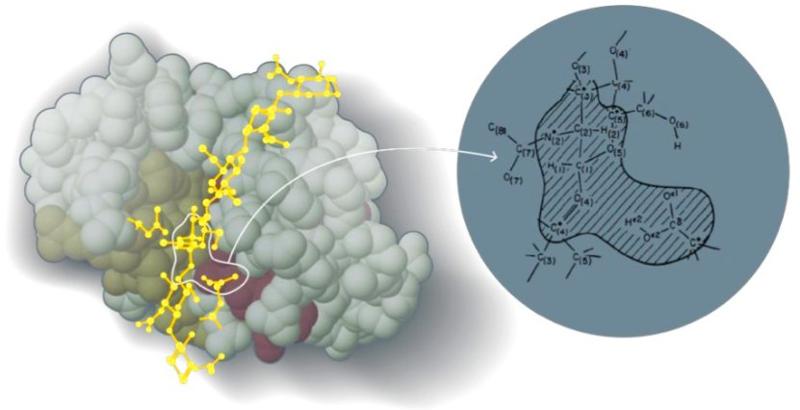
Presi n microscopica

(ID 1706)

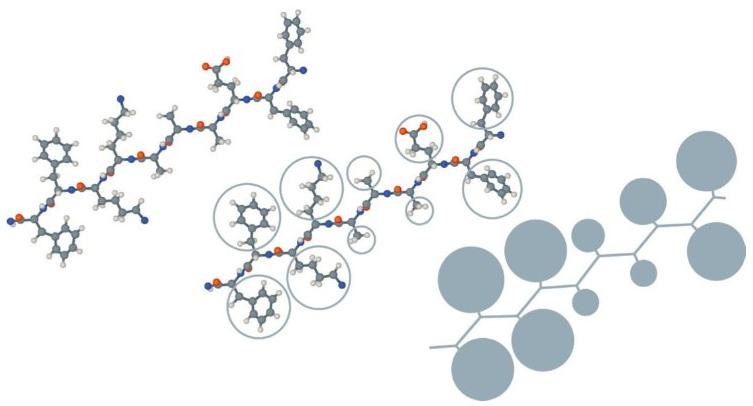
Teor a Cin tica

(ID 1707)

La ecuaci n de estado de un gas ideal depende de la presi n p, el volumen V, el numero de moles n, la temperatura absoluta T y la constante universal de los gases:

(ID 3938)

Con la expresi n para la presi n\\n\\n

$p=\displaystyle\frac{2}{3}c_n\langle\epsilon\rangle$

la definici n de la concentraci n en funci n del numero de part culas N y el volumen V

\\n\\ny la relaci n del numero de part culas con el numero de moles n y el numero de Avogadro N_A\\n\\n

$N=nN_A$

se tiene la ecuaci n de estado que

(ID 3223)

La concentraci n se define como el numero N de part culas por volumen V:

(ID 3936)

Si se compara la ecuaci n de estado derivada en forma microsc pica\\n\\n

$pV=\displaystyle\frac{2}{3}nN_A\langle\epsilon\rangle$

con la ecuaci n de estado de los gases ideales

\\n\\nse concluye que la energ a de una part cula es\\n\\n

$\langle\epsilon\rangle=\displaystyle\frac{3RT}{2N_A}$

La constante R/N_A se conoce como la constante de Boltzmann

(ID 3939)