Momento de inercia
Storyboard 
El momento de inercia es el factor en rotación que equivale a la masa en la traslación.El momento de inercia se puede determinar empíricamente haciendo rotar un cuerpo en torno a un eje o calculando como se distribuye la masa en torno al eje.
ID:(600, 0)
Barra que rota en torno a un eje $\perp$
Imagen 
Una barra de masa $m$ y longitud $l$ que gira alrededor de su centro, que coincide con el centro de masa:
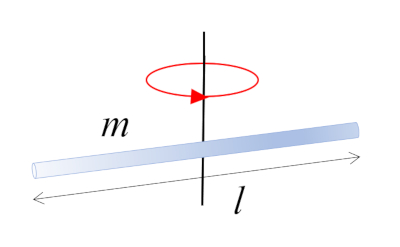
ID:(10962, 0)
Cilindro que rota en torno a eje $\parallel$
Imagen 
Una rotación de un cilindro con masa $m$ y radio $r$ alrededor del eje del cilindro, donde el centro de masa (CM) se encuentra a media altura:
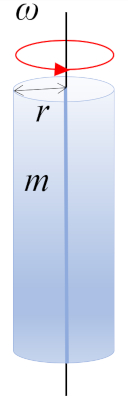
ID:(10964, 0)
Cilindro que rota en torno a eje $\perp$
Imagen 
En esta situación, un cilindro con masa $m$, radio $r$ y altura $h$ está girando alrededor de un eje que es perpendicular a su propio eje. Este eje pasa por el punto medio de la longitud del cilindro, donde se localiza el centro de masa (CM):
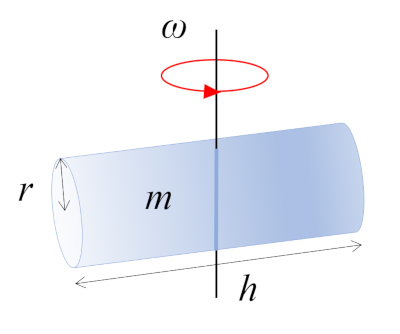
ID:(10965, 0)
Momento de inercia de paralelepípedo regular
Imagen 
Un paralelepípedo rectángulo con masa $m$, lados $a$ y $b$, y perpendicular al eje de rotación, está girando alrededor de su centro de masa, que se encuentra en el centro geométrico del cuerpo:
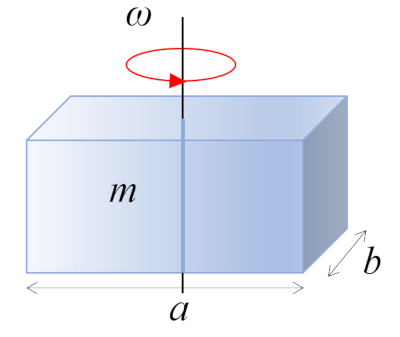
ID:(10973, 0)
Paralelepípedo recto
Imagen 
Para un paralelepípedo recto con masa $m$ y lado $a$, el centro de masa se encuentra en el centro geométrico:
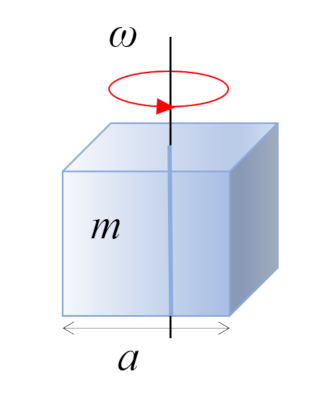
ID:(10963, 0)
Esfera
Imagen 
Una esfera con masa $m$ y radio $r$ está girando alrededor de su centro de masa, el cual se encuentra en el centro de la esfera:
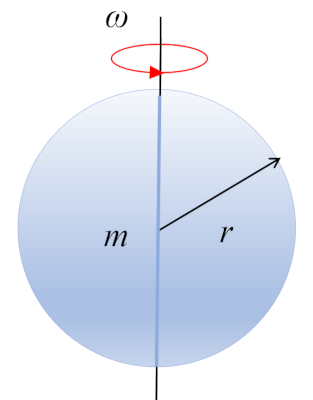
ID:(10490, 0)
