Utilisateur:
Trajectoire balistique
Storyboard 
Si un objet est lancé ou tiré dans un champ gravitationnel, il subit deux types de mouvements :
• Dans l'axe vertical, il se déplace en raison de l'effet de la gravité, subissant une accélération gravitationnelle. Pour les trajectoires de faible hauteur, cette accélération peut être considérée comme constante.
• Dans l'axe horizontal, en supposant que la résistance de l'air soit négligeable, l'objet se déplace à une vitesse constante car il n'y a pas de force pour l'accélérer ou le freiner.
Le résultat est ce que l'on appelle une trajectoire balistique, qui atteint sa portée maximale lorsqu'elle est lancée ou tirée sous un angle de 45 degrés.
ID:(1446, 0)
Trajectoire balistique
Description
Si un objet est lancé ou tiré dans un champ gravitationnel, il subit deux types de mouvements : • Dans l'axe vertical, il se déplace en raison de l'effet de la gravité, subissant une accélération gravitationnelle. Pour les trajectoires de faible hauteur, cette accélération peut être considérée comme constante. • Dans l'axe horizontal, en supposant que la résistance de l'air soit négligeable, l'objet se déplace à une vitesse constante car il n'y a pas de force pour l'accélérer ou le freiner. Le résultat est ce que l'on appelle une trajectoire balistique, qui atteint sa portée maximale lorsqu'elle est lancée ou tirée sous un angle de 45 degrés.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
A position ($s$) parcouru avec ERROR:8173,0 avec a vitesse ($s_0$), le temps ($t$) et le temps initial ($t_0$) est
Par cons quent, si le mouvement d marre l'origine ($s_0=0$) au d but du temps ($t_0=0$), le mouvement est d crit par $x=s$ et $v_0=v_{0x}$.
(ID 10930)
Pour le cas o ERROR:5297,0 est gal l'acc l ration gravitationnelle ($a_0=-g$), la trajectoire verticale peut tre calcul e en utilisant l' quation pour a position ($s$) avec a vitesse ($s_0$), a vitesse initiale ($v_0$), le temps ($t$) et le temps initial ($t_0$) :
Dans le sc nario o le mouvement d marre a hauteur à laquelle tirer ($h$) ($s_0=h$), le temps initial ($t_0$) ($t_0=0$) et a vitesse verticale initiale ($v_{0y}$) ($v_0=v_{0y}$) sont donn s, le mouvement peut tre d crit par la formule :
(ID 10931)
Pour d terminer le temps d'impact, nous pouvons utiliser l' quation de a position sur l'axe y ($y$), qui d pend de a hauteur à laquelle tirer ($h$), a vitesse verticale initiale ($v_{0y}$), a accélération gravitationnelle ($g$) et le temps ($t$), o la hauteur est nulle :
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
Cela donne un temps :
$t=\displaystyle\frac{ v_{y0} +\sqrt{ v_{0y} ^2 + 2 g h }}{g}$
Avec a vitesse initiale ($v_0$) et le hauteur maximale atteinte ($\phi$) :
| $ v_{0y} = v_0 \sin \phi $ |
a temps d'impact ($t_{imp}$) est :
| $ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$ |
(ID 10934)
Puisque a temps d'impact ($t_{imp}$) avec a vitesse initiale ($v_0$), le hauteur maximale atteinte ($\phi$), a accélération gravitationnelle ($g$) et a hauteur à laquelle tirer ($h$) est
| $ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$ |
alors a position sur l'axe des x ($x$) avec a vitesse horizontale initiale ($v_{0x}$) et le temps ($t$)
| $ x = v_{0x} t $ |
et a vitesse horizontale initiale ($v_{0x}$) avec a vitesse initiale ($v_0$) et le hauteur maximale atteinte ($\phi$)
| $ v_{0x} = v_0 \cos \phi $ |
nous avons donc
| $ x_{imp} =\displaystyle\frac{ v_0 ^2\sin \phi \cos \phi }{ g }\left(1 + \sqrt{1 + \displaystyle\frac{2 g h }{ v_0 ^2\sin^2 \phi }}\right)$ |
(ID 10935)
A temps de la hauteur maximale ($t_{max}$) est atteint lorsque a position sur l'axe y ($y$) atteint une valeur maximale. Cette hauteur peut tre calcul e avec a hauteur à laquelle tirer ($h$), a vitesse verticale initiale ($v_{0y}$), a accélération gravitationnelle ($g$) et le temps ($t$),
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
dont la d riv e par rapport au temps est nulle au maximum, ce qui implique :
$\displaystyle\frac{dy}{dt}=v_{0,y}-gt=0$
Ainsi, avec l'expression pour a vitesse initiale ($v_0$),
| $ v_{0y} = v_0 \sin \phi $ |
nous avons que
| $ t_{max} =\displaystyle\frac{ v_0 }{ g }\sin \phi $ |
(ID 10936)
Le hauteur maximale atteinte ($y_{max}$) est atteint en une temps de la hauteur maximale ($t_{max}$) avec le hauteur maximale atteinte ($\phi$), a vitesse constante ($v_0$) et a accélération gravitationnelle ($g$),
partir duquel nous pouvons d terminer a position sur l'axe y ($y$) avec a hauteur à laquelle tirer ($h$), a vitesse verticale initiale ($v_{0y}$) et le temps ($t$) en utilisant l' quation
Ainsi, avec a vitesse verticale initiale ($v_{0y}$),
le hauteur maximale atteinte ($y_{max}$), c'est
(ID 10937)
Exemples
(ID 15404)
Pendant le Moyen ge, lorsqu'on observait le vol d\'un boulet de canon, on dessinait une courbe qui montrait une mont e prononc e suivie d\'une chute presque verticale, comme on peut le voir sur l\'image :
Cependant, en analysant les quations de la cin matique, on sait que la trajectoire r elle du boulet de canon est tr s diff rente. En fait, il s\'agit d\'une parabole qui est produite par la combinaison du mouvement vertical, caus par la gravit , et du mouvement horizontal, qui est constant.
En d\'autres termes, le temps pendant lequel le boulet de canon reste en l\'air est d termin par son mouvement vertical, tandis que la distance parcourue dans la direction horizontale est d termin e par sa vitesse horizontale.
(ID 13996)
La trajectoire balistique suit g n ralement une parabole invers e avec un point de ERROR:8433,0 et une distance maximale atteinte ($x_{imp}$) avec a temps de la hauteur maximale ($t_{max}$) et a temps d'impact ($t_{imp}$) :
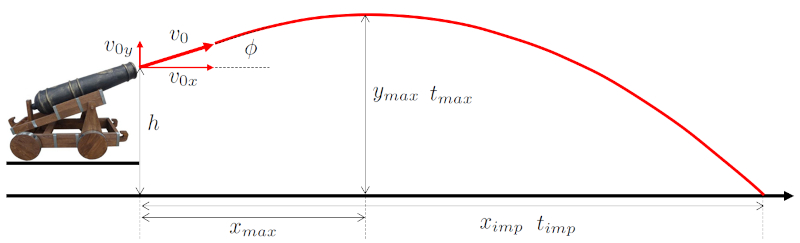
Remarque : Strictement parlant, les composantes doivent tre estim es en fonction de leurs valeurs au niveau du sol pour d terminer avec pr cision les param tres de la hauteur maximale et du point d'impact.
(ID 12536)
(ID 15407)
ID:(1446, 0)