Intercept at constant angular speed
Storyboard 
Objects can intersect when they coincide in angle at the same moment. To achieve this, they must move from their respective initial angles with angular velocities that allow them to coincide in angle and time at the end of the journey.
ID:(1450, 0)
Intercept at constant angular speed
Description 
Objects can intersect when they coincide in angle at the same moment. To achieve this, they must move from their respective initial angles with angular velocities that allow them to coincide in angle and time at the end of the journey.
Variables
Calculations
Calculations
Equations
In the case where the initial Angular Speed ($\omega_0$) is equal to the mean angular velocity ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Therefore, with the difference of Angles ($\Delta\theta$), which is equal to the angle ($\theta$) divided by the initial Angle ($\theta_0$), we obtain:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
And with the time elapsed ($\Delta t$), which is equal to the time ($t$) divided by the start Time ($t_0$), we obtain:
| $ \Delta t \equiv t - t_0 $ |
We can rewrite the equation for the mean angular velocity ($\bar{\omega}$) as:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
This can be expressed as:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Solving for it, we get:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
In the case where the initial Angular Speed ($\omega_0$) is equal to the mean angular velocity ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Therefore, with the difference of Angles ($\Delta\theta$), which is equal to the angle ($\theta$) divided by the initial Angle ($\theta_0$), we obtain:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
And with the time elapsed ($\Delta t$), which is equal to the time ($t$) divided by the start Time ($t_0$), we obtain:
| $ \Delta t \equiv t - t_0 $ |
We can rewrite the equation for the mean angular velocity ($\bar{\omega}$) as:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
This can be expressed as:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Solving for it, we get:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
| $ \Delta s=r \Delta\theta $ |
and the definition of the mean angular velocity ($\bar{\omega}$) is
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
| $ v = r \omega $ |
.
(ID 3233)
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
| $ \Delta s=r \Delta\theta $ |
and the definition of the mean angular velocity ($\bar{\omega}$) is
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
| $ v = r \omega $ |
.
(ID 3233)
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
and the time elapsed ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
and the time elapsed ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Examples
(ID 15411)
In the case of an intersection, two bodies are moving in such a way that they will meet at ERROR:10307,0 at time a intersection time ($t$).
To achieve this, each body:
• Begins its displacement at the initial time of first object ($t_1$) at the initial angle of the first body ($\theta_1$) with a angular velocity of body 1 ($\omega_1$).
• Begins its displacement at the initial time of second object ($t_2$) at the initial angle of the second body ($\theta_2$) with a angular velocity of body 2 ($\omega_2$).
These conditions must be met to achieve the intersection.
Thus, the angle over time diagrams can be overlaid as shown in the following representation:
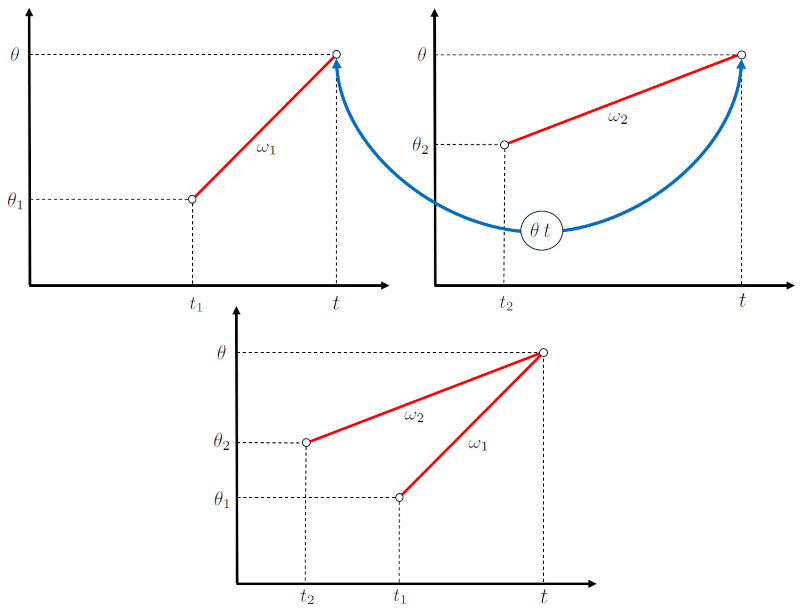
(ID 15517)
In the case of an intersection or collision between two objects, it's common for the angular velocity of body 1 ($\omega_1$) and the angular velocity of body 2 ($\omega_2$) to be configured such that they coincide.
This means that the angle traveled by the first body ($\Delta\theta_1$) and the travel time of first object ($\Delta t_1$) must result in a angular velocity of body 1 ($\omega_1$),
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
so that, with the angle traveled by the second body ($\Delta\theta_2$) and the travel time of second object ($\Delta t_2$), we get a angular velocity of body 2 ($\omega_2$),
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
so that they finally coincide in time and space (position):

(ID 15516)
In the case of a movement where two objects intersect, such as the angle of intersection ($\theta$) and the intersection time ($t$), it is common for both. Therefore, if for the first object, the initial time of first object ($t_1$) and the initial angle of the first body ($\theta_1$) with the angular velocity of body 1 ($\omega_1$) fulfill:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
and for the second object, the initial time of second object ($t_2$) and the initial angle of the second body ($\theta_2$) with the angular velocity of body 2 ($\omega_2$) fulfill:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
which is represented as:

(ID 15518)
(ID 15422)
ID:(1450, 0)
