Usuario:
Efecto de la Viscosidad
Descripción 
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Si consideramos el perfil de ERROR:5449,0 de un fluido en un canal cil ndrico, donde la velocidad en un radio del cilindro ($v$) var a en funci n de ERROR:10120,0 de acuerdo con la siguiente expresi n:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
con el radio del tubo ($R$) y la velocidad máxima del flujo ($v_{max}$). Podemos calcular la velocidad máxima del flujo ($v_{max}$) utilizando la viscosidad ($\eta$), la diferencia de presión ($\Delta p$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Si integramos la velocidad en toda la secci n transversal del canal, obtendremos el flujo de volumen ($J_V$), definida como la integral de $\pi r v(r)$ con respecto a ERROR:10120,0 desde $0$ hasta ERROR:5417,0. Esta integral se simplifica de la siguiente manera:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
La integraci n nos lleva a la ley de Hagen-Poiseuille resultante:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
Como
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
y las superficies paralelas ($S$) es
$S=2\pi r \Delta L$
donde el radio de la posición en un tubo ($r$) y el largo de tubo ($\Delta L$), con lo que la la fuerza de resistencia en cilindro ($F_v$) es
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
donde la viscosidad ($\eta$), la variación de la velocidad entre dos radios ($dv$) y el variación del radio en un tubo ($dr$).
(ID 3623)
La diferencia de presión ($\Delta p_s$) sobre una secci n de rea $\pi R^2$, con el radio del tubo ($R$) como el radio de la curvatura ($r$), genera una fuerza que se representa como:
$\pi r^2 \Delta p$
Esta fuerza impulsa el l quido en contra de la resistencia viscosa, que est dada por:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Igualando estas dos fuerzas, obtenemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Lo que nos lleva a la ecuaci n:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si integramos esta ecuaci n desde una posici n definida por el radio de la curvatura ($r$) hasta el borde donde el radio del tubo ($R$) (teniendo en cuenta que la velocidad en el borde es nula), podemos obtener la velocidad en un radio del cilindro ($v$) en funci n de el radio de la curvatura ($r$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Donde:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
es la la velocidad máxima del flujo ($v_{max}$) en el centro del flujo.
(ID 3627)
Ejemplos
Si se compara la viscosidad de la sangre medida con aquella estimada con la ecuaci n de Einstein se observa el siguiente comportamiento:
(ID 1694)
Cuando los gl bulos se adhieren a las paredes de los vasos tienden a enangostar el vaso. Este fen meno se denomina el efecto Fahraeus-Lindqvist y se muestra a continuaci n
Gl bulos adheridos a la pared
(ID 1896)
Efecto de la deformaci n de los hematocitos
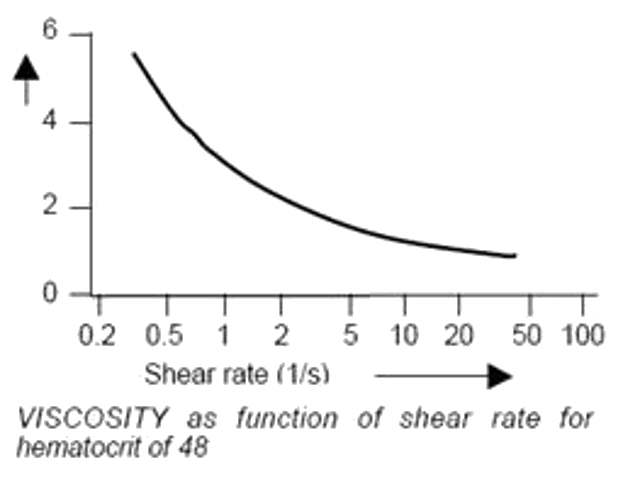
(ID 1895)
La deformaci n de los hematocitos lleva a que se vuelven mas hidrodin micos con lo que se reduce la resistencia.
(ID 1695)
ID:(328, 0)