Benützer:
Grundlagen der speziellen Relativitätstheorie
Storyboard 
Das Verhalten von Teilchen bei Geschwindigkeiten nahe der Lichtgeschwindigkeit unterscheidet sich von dem, was wir aus der klassischen Mechanik kennen. Deshalb müssen wir die Grundlagen der sogenannten speziellen Relativitätstheorie einführen, die Einstein zu Beginn des letzten Jahrhunderts formuliert hat.
ID:(1590, 0)
Zeitliche Dilatation: System in Ruhe
Bild
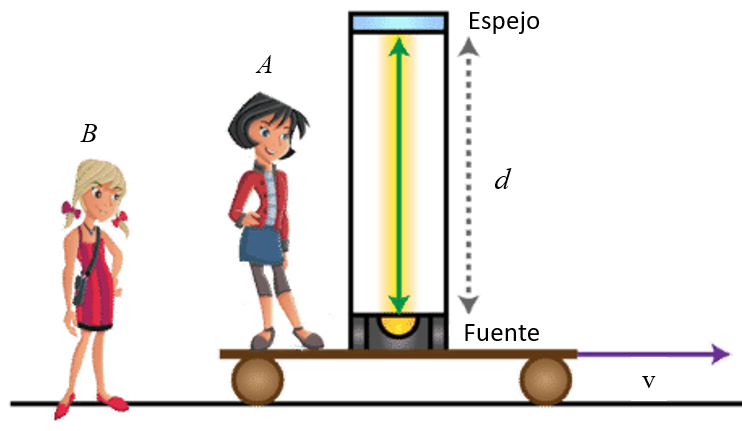
Betrachten wir ein System A, das sich horizontal mit einer Geschwindigkeit von $v$ bewegt, in dem sich ein Instrument befindet, das Licht vertikal aussendet. Dieses Licht wird nach der Reflexion an einem Spiegel zur Lichtquelle zurückkehrt:
ID:(11777, 0)
Zeitliche Dilatation: Ruhezeit
Gleichung
Angenommen, ein Photon wird ausgesandt, und wir messen die Zeit, die es benötigt, um von der Quelle zum Spiegel zu gelangen, die wir als $\Delta t_0$ bezeichnen. Wenn die Länge des Instruments $d$ beträgt und die Lichtgeschwindigkeit $c$ ist, dann beträgt die Gesamtzeit:
 $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
ID:(11778, 0)
Zeitliche Dilatation: Zeit in Bewegung
Bild
Für System A ist die Zeit, um die Strecke $d$ zurückzulegen, unabhängig davon, ob System A mit konstanter Geschwindigkeit $v$ in Bewegung ist, gleich $\Delta t_0$:
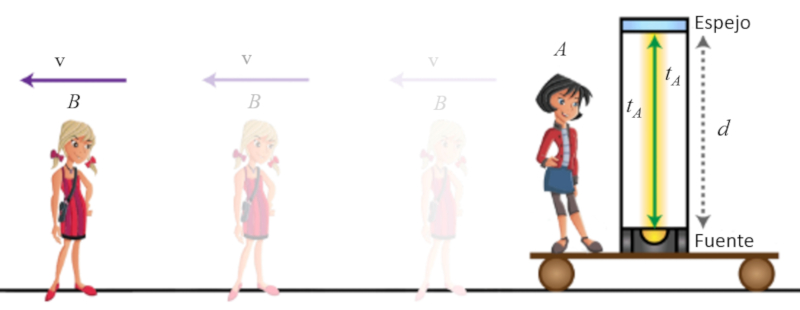
Dies liegt daran, dass das Konzept der Bewegung relativ ist und immer auf eine Geschwindigkeit bezogen werden sollte, die sich auf ein bestimmtes System bezieht. In diesem Fall beobachtet System B System A und behauptet, dass A sich mit einer Geschwindigkeit von $v$ bewegt. Allerdings könnte man genauso gut aus der Perspektive von A behaupten, dass A ruht und dass es tatsächlich System B ist, das sich mit einer Geschwindigkeit von $-v$ bewegt.
ID:(11779, 0)
Zeitdilatation: von einem System in Ruhe
Bild
Wenn es aus einem System B betrachtet wird, das sich im Vergleich zum System A im Ruhezustand befindet, wird die Zeit als $\Delta t_v$ geschätzt:
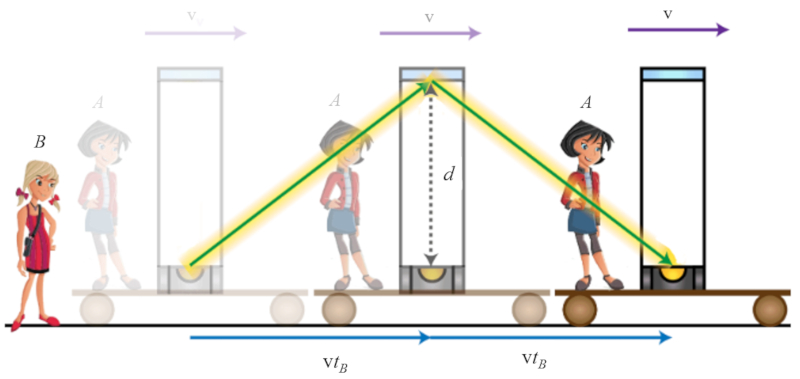
Aus der Sicht von B umfasst der Weg, den das Photon zurücklegt, nicht nur die vertikale Strecke $d$, sondern auch einen zusätzlichen horizontalen Weg von $v \Delta t_v$.
ID:(11780, 0)
Zeitdilatation: Zeit von einem System in Ruhe
Gleichung
Aus der Perspektive des Systems B kann die zurückgelegte Strecke mit dem Satz des Pythagoras berechnet werden, wobei der horizontale Weg als $v \Delta t_v$ und der vertikale Weg als $d$ berücksichtigt werden:
$(v \Delta t_v)^2+d^2=(c \ Delta t_v)^2$
Daher wird die Zeit aus der Sicht von B wie folgt berechnet:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
ID:(11781, 0)
Zeitdilatation
Gleichung
Da der Abstand $d$ orthogonal zur Verschiebung steht, bleibt er unabhängig von der horizontalen Verschiebung gleich, was in den Zeiten von A:
| $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
und B:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
resultiert. Daher können wir schlussfolgern, dass:
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
Es folgt, dass ein
gleiches Ereignis je nach Beobachtung aus einem System, in dem das Ereignis ruht, oder einem, das sich bewegt, eine unterschiedliche Dauer hat.
Dieses Phänomen veranschaulicht das Konzept der
Zeitdilatation, bei der die wahrgenommene Zeit je nach der relativen Geschwindigkeit zwischen den Beobachtern variiert.
ID:(11782, 0)
Zeitliche Dilatation mit dem Lorentz-Faktor
Gleichung
Die zeitliche Dilatation, berechnet mit der Gleichung
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
kann äquivalent ausgedrückt werden als
| $ \gamma =\displaystyle\frac{1}{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
auf folgende Weise:
| $ \Delta t_v = \gamma \Delta t_0 $ |
ID:(11784, 0)
Distanzkontraktion
Bild
Die Zeitdilatation, zusammen mit der Bedingung, dass in allen Systemen die Lichtgeschwindigkeit konstant bleibt, führt zur Notwendigkeit einer Längenkontraktion.
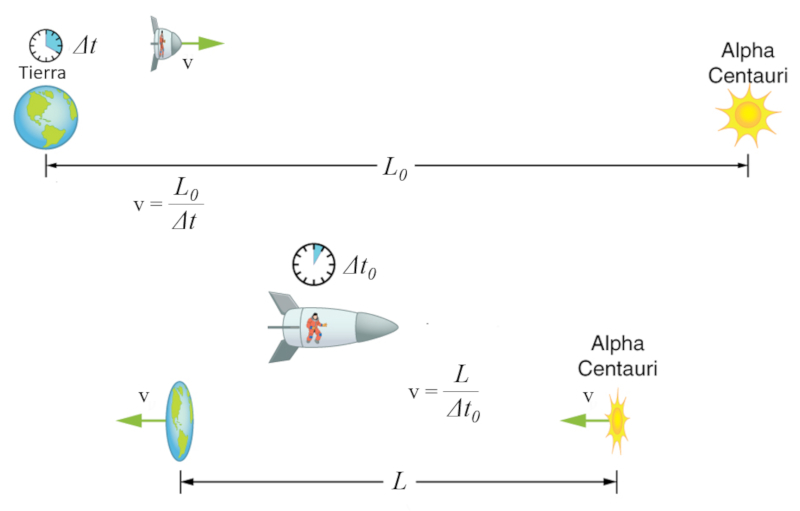
ID:(11785, 0)
Kontraktion von Distanzen, Beziehung
Gleichung
Im System B entspricht die Strecke, die das bewegte System A zurücklegt, genau $L_0$ bei einer Geschwindigkeit von:
$v=\displaystyle\frac{ L_0 }{ \Delta t_v }$
Aus der Perspektive des Systems A wird die zurückgelegte Strecke als $L_v$ innerhalb einer Zeitspanne von $\Delta t_0$ mit einer Geschwindigkeit von:
$v=\displaystyle\frac{ L_v }{ \Delta t_0 }$
Daher beobachten wir aufgrund der beschriebenen Zeitdilatation
| $ \Delta t_v = \gamma \Delta t_0 $ |
eine räumliche Kontraktion wie
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
ID:(11786, 0)