User:


Electric field
Storyboard

As loads generate forces, a load distribution will act on a load that positions one at any point in space. In other words there is a 'field' that is a force at any point in space. This force depends on the charge we expose, so it makes sense to define a force per charge so that it is independent of the particle's charge that we seek to study its behavior. Therefore it is possible to define what we call an electric field that is the total sum of all Coulomb forces of the distributed charges divided by the charge of the particle from which the behavior is being studied.

>Model

ID:(814, 0)


Electric field
Description

>Top


Electric charges generate electric fields that in turn are capable of affecting their behavior. In other words, we are studying the system, affecting its behavior with our intervention. If I measure Coulomb's strength

$ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$



with it includes a q load to study how Q works.

ID:(790, 0)


Electric field
Equation

>Top, >Model


If I want to study the system without the q test load that I am using to measure, such as Coulomb force

$ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$



I must separate what is the test load from the rest that we will call the electric field \vec{E}.

The electric field generates \vec{E} a force \vec{F} on a q charge that acts in the same direction as this. So with you have

$ F = q E $

ID:(3872, 0)


Test Charge
Equation

>Top, >Model


To measure the strength of Coulomb it is required to introduce a test load into the system. If this load is q, the force per load that the system loads exert on the test load can be estimated. The force magnitude \vec{F} per charge q is called the electric field \vec{E} and is measured in Newton (N) by Coulomb (C). The electric field is measured assuming that the test load does not greatly disturb the system, in other words it is assumed to be very small and the field definition with can be written as

$ \vec{E} =\lim_{q\rightarrow 0}\displaystyle\frac{ \vec{F} }{ q }$

ID:(3724, 0)


Electric field of a point charge
Equation

>Top, >Model


With the Coulomb force of a charge with it is

$ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$



and the definition of the electric field with charge $C$, electric eield (vector) $V/m$ and force (vector) $N$ as

$ \vec{E} =\lim_{q\rightarrow 0}\displaystyle\frac{ \vec{F} }{ q }$



obtained with charge $C$, electric eield (vector) $V/m$ and force (vector) $N$

$ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$

ID:(11379, 0)


Electric field for various charges
Image

>Top


When there are several charges, multiple Coulomb forces must be added in order to obtain the total force:

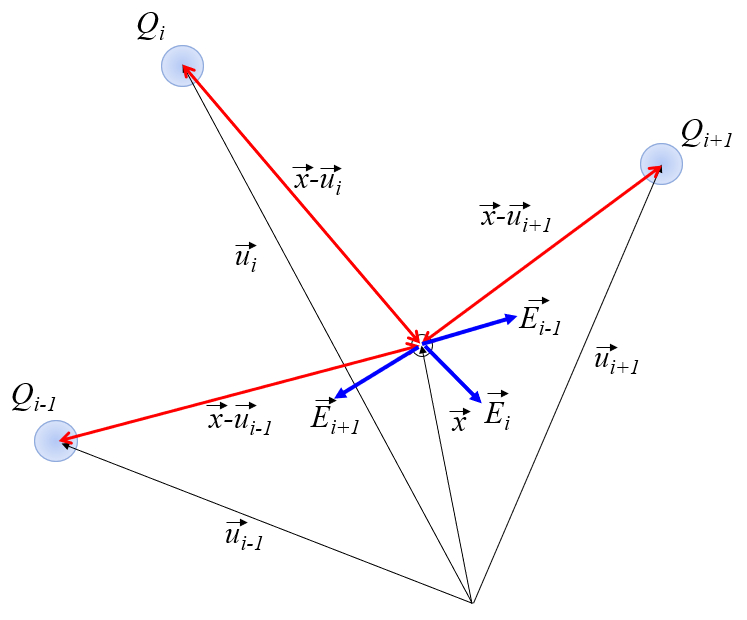
ID:(11378, 0)


Electric field distribution of charges
Equation

>Top, >Model


Si existen N cargas de magnitudes Q_i en posiciones \vec{u}_i, la fuerza de Coulomb con es

$ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$



que con la definición del campo eléctrico con charge $C$, electric eield (vector) $V/m$ and force (vector) $N$

$ \vec{E} =\lim_{q\rightarrow 0}\displaystyle\frac{ \vec{F} }{ q }$



se tiene que el campo eléctrico de una distribución de cargas con charge $C$, electric eield (vector) $V/m$ and force (vector) $N$ es

$ \vec{E} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_ i ^ N \displaystyle\frac{ Q_i }{| \vec{x} - \vec{u}_i |^3}( \vec{x} - \vec{u}_i )$

ID:(3726, 0)


0
Video

Video: Electric field