Deformação plástica
Storyboard 
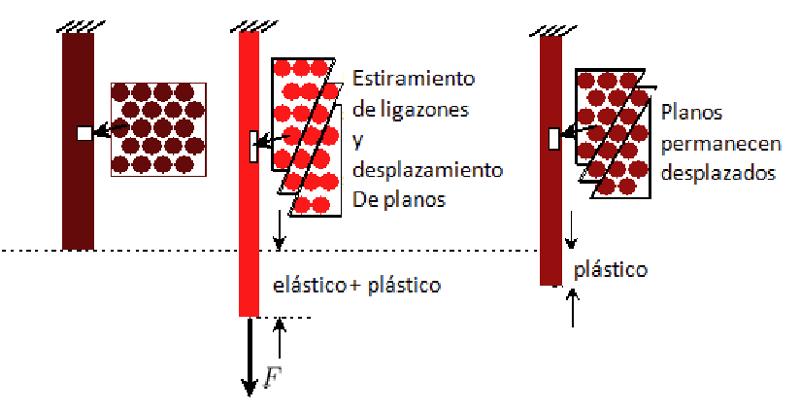
Para pequenas deformações, o material sofre apenas uma deformação elástica, ou seja, ao retirar a carga, ele retorna à sua forma original. Para deformações maiores, os átomos podem sofrer deslocamentos maiores, alterando permanentemente a estrutura. Nestes casos, falamos de deformação plástica.
ID:(324, 0)
Deformação plástica
Storyboard 
Para pequenas deformações, o material sofre apenas uma deformação elástica, ou seja, ao retirar a carga, ele retorna à sua forma original. Para deformações maiores, os átomos podem sofrer deslocamentos maiores, alterando permanentemente a estrutura. Nestes casos, falamos de deformação plástica.
Variáveis
Cálculos
Cálculos
Equações
Exemplos
O osso pode ser modelado como um cilindro oco, pois o material em seu interior n o capaz de suportar uma carga significativa. Portanto, ele modelado geometricamente como um cilindro com propriedades o comprimento do corpo ($L$), o raio interno ($R_1$) e o rádio externa ($R_2$):
Portanto, o raio efetivo ($R$)
la seção de elemento ($S$)
e o momento de inércia da superfície ($I_s$)
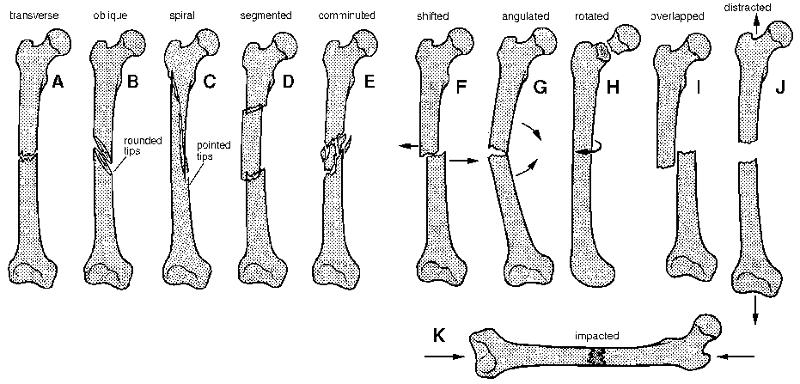
No caso do osso, existem diferentes situa es que levam gera o de tens es extremas que resultam em fraturas.
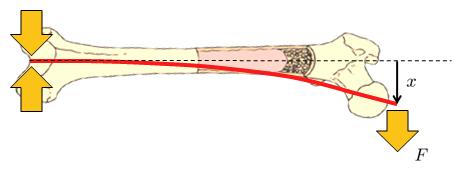
Uma situa o quando o osso est fixo em uma extremidade e flexionado a partir da outra:
Um exemplo uma pessoa caindo e apoiando-se em um ponto, criando um ponto fixo por atrito enquanto o centro de massa continua se movendo devido in rcia, flexionando o osso at que ele frature.
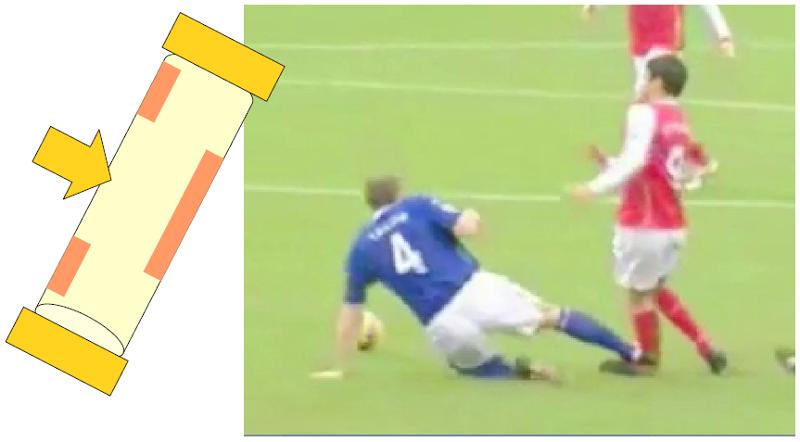
Outra situa o quando est fixo em ambas as extremidades e recebe uma for a perpendicular em alguma posi o intermedi ria:
Um exemplo t pico disso quando um jogador de futebol coloca o p (um ponto fixo) e a massa de seu corpo, devido in rcia, ret m o segundo ponto, que pode ser considerado fixo, enquanto outro jogador impacta sua perna com o p .
Por ltimo, h a situa o em que o osso entra em colapso devido press o axial.
Nesse caso, existem duas situa es. Por um lado, a estrutura do pr prio osso pode entrar em colapso e fraturar devido compress o. Por outro lado, pode haver flambagem, o que significa que, devido a alguma heterogeneidade, o osso se flexiona e acaba se desviando de forma extrema, levando fratura.
Esses s o os mecanismos b sicos que posteriormente, na realidade, podem iniciar o processo, comprometendo outros ossos ou se estendendo dentro do mesmo osso, resultando em uma fratura mais complexa.
Uma situa o que pode ocorrer quando uma força de deformação com ponto fixo ($F_1$) age sobre um osso com as propriedades um comprimento do corpo ($L$), o módulo de Elasticidade ($E$) e o momento de inércia da superfície ($I_s$), que est fixo em uma extremidade.
la energia de deformação com ponto fixo ($W_1$), que armazena a estrutura contra uma tensão à deformação com um ponto fixo ($\sigma_1$), definido por
la força de deformação com ponto fixo ($F_1$), a for a aplicada, leva a uma tensão à deformação com um ponto fixo ($\sigma_1$), conforme
e la tensão à deformação com um ponto fixo ($\sigma_1$), que depende de o rádio externa ($R_2$), dado por
Uma situa o que pode ocorrer quando uma força de deformação com dois pontos fixos ($F_2$) age sobre um osso com as propriedades um comprimento do corpo ($L$), o módulo de Elasticidade ($E$) e o momento de inércia da superfície ($I_s$), que est fixo em ambos os extremos:
la energia de deformação com dois pontos fixos ($W_2$), que armazena a estrutura contra um movimento em flexão com dois pontos fixos ($u_2$), dado por
la força de deformação com dois pontos fixos ($F_2$), a for a aplicada, leva a um movimento em flexão com dois pontos fixos ($u_2$) conforme
e la tensão à deformação com dois pontos fixos ($\sigma_2$), que depende de o rádio externa ($R_2$), expresso como
Um cen rio poss vel que uma força de deformação em condição de flambagem ($F_p$) atue ao longo do eixo do osso com as propriedades um comprimento do corpo ($L$), o módulo de Elasticidade ($E$), o fator de flambagem ($K$), o raio efetivo ($R$) e o momento de inércia da superfície ($I_s$), gerando flambagem:
la energia de deformação em condição de flambagem ($W_p$), definido como
la força de deformação em condição de flambagem ($F_p$), a for a aplicada, de acordo com
e la tensão à deformação em caso de flambagem ($\sigma_p$), que depende de o rádio externa ($R_2$), expresso como
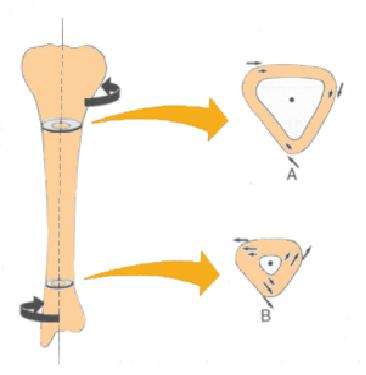
Uma forma de causar uma fratura atrav s da tor o do osso, o que envolve a aplica o de torques opostos nas extremidades:
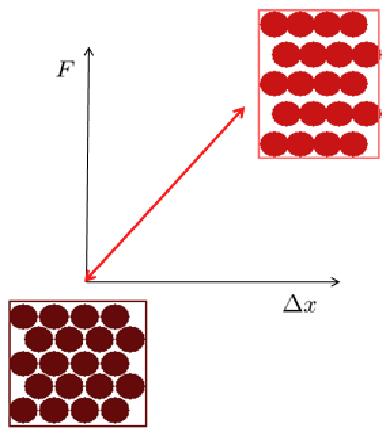
A deforma o el stica microsc pica corresponde a uma modifica o na dist ncia entre os tomos sob uma for a externa, sem qualquer rearranjo desses tomos.
Em geral, uma deforma o onde a dist ncia muda de forma proporcional for a aplicada, referida como deforma o el stica.
A deforma o pl stica significa que, se a tens o aplicada for reduzida, o material diminui sua deforma o, mas acaba com uma deforma o permanente.
Portanto, se for submetido novamente tens o, geralmente retorna sua forma el stica, mas devido nova forma, n o consegue recuperar sua forma original.
A deforma o pl stica envolve os tomos se reorganizando, dissociando-se das estruturas existentes e formando novas liga es que s o intrinsecamente est veis. No entanto, essa deforma o geralmente implica em uma modifica o na forma do material.
A deforma o pl stica pode eventualmente levar a altera es que podem incluir rupturas catastr ficas, que s o permanentes.
Trabalharemos com osso e com os cen rios de queda e impacto. Os par metros sseos e as propriedades do material est o resumidos aqui:
Se um jogador atingido no meio do osso e considera-se que o p , devido ao atrito, e o corpo, devido in rcia, s o pontos fixos, isso resulta em uma carga que flexiona o osso.
Pergunta de interesse: Qual a energia, a tens o, a for a, o deslocamento e a altura do salto nos quais ocorreria o pandeo? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
S o consideradas duas situa es, queda (quebra por flambagem, compress o ou flex o) e impacto na parte central do osso (quebra por flex o).
A integra o sobre a se o com o raio interno ($R_1$) e o rádio externa ($R_2$) leva introdu o de o raio efetivo ($R$), definido por:
Com o rádio externa ($R_2$) e o raio interno ($R_1$), la seção de elemento ($S$) definido por
O momento de inércia da superfície ($I_s$) calculado no caso de um cilindro com o rádio externa ($R_2$) e o raio interno ($R_1$) atrav s de
A rela o entre la energia de deformação com dois pontos fixos ($W_2$) e o movimento em flexão com dois pontos fixos ($u_2$) em uma flex o com dois pontos fixos depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$)
A rela o entre la força de deformação com dois pontos fixos ($F_2$) e o movimento em flexão com dois pontos fixos ($u_2$) em uma flex o com dois pontos fixos depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$). Neste contexto,
A rela o entre la tensão à deformação com dois pontos fixos ($\sigma_2$) e la força de deformação com dois pontos fixos ($F_2$) em uma flex o com dois pontos fixos depende de o rádio externa ($R_2$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$). Neste contexto,
A rela o entre la energia de deformação com ponto fixo ($W_1$) e o deslocamento de flexão com ponto fixo ($u_1$) em uma flex o com um ponto fixo depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$) :
A rela o entre la força de deformação com ponto fixo ($F_1$) e o deslocamento de flexão com ponto fixo ($u_1$) em uma flex o com um ponto fixo depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$) :
A rela o entre la tensão à deformação com um ponto fixo ($\sigma_1$) e la força de deformação com ponto fixo ($F_1$) em uma flex o com um ponto fixo depende de o rádio externa ($R_2$), o comprimento do corpo ($L$) e o momento de inércia da superfície ($I_s$) :
La energia de deformação em condição de flambagem ($W_p$) no encurvamento depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$), o momento de inércia da superfície ($I_s$), o raio efetivo ($R$) e o fator de flambagem ($K$)
O valor de o fator de flambagem ($K$) :
• 0,5 se ambas as bordas estiverem fixas,
• 1,0 se ambas puderem girar,
• 0,7 se uma estiver fixa e a outra puder girar, e
• 2,0 se ambas estiverem livres.
La força de deformação em condição de flambagem ($F_p$) no encurvamento depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$), o momento de inércia da superfície ($I_s$) e o fator de flambagem ($K$).
O valor de o fator de flambagem ($K$) :
• 0,5 se ambas as bordas estiverem fixas,
• 1,0 se ambas puderem girar,
• 0,7 se uma estiver fixa e a outra puder girar, e
• 2,0 se ambas estiverem livres.
La tensão à deformação em caso de flambagem ($\sigma_p$) no encurvamento depende de o módulo de Elasticidade ($E$), o comprimento do corpo ($L$), o momento de inércia da superfície ($I_s$), la seção de elemento ($S$) e o fator de flambagem ($K$).
O valor de o fator de flambagem ($K$) :
• 0,5 se ambas as bordas estiverem fixas,
• 1,0 se ambas puderem girar,
• 0,7 se uma estiver fixa e a outra puder girar, e
• 2,0 se ambas estiverem livres.
ID:(324, 0)