Déformation plastique
Storyboard 
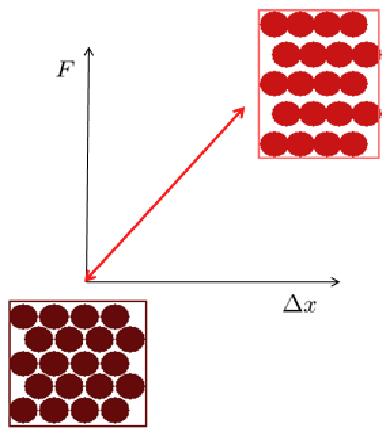
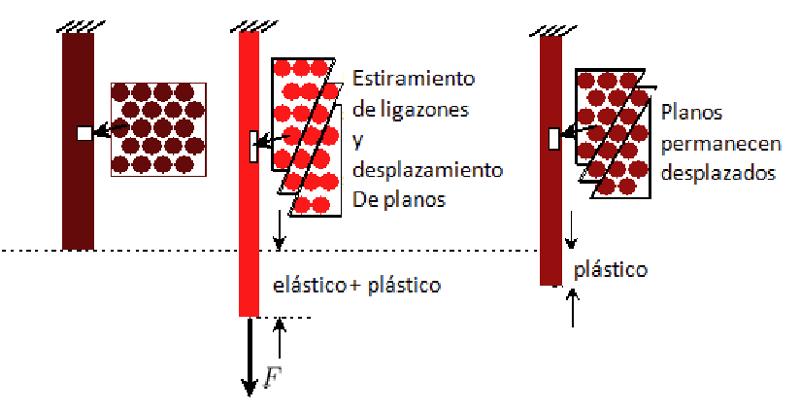
Pour de petites déformations, le matériau subit uniquement une déformation élastique, c'est-à-dire qu'après avoir retiré la charge, il retrouve sa forme d'origine. Pour des déformations plus importantes, les atomes peuvent subir des déplacements plus importants, modifiant la structure de manière permanente. Dans ces cas, nous parlons de déformation plastique.
ID:(324, 0)
Déformation plastique
Storyboard 
Pour de petites déformations, le matériau subit uniquement une déformation élastique, c'est-à-dire qu'après avoir retiré la charge, il retrouve sa forme d'origine. Pour des déformations plus importantes, les atomes peuvent subir des déplacements plus importants, modifiant la structure de manière permanente. Dans ces cas, nous parlons de déformation plastique.
Variables
Calculs
Calculs
Équations
Exemples
L'os peut tre mod lis comme un cylindre creux car le mat riau l'int rieur n'est pas capable de supporter une charge significative. Par cons quent, il est g om triquement repr sent par un cylindre avec les propri t s le la longueur du corps ($L$), le rayon intérieur ($R_1$) et le radio extérieure ($R_2$) :
Donc, le rayon effectif ($R$) est
a section d'élément ($S$) est
et le moment d'inertie superficiel ($I_s$) est
Dans le cas de l'os, il existe diff rentes situations qui conduisent la g n ration de tensions extr mes pouvant entra ner une fracture.
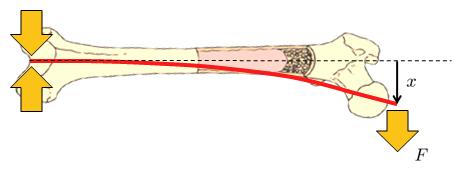
Une situation est lorsque l'os est fix une extr mit et est fl chi depuis l'autre :
Un exemple est une personne qui tombe et se soutient sur un point, cr ant ainsi un point fixe par frottement tandis que le centre de masse continue de se d placer par inertie, fl chissant l'os jusqu' ce qu'il se fracture.
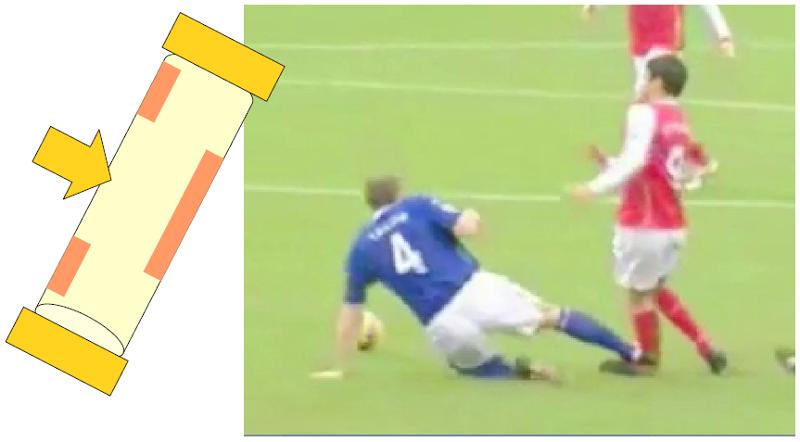
Une autre situation est lorsqu'il est fix aux deux extr mit s et re oit une force perpendiculaire une position interm diaire :
Un exemple typique est lorsqu'un joueur de football pose son pied (un point fixe) et que la masse de son corps, due l'inertie, retient le deuxi me point, qui peut tre consid r comme fixe, tandis qu'un autre joueur impacte sa jambe avec son pied.
Enfin, il y a la situation o l'os s'effondre sous l'effet d'une pression axiale.
Dans ce cas, il y a deux situations. D'une part, la structure m me de l'os peut s'effondrer et se fracturer sous l'effet de la compression. D'autre part, il peut y avoir du flambage, ce qui signifie qu'en raison d'une certaine inhomog n it , l'os se plie et finit par se d vier de mani re extr me, entra nant une fracture.
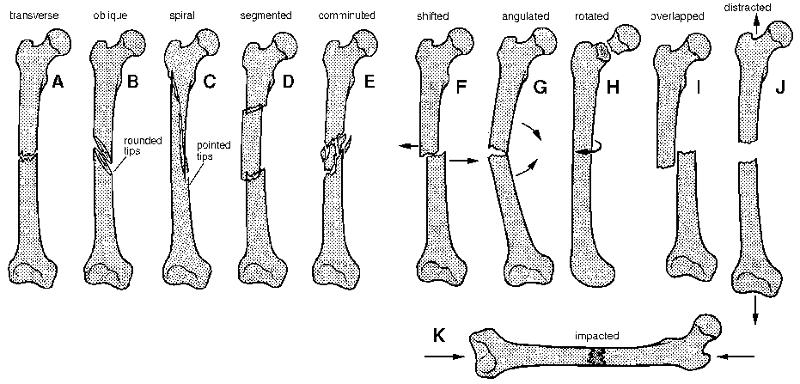
Ce sont les m canismes de base qui peuvent ensuite, dans la r alit , initier le processus, compromettre d'autres os ou se propager l'int rieur du m me os, entra nant une fracture plus complexe.
Une situation qui peut se produire est lorsque une force de déformation à point fixe ($F_1$) agit sur un os avec les propri t s un la longueur du corps ($L$), le module d'élasticité ($E$) et le moment d'inertie superficiel ($I_s$), qui est fix une extr mit .
a énergie de déformation avec un point fixe ($W_1$), qui stocke la structure contre une contrainte à la déformation avec un point fixe ($\sigma_1$), est d fini par
a force de déformation à point fixe ($F_1$), la force appliqu e, conduit une contrainte à la déformation avec un point fixe ($\sigma_1$) selon
et a contrainte à la déformation avec un point fixe ($\sigma_1$), qui d pend de le radio extérieure ($R_2$), est donn par
Une situation possible est que une force de déformation à deux points fixes ($F_2$) agisse sur un os avec les propri t s un la longueur du corps ($L$), le module d'élasticité ($E$) et le moment d'inertie superficiel ($I_s$), qui est fix aux deux extr mit s :
a énergie de déformation avec deux points fixes ($W_2$), qui stocke la structure contre un mouvement en flexion avec deux points fixes ($u_2$), est donn par
a force de déformation à deux points fixes ($F_2$), la force appliqu e, conduit un mouvement en flexion avec deux points fixes ($u_2$) selon
et a contrainte à la déformation avec deux points fixes ($\sigma_2$), qui d pend de le radio extérieure ($R_2$), est exprim comme
Un sc nario possible est que une force de déformation en condition de flambage ($F_p$) agisse le long de l'axe de l'os avec les propri t s un la longueur du corps ($L$), le module d'élasticité ($E$), le facteur de flambage ($K$), le rayon effectif ($R$) et le moment d'inertie superficiel ($I_s$), induisant un flambage :
a énergie de déformation en condition de flambage ($W_p$) est d fini comme
a force de déformation en condition de flambage ($F_p$), la force appliqu e, selon
et a contrainte à la déformation en cas de flambage ($\sigma_p$), qui d pend de le radio extérieure ($R_2$), est exprim comme
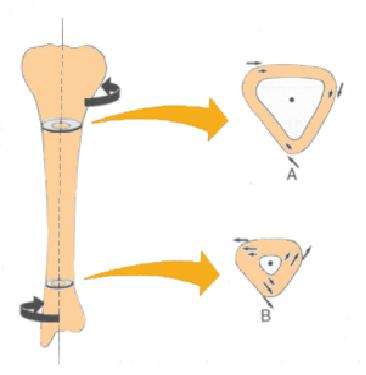
Une fa on de causer une fracture est travers la torsion osseuse, qui implique l'application de couples oppos s aux extr mit s :
La d formation lastique microscopique correspond une modification de la distance entre les atomes sous l'effet d'une force externe, sans qu'il y ait de r arrangement de ces atomes.
En g n ral, il s'agit d'une d formation o la distance change de mani re proportionnelle la force appliqu e, appel e d formation lastique.
La d formation plastique signifie que si la contrainte appliqu e est r duite, le mat riau diminue sa d formation mais finit par avoir une d formation permanente.
Par cons quent, s'il est soumis nouveau une contrainte, il revient g n ralement sa forme lastique, mais en raison de la nouvelle forme, il ne peut pas retrouver sa forme d'origine.
La d formation plastique implique que les atomes se r organisent, se dissociant des structures existantes et formant de nouvelles liaisons qui sont intrins quement stables. Cependant, cette d formation implique g n ralement une modification de la forme du mat riau.
La d formation plastique peut ventuellement entra ner des modifications qui peuvent inclure des ruptures catastrophiques, qui sont permanentes.
Nous travaillerons avec un os et avec les sc narios de chute et d'impact. Les param tres osseux et les propri t s des mat riaux sont r sum s icixa0:
Si un joueur est impact au milieu de l'os et que l'on consid re que le pied, en raison du frottement, et le corps, en raison de l'inertie, sont des points fixes, cela entra ne une charge qui fl chit l'os.
Question d'int r t : Quelle est l' nergie, la tension, la force, le d placement et la hauteur de saut auxquels surviendrait le flambage ? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
Deux situations sont consid r es, la chute (cassure due au flambage, la compression ou la flexion) et le choc sur la partie centrale de l'os (cassure due la flexion).
L'int gration sur la section avec le rayon intérieur ($R_1$) et le radio extérieure ($R_2$) conduit l'introduction de le rayon effectif ($R$), d fini par :
Avec le radio extérieure ($R_2$) et le rayon intérieur ($R_1$), a section d'élément ($S$) est d fini par
Le moment d'inertie superficiel ($I_s$) est calcul dans le cas d'un cylindre avec le radio extérieure ($R_2$) et le rayon intérieur ($R_1$) gr ce
La relation entre a énergie de déformation avec deux points fixes ($W_2$) et le mouvement en flexion avec deux points fixes ($u_2$) dans une flexion avec deux points fixes d pend de le module d'élasticité ($E$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$) est
La relation entre a force de déformation à deux points fixes ($F_2$) et le mouvement en flexion avec deux points fixes ($u_2$) dans une flexion avec deux points fixes d pend de le module d'élasticité ($E$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$). Dans ce contexte,
La relation entre a contrainte à la déformation avec deux points fixes ($\sigma_2$) et a force de déformation à deux points fixes ($F_2$) dans une flexion avec deux points fixes d pend de le radio extérieure ($R_2$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$). Dans ce contexte,
La relation entre a énergie de déformation avec un point fixe ($W_1$) et le déplacement en flexion avec un point fixe ($u_1$) dans une flexion avec un point fixe d pend de le module d'élasticité ($E$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$) est :
La relation entre a force de déformation à point fixe ($F_1$) et le déplacement en flexion avec un point fixe ($u_1$) dans une flexion avec un point fixe d pend de le module d'élasticité ($E$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$) est :
La relation entre a contrainte à la déformation avec un point fixe ($\sigma_1$) et a force de déformation à point fixe ($F_1$) dans une flexion avec un point fixe d pend de le radio extérieure ($R_2$), le la longueur du corps ($L$) et le moment d'inertie superficiel ($I_s$) est :
A énergie de déformation en condition de flambage ($W_p$) en flambage d pend de le module d'élasticité ($E$), le la longueur du corps ($L$), le moment d'inertie superficiel ($I_s$), le rayon effectif ($R$) et le facteur de flambage ($K$) est
La valeur de le facteur de flambage ($K$) est :
• 0,5 si les deux bords sont fixes,
• 1,0 si les deux peuvent tourner,
• 0,7 si l'un est fixe et l'autre peut tourner, et
• 2,0 si les deux sont libres.
A force de déformation en condition de flambage ($F_p$) en flambage d pend de le module d'élasticité ($E$), le la longueur du corps ($L$), le moment d'inertie superficiel ($I_s$) et le facteur de flambage ($K$).
La valeur de le facteur de flambage ($K$) est :
• 0,5 si les deux bords sont fixes,
• 1,0 si les deux peuvent tourner,
• 0,7 si l'un est fixe et l'autre peut tourner, et
• 2,0 si les deux sont libres.
A contrainte à la déformation en cas de flambage ($\sigma_p$) en flambage d pend de le module d'élasticité ($E$), le la longueur du corps ($L$), le moment d'inertie superficiel ($I_s$), a section d'élément ($S$) et le facteur de flambage ($K$).
La valeur de le facteur de flambage ($K$) est :
• 0,5 si les deux bords sont fixes,
• 1,0 si les deux peuvent tourner,
• 0,7 si l'un est fixe et l'autre peut tourner, et
• 2,0 si les deux sont libres.
ID:(324, 0)