Stall-Effekt
Storyboard 
Wenn der Anstellwinkel sehr groß ist, neigen die Whirlpools, die sich im oberen hinteren Teil des Flügels bilden, dazu, sich vorwärts zu bewegen, bis sie die Oberkante am Anfang des Flügels erreichen und den gesamten oberen Teil mit Whirlpools bedecken. In diesem Zustand senkt sich der Auftrieb dramatisch und erzeugt den sogenannten Stall-Effekt, der zu einem unkontrollierten Sturz des Objekts (Flugzeug / Vogel) führen kann.
Es gibt Situationen, in denen sowohl Flugzeuge als auch Vögel diesen Effekt genutzt haben, um Überraschungsangriffe aus großer Höhe auszuführen und eine Technik zu entwickeln, die den Flug kontrolliert und nicht auf dem Boden abstürzt.
ID:(1462, 0)
Stall-Effekt
Storyboard 
Wenn der Anstellwinkel sehr groß ist, neigen die Whirlpools, die sich im oberen hinteren Teil des Flügels bilden, dazu, sich vorwärts zu bewegen, bis sie die Oberkante am Anfang des Flügels erreichen und den gesamten oberen Teil mit Whirlpools bedecken. In diesem Zustand senkt sich der Auftrieb dramatisch und erzeugt den sogenannten Stall-Effekt, der zu einem unkontrollierten Sturz des Objekts (Flugzeug / Vogel) führen kann. Es gibt Situationen, in denen sowohl Flugzeuge als auch Vögel diesen Effekt genutzt haben, um Überraschungsangriffe aus großer Höhe auszuführen und eine Technik zu entwickeln, die den Flug kontrolliert und nicht auf dem Boden abstürzt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
Die Auftriebskraft ($F_L$) zusammen mit die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wird durch
repr sentiert, was zusammen mit die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) gleich sein muss:
das hei t:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
daraus ergibt sich:
Der Koeffizient Fahrstuhl ($C_L$) wird wie folgt mit die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$), die Oberfläche, die Auftrieb erzeugt ($S_w$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) berechnet:
Daher, mit die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$) und der Anstellwinkel eines Flügels ($\alpha$),
erhalten wir
Beispiele
Der Auftriebsbeiwert ist eine Funktion des Anstellwinkels und folgt in der Regel dem in der folgenden Abbildung dargestellten Trend:
Im gezeigten Fall betr gt die Steigung ungef hr 1,5 pro 15 Grad, was 0,1 1/Grad oder 5,73 1/Radiant entspricht.
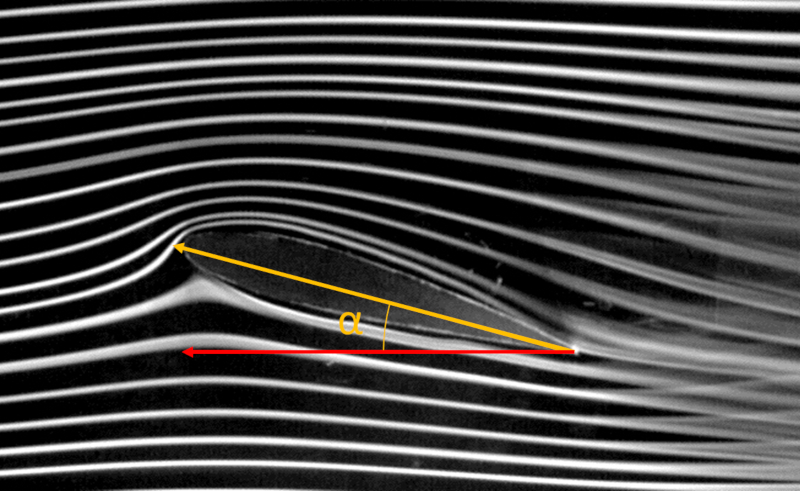
In einem Windkanalmodell eines Fl gels kann man beobachten, wie zu Beginn der Str mung laminar ist, aber sich zum Ende des Fl gels hin turbulente Str mung entwickelt:
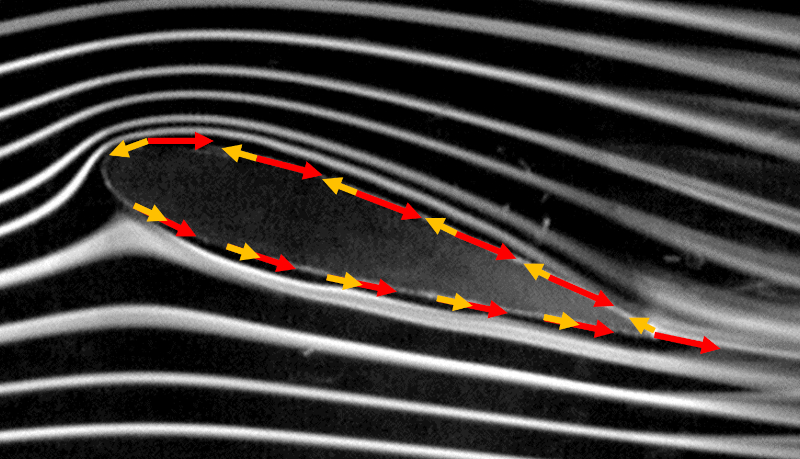
Wenn der Anstellwinkel einen kritischen Wert berschreitet (typischerweise zwischen 15 und 30 Grad, abh ngig von der Auslegung), wird die Oberfl che des Fl gels von Wirbeln bedeckt, und der Auftrieb f llt abrupt auf null.
An diesem Punkt tritt ein Ph nomen auf, das als Str mungsabriss (Stall) bekannt ist, bei dem die Luftstr mung ber dem Fl gel sich abl st und turbulente Wirbel entstehen. Diese Wirbel st ren die gleichm ige Luftstr mung erheblich, reduzieren den Auftrieb signifikant und beeintr chtigen die Steuerf higkeit des Flugzeugs. Es ist entscheidend, zu verhindern, dass der Anstellwinkel diesen kritischen Wert berschreitet, um einen stabilen und sicheren Flug aufrechtzuerhalten.
Wenn der Anstellwinkel einen kritischen Wert berschreitet (in der Regel zwischen 15 und 30 Grad, abh ngig von der Konstruktion), wird die Fl gelfl che von Wirbeln bedeckt und der Auftrieb f llt abrupt auf null.
An diesem Punkt tritt das Ph nomen des Str mungsabrisses (Stall) auf, bei dem der Luftstrom ber dem Fl gel abrei t und turbulente Wirbel entstehen. Diese Wirbel st ren den gleichm igen Luftstrom erheblich, verringern den Auftrieb drastisch und beeintr chtigen die Flugzeugsteuerung. Es ist wichtig, zu vermeiden, dass der Anstellwinkel diesen kritischen Wert berschreitet, um einen stabilen und sicheren Flug zu gew hrleisten.
Der Flug von National Airlines 102, einem Frachtflugzeug des Typs Boeing 747-400, das in Bagram, Afghanistan, startete, endete tragisch am 29. April 2013 aufgrund einer Verschiebung der Ladung w hrend des Starts. Die Verschiebung der Ladung f hrte zu einem Anstieg des Anstellwinkels, was zum Verlust des Auftriebs des Fl gels f hrte, ein Ph nomen, das als Str mungsabriss bekannt ist. Zus tzlich besch digte die Ladungsverschiebung das hydraulische System der Heckrudern, was das Flugzeug unkontrollierbar machte. Bedauerlicherweise verloren alle 7 Besatzungsmitglieder sofort bei der Kollision ihr Leben.
Hier ist eine Simulation, die den tragischen Start zeigt: Simulation
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schlie lich den Wert Null. Dies liegt daran, dass ber diesem kritischen Winkel die Wirbel vollst ndig die obere Fl che des Fl gels bedecken und somit der Auftrieb verloren geht. Dieses Ph nomen wird als \"Str mungsabriss\" bezeichnet.
Die Bedingung f r das Erreichen des Fluges wird erf llt, wenn die Auftriebskraft ($F_L$) dem Gewicht des Flugzeugs oder Vogels entspricht, das aus die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) berechnet wird. Dies wird durch ausreichende Werte von ERROR:6110,0, die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$) erreicht, wobei letzterer Koeffizient der anpassbare Faktor ist. Im Fall von Flugzeugen k nnen Piloten den Wert von der Koeffizient Fahrstuhl ($C_L$) mithilfe von Klappen ndern, deren Wert folgende Bedingung erf llen muss:
Die Klappen werden durch ndern des Winkels eingestellt, den der Fl gel zur Flugrichtung bildet, bekannt als Anstellwinkel.
Da der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist, kann der erforderliche Winkel zur Erzeugung ausreichender Auftriebskraft bei einer gegebenen Geschwindigkeit $v$ berechnet werden:
wobei $m$ die Masse, $g$ die Erdbeschleunigung, $\rho$ die Dichte des Mediums, $S_w$ die Fl gelfl che und $c$ die Proportionalit tskonstante zwischen dem Auftriebskoeffizienten und dem Anstellwinkel sind.
ID:(1462, 0)