Método de Newton
Definición 
El método de Newton permite estimar la raiz de una ecuación cuando no es posible despejar la variable de interés.
Para que sea efectivo se requiere de tener una idea aproximada de donde se encuentra la raíz que se esta buscando. El algoritmo parte de dicho punto y se va acercando succesivamente al valor que corresponde a la raíz.
ID:(564, 0)
Cuando no se puede Despejar
Imagen 
En muchos casos el despejar de una variable en una ecuación puede no ser posible. En estos casos se puede recurrir a técnicas en que se calcula una solución aproximada. Estos métodos iteran para obtener la solución por lo que es posible calcular la solución con la exactitud que se necesite. Uno de estos método es el de Newton.
ID:(560, 0)
Función para determinar la Raíz
Nota 
Supongamos que se tiene una función
Si se busca despejar la variable
En otras palabras se busca un valor
Esto también se puede planear como encontrar la raíz de una función
es decir el
lo que se da cuando la curva
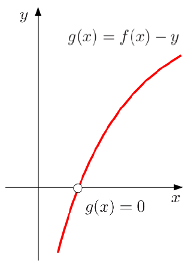
ID:(1875, 0)
Ejemplo: Ecuación
Video 
Un ejemplo simple es
Si calculamos la derivada empleando la definición tendremos que con
se obtiene
n el limite
Reemplazando esta expresión en la ecuación para iterar de Newton se obtiene
ID:(561, 0)
Método de Newton
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El m todo de Newton permite estimar la raiz de una ecuaci n cuando no es posible despejar la variable de inter s.
Para que sea efectivo se requiere de tener una idea aproximada de donde se encuentra la ra z que se esta buscando. El algoritmo parte de dicho punto y se va acercando succesivamente al valor que corresponde a la ra z.
(ID 564)
En muchos casos el despejar de una variable en una ecuaci n puede no ser posible. En estos casos se puede recurrir a t cnicas en que se calcula una soluci n aproximada. Estos m todos iteran para obtener la soluci n por lo que es posible calcular la soluci n con la exactitud que se necesite. Uno de estos m todo es el de Newton.
(ID 560)
Supongamos que se tiene una funci n
Si se busca despejar la variable
En otras palabras se busca un valor
Esto tambi n se puede planear como encontrar la ra z de una funci n
es decir el
lo que se da cuando la curva

(ID 1875)
Aproximaci n por una Recta
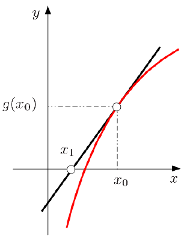
(ID 1876)
Primera Iteraci n
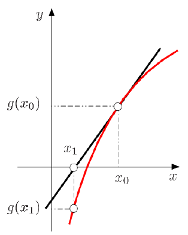
(ID 1879)
Constante de la Recta
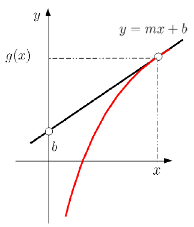
(ID 1878)
Pendiente de la Recta
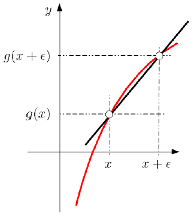
(ID 1877)
Segunda Iteraci n
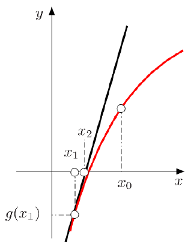
(ID 1880)
Ejemplo: c lculo
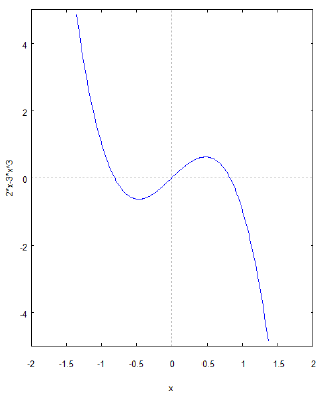
(ID 1881)
En general se puede continuar el proceso las veces que sea necesario para la exactitud que se necesite. En este proceso se calcula una aproximaci n
| $x_{n+1}=x_n-\displaystyle\frac{g(x_n)}{g_2(x_n)}$ |
(ID 3450)
Un ejemplo simple es
Si calculamos la derivada empleando la definici n tendremos que con
se obtiene
n el limite
Reemplazando esta expresi n en la ecuaci n para iterar de Newton se obtiene
(ID 561)
ID:(431, 0)
