Construcci n de diferenciales tanto exactos como inexactos en base a derivadas ordinarias y parciales.

(ID 565)

Funciones de dos Variables

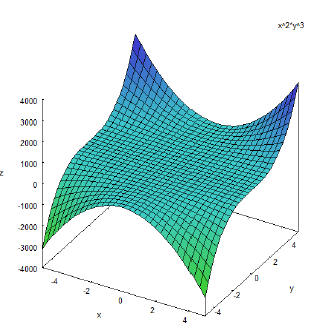
(ID 1882)

La diferencia en la variable x se refiere a la desviaci n del valor x respecto del valor de referencia x_0 y se escribe como

o en caso de ser una diferencia no infinitesimal

\Delta x=x-x_0

(ID 3463)

En general la derivada se puede empelar para establer relaciones de proprocinalidad.

Por ejemplo la variaci n del valor de la funci n f se puede escribir como df o \Delta f.

En forma an loga la variaci n de la variable x se puede llevar a escribir como dx o \Delta x.

Con ello, y empelando la derivada de f respecto de x en el punto x_0 se puede escribir la relaci n:

o en caso de ser una diferencia no infinitesimal

\Delta f=f'(x_0)\Delta x

(ID 3462)

Los polinomios se componen de suma de elementos del tipo x^n multiplicados por constantes.

Al ser la derivada lineal, la derivada de un polinomio es igual a la suma de los elementos derivados multiplicados por una constante.

Para calcular la derivada del factor x^n se puede empelar la definici n:

\displaystyle\frac{d}{dx}x^n=\lim_{\Delta x\rightarrow 0}\displaystyle\frac{(x+\Delta x)^n-x^n}{\Delta x}

Desarrollando el binomio se obtiene que

(x+\Delta x)^n=x^n+x^{n-1}\Delta x+\displaystyle\frac{1}{2}x^{n-2}\Delta x^2\ldots

con lo que en el limite que \Delta x es cero se obtiene

(ID 3456)

La diferencia en la variable y se refiere a la desviaci n del valor x respecto del valor de referencia y_0 y se escribe como

o en caso de ser una diferencia no infinitesimal

\Delta x=x-x_0

(ID 3466)

La diferencia en el valor de la funci n df se refiere a la desviaci n del valor f(x) respecto del valor de referencia f(x_0) y se escribe como

o en caso de ser una diferencia no infinitesimal

\Delta f=f(x)-f(x_0)

(ID 3464)

En general las derivadas parciales puede empelar para establer relaciones de proprocinalidad con funciones multivariables.

Por ejemplo la variaci n del valor de la funci n f se puede escribir como df o \Delta f.

En forma an loga la variaci n de la variable x se puede llevar a escribir como dx o \Delta x.

En forma an loga la variaci n de la variable y se puede llevar a escribir como dy o \Delta y.

Con ello, y empelando la derivada de f respecto de x en el punto x_0 y y en el punto y_0 se puede escribir la relaci n:

o en caso de ser una diferencia no infinitesimal

\Delta f=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y

(ID 3465)

En el caso de que la funci n depende de m s de una variable es necesario generalizar el concepto de derivada parcial.

La forma mas simple es continuar con la misma definici n anterior pero asumir que las demas variables se mantienen constantes.

A modo de ejemplo consideremos la funci n de dos variables $f(x,y)$. Supongamos que deseamos derivar respecto de $x$. El resultado puede variar si en el proceso de derivar el valor de $y$ se altera. Distinta es la situaci n si formzamos que $y$ se mantenga fijo $($constante$)$.

Para recordar que estamos realizando la derivada con la condici n de que las restantes variables no se alteran $($o sea $y$ permanece fijo$)$ empelamos una $d$ distinta: $\partial$ $($$\partial$ es una $d$ griega$)$.

Por ello en este caso pasaremos de

$\displaystyle\frac{df}{dx}\rightarrow\displaystyle\frac{\partial f}{\partial x}\equiv f_x$

o correspondientemente

$\displaystyle\frac{df}{dy}\rightarrow\displaystyle\frac{\partial f}{\partial y}\equiv f_y$

(ID 563)

Cuando escribimos el diferencial de la funci n f en dos dimensiones

no restringimos de ninguna forma como se lleva acabo la variaci n en los par metros x e y.

De hecho se asumi en que se puede variar x y luego y y que esto dar la misma variaci n df de que si variamos primero y y luego x.

Si dicha conmutatividad es aplicable hablamos de que df es un diferencial exacto.

Si el orden en que se realiza la variaci n no es arbitrario hablamos de un diferencial inexacto. Para diferenciarlo de un diferencial exacto empleamos la letra \delta. Si g fuera una funci n de este tipo el diferencial se escribir a como:

\delta g=g_x(x_0,y_0)dx+g_y(x_0,y_0)dy

(ID 3467)

Interpretaci n de Diferenciales Inexactos

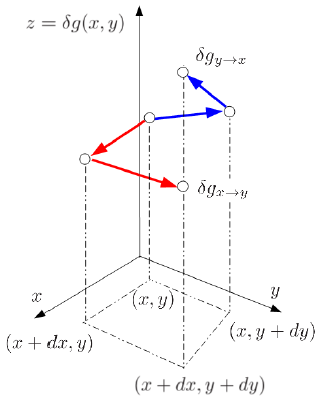
(ID 1883)