Usuario:


Compton Scattering
Definición

El scattering de Compton ocurre cuando un fotón interactua con una partícula cargada, en particular con un electrón. En el proceso el fotón pierde energía y se desvía poniendo el electrón en movimiento:

ID:(9176, 0)


Scattering
Imagen

Los scattering que contribuyen (in) o describen el abandono de partículas (out) se pueden graficar de la siguiente forma:

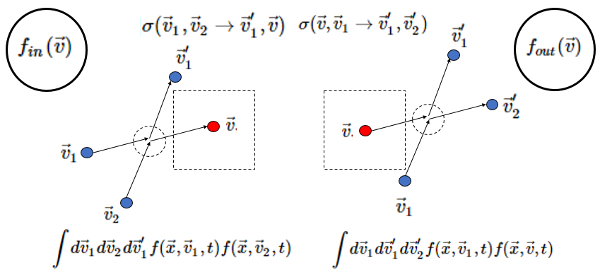
Gráfica Scattering entre dos partículas

Hay que notar que el termino colisión:

- integra sobre todas las velocidades externas a las del volumen

- incluye la probabilidad de que existan ambas velocidades que llevan al scattering simultaneamente

- la velocidad relativa multiplicado por la sección eficaz total representa el flujo de partículas hacia el target

Esto ultimo se puede mostrar en forma simple mediante

\Delta v\sigma\sim\displaystyle\frac{dX}{dt}S\sim \displaystyle\frac{dV}{dt}\sim J

ID:(9177, 0)


Simulador camino aleatorio con scattering de Compton
Nota

Se puede estudiar el modelo de Klein-Nishina en forma numérica. Para ello se muestra

- la sección eficaz total en función de la energía del foton
- la sección diferencial en función del angulo para las energías mínima, media y máxima que se definan
- lo que seria la sección eficaz total en un sistema unidimensional que da según la energía transmisión o reflexión

ID:(9114, 0)


Modelamiento con Scattering (2D)
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

El ngulo s lido se define mediante

$d\Omega=2\pi \sin\theta d\theta$

(ID 9147)

El scattering de Compton ocurre cuando un fot n interactua con una part cula cargada, en particular con un electr n. En el proceso el fot n pierde energ a y se desv a poniendo el electr n en movimiento:

(ID 9176)

El largo de onda de Compton se define mediante

$\lambda_c=\displaystyle\frac{h}{m_ec}$

donde h es la constante de Planck, m_e la masa del electr n y c la velocidad de la luz.

(ID 9146)

Los scattering que contribuyen (in) o describen el abandono de part culas (out) se pueden graficar de la siguiente forma:

Gr fica Scattering entre dos part culas

Hay que notar que el termino colisi n:

- integra sobre todas las velocidades externas a las del volumen

- incluye la probabilidad de que existan ambas velocidades que llevan al scattering simultaneamente

- la velocidad relativa multiplicado por la secci n eficaz total representa el flujo de part culas hacia el target

Esto ultimo se puede mostrar en forma simple mediante

\Delta v\sigma\sim\displaystyle\frac{dX}{dt}S\sim \displaystyle\frac{dV}{dt}\sim J

(ID 9177)

El scattering de Compton ocurre cuando un foton interactua con un electr n transfiirendole el primero energ a al segundo (interacci n inel stica). El largo de onda con que emerge del scatering el foton se puede calcular mediante

$\lambda_2=\lambda+\lambda_c(1-\cos\theta)$



en donde

$\lambda_c=\displaystyle\frac{h}{m_ec}$

es el largo de onda de Compton y \theta el angulo de desv o del foton.

(ID 9145)

En el caso de scattering de Compton, la secci n eficaz diferencial es seg n Klein-Nishina

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



donde

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



es la secci n eficaz de Thomson y el factor

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

es la energ a normalizada.

(ID 9144)

Si se toma la secci n eficaz diferencial seg n Klein-Nishina

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



y se integra en el angulo solido

$d\Omega=2\pi \sin\theta d\theta$



se obtiene la secci n eficaz total

$\sigma_{KN}=\displaystyle\frac{3}{4}\sigma_T\left(\displaystyle\frac{(1+\epsilon)}{\epsilon^3}\left(\displaystyle\frac{2\epsilon(1+\epsilon)}{1+2\epsilon}-\log(1+2\epsilon)\right)+\displaystyle\frac{\log(1+2\epsilon)}{2\epsilon}-\displaystyle\frac{(1+3\epsilon)}{(1+2\epsilon)^2}\right)$



donde

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



es la secci n eficaz de Thomson y el factor

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

es la energ a normalizada.

En el limite de peque os \epsilon\ll 1 se tiene que la secci n total es

\sigma_{KN}\sim\sigma_T\left(1-2\epsilon+\displaystyle\frac{26}{5}\epsilon^2\ldots\right)

y en el limite \epsilon\gg 1 se tiene que la secci n total es

\sigma_{KN}\sim\displaystyle\frac{3}{8}\displaystyle\frac{\sigma_T}{\epsilon}\left(\log(2\epsilon)+\displaystyle\frac{1}{2}\right)

(ID 9111)

La secci n eficaz total de Thomson es igual a 2/3 de la superficie de una esfera de radio r_0

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$

El radio r_0 corresponde al radio cl sico del electr n que se define como e^2/m_ec^2.

(ID 9112)

Para simplificar se introduce la energ a inicial del foton E, normalizada por m_ec^2

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

donde m_e es la masa del electr n y c la velocidad de la luz.

(ID 9113)

Se puede estudiar el modelo de Klein-Nishina en forma num rica. Para ello se muestra

- la secci n eficaz total en funci n de la energ a del foton
- la secci n diferencial en funci n del angulo para las energ as m nima, media y m xima que se definan
- lo que seria la secci n eficaz total en un sistema unidimensional que da seg n la energ a transmisi n o reflexi n

(ID 9114)

ID:(1155, 0)