Compton Scattering
Definition 
Compton scattering occurs when a photon interacts with a charged particle, in particular with an electron. In the process the photon loses energy and deviates by putting the electron in motion:

ID:(9176, 0)
Scattering
Image 
Scattering that contributes (in) or describes the abandonment of particles (out) can be plotted as follows:
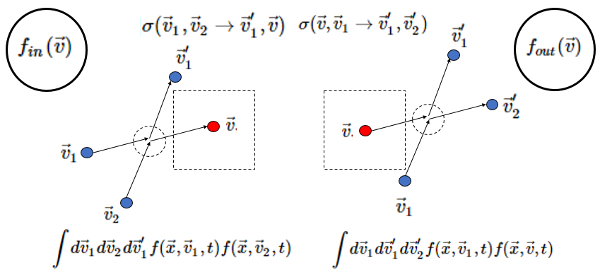
It should be noted that the term collision:
- integrates on all external speeds to those of volume
- includes the likelihood of both speeds leading to scattering simultaneously
- the relative velocity multiplied by the total effective section represents the flow of particles towards the target
The latter can be shown in a simple way through
ID:(9177, 0)
Simulador random walk with Compton scattering
Note 
The Klein-Nishina model can be studied in numerical form. This is shown
- the total effective section as a function of photon energy
- the differential section as a function of the angle for the minimum, medium and maximum energies defined
- what would be the total effective section in a one-dimensional system that gives according to the energy transmission or reflection
ID:(9114, 0)
Modeling with Scattering (2D)
Storyboard 
Variables
Calculations
Calculations
Equations
Examples
Compton scattering occurs when a photon interacts with an electron by transferring the first energy to the second (inelastic interaction). The wavelength of the photon after the scattering can be calculated by
where
Compton wave length and
Compton scattering occurs when a photon interacts with a charged particle, in particular with an electron. In the process the photon loses energy and deviates by putting the electron in motion:
In the case of Compton scattering, the differential effective section is according to Klein-Nishina
where
is the Thomson total effective section and the
is the normalized energy.
The Compton wavelength is defined by
where
Scattering that contributes (in) or describes the abandonment of particles (out) can be plotted as follows:
It should be noted that the term collision:
- integrates on all external speeds to those of volume
- includes the likelihood of both speeds leading to scattering simultaneously
- the relative velocity multiplied by the total effective section represents the flow of particles towards the target
The latter can be shown in a simple way through
The solid angle is defined by
If the differential effective section is taken according to Klein-Nishina
and integrates in the solid angle
the total effective section is obtained
where
is the effective section of Thomson and the
is the normalized energy.
At the limit of small
and in the limit
The total effective section of Thomson is equal to 2/3 of the surface of a sphere of radius
The radius
To simplify we introduce the initial energy of the photon
where
The Klein-Nishina model can be studied in numerical form. This is shown
- the total effective section as a function of photon energy
- the differential section as a function of the angle for the minimum, medium and maximum energies defined
- what would be the total effective section in a one-dimensional system that gives according to the energy transmission or reflection
ID:(1155, 0)
