Benützer:


Anwendung auf die Dosis Berechnung
Storyboard

Da die Boltzmann-Gleichung Kollisionen zwischen Partikeln beinhaltet, ist es möglich, die an das Gewebe abgegebene Energie und damit die Dosis in der Strahlentherapie abzuschätzen. Größere Effizienz wird durch die Bearbeitung von Partikelverteilungen (Photonen, Elektronen und Positronen) anstelle von Einzelpartikeln wie im Fall von Monte Carlo erreicht. Die Einführung von Zellen mit der Lattice Boltzmann Methode (LBM) sollte auch die Möglichkeit ermöglichen, die Präzision nach den bereitgestellten Rechenressourcen zu wählen. Dies bedeutet, dass der Algorithmus in der Lage sein sollte, kontinuierlich von einem System entsprechend Bleistift Beam, Faltung zu Monte Carlo passieren.

>Modell

ID:(1164, 0)


Scattering
Definition

Die Streuung, die die Abgabe von Partikeln (out) beiträgt oder beschreibt, kann wie folgt aufgetragen werden:

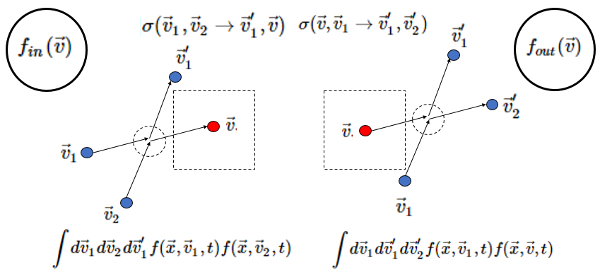
Es ist zu beachten, dass der Begriff Kollision:

- integriert auf alle externen Geschwindigkeiten zu denen des Volumens

- beinhaltet die Wahrscheinlichkeit, dass beide Geschwindigkeiten gleichzeitig zur Streuung führen

- die Relativgeschwindigkeit multipliziert mit dem gesamten effektiven Abschnitt stellt den Strom von Partikeln zum Ziel dar

Letzteres kann auf einfache Weise dargestellt werden

\Delta v\sigma\sim\displaystyle\frac{dX}{dt}S\sim \displaystyle\frac{dV}{dt}\sim J

ID:(9177, 0)


Anwendung auf die Dosis Berechnung
Beschreibung

Da die Boltzmann-Gleichung Kollisionen zwischen Partikeln beinhaltet, ist es möglich, die an das Gewebe abgegebene Energie und damit die Dosis in der Strahlentherapie abzuschätzen. Größere Effizienz wird durch die Bearbeitung von Partikelverteilungen (Photonen, Elektronen und Positronen) anstelle von Einzelpartikeln wie im Fall von Monte Carlo erreicht. Die Einführung von Zellen mit der Lattice Boltzmann Methode (LBM) sollte auch die Möglichkeit ermöglichen, die Präzision nach den bereitgestellten Rechenressourcen zu wählen. Dies bedeutet, dass der Algorithmus in der Lage sein sollte, kontinuierlich von einem System entsprechend Bleistift Beam, Faltung zu Monte Carlo passieren.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$f_{in}$
f_in
Contribución a la función distribución que ingresan (gana)
-
$f_{out}$
f_out
Contribución a la función distribución que salen (pierde)
-
$f$
f
Función distribución de la teoría de transporte
-
$\sigma$
sigma
Sección eficaz de la colisión $(\vec{v}_1,\vec{v}_2\rightarrow\vec{v}'_1,\vec{v}'_2)$
m^2
$t$
t
Tiempo
s
$\tau$
tau
Tiempo de relajamiento
s
$v$
v
Velocidad de la partícula que afecta la distribución
m/s
$v_1$
v_1
Velocidad partícula 1 que colisiona
m/s
$v_21$
v_21
Velocidad partícula 1 que resulta de la colisión
m/s
$v_2$
v_2
Velocidad partícula 2 que colisiona
m/s
$v_22$
v_22
Velocidad partícula 2 que resulta de la colisión
m/s

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Para el caso en que se consideran fotones t rmicos uniformemente distribuidos su n mero por celda ser seg n la distribuci n de Bose-Einstein

$\displaystyle\frac{1}{e^{\hbar\omega/kT}-1}$

donde $\hbar$ es la constante de Planck dividida por $2\pi$, $\omega$ es la velocidad angular, $k$ la constante de Boltzmann y $T$ la temperatura.

Si el flujo es isotr pico se tendr que las $m$ componentes ser n iguales y por ello:

$f_i^{eq}=\displaystyle\frac{1}{e^{\hbar\omega/kT}-1}$

(ID 8561)

Die Streuung, die die Abgabe von Partikeln (out) beitr gt oder beschreibt, kann wie folgt aufgetragen werden:

Es ist zu beachten, dass der Begriff Kollision:

- integriert auf alle externen Geschwindigkeiten zu denen des Volumens

- beinhaltet die Wahrscheinlichkeit, dass beide Geschwindigkeiten gleichzeitig zur Streuung f hren

- die Relativgeschwindigkeit multipliziert mit dem gesamten effektiven Abschnitt stellt den Strom von Partikeln zum Ziel dar

Letzteres kann auf einfache Weise dargestellt werden

\Delta v\sigma\sim\displaystyle\frac{dX}{dt}S\sim \displaystyle\frac{dV}{dt}\sim J

(ID 9177)

Wenn die Teilchen kollidieren, variieren die Verteilungsfunktion nach f(\vec{x},\vec{v},t) so dass\\n\\n

$\displaystyle\frac{df}{dt}\neq 0$



Kollisionen verursachen, dass Teilchen benachbarter Zellen einer Kollision unterliegen, die sie in die betroffene Zelle bringt und Partikel innerhalb der zu vertauschten Zelle. Die erste f hrt zu einer Zunahme von f_{in} Partikeln und der zweite zu einem f_{out} Zeitverlust \tau. So kann die Boltzmann-Transportgleichung mit Kollisionen als geschrieben werden

$\displaystyle\frac{df}{dt}=\displaystyle\frac{1}{\tau}(f_{in}-f_{out})$

(ID 9077)

Die die Zelle verl ssen tragen bei mit

$f(\vec{x},\vec{v}_1,t)f(\vec{x},\vec{v}_2,t)|\vec{v}_2-\vec{v}_1|\sigma(\vec{v}_1,\vec{v}_2\rightarrow\vec{v}_12,\vec{v}_22)d\vec{v}_12d\vec{v}_22$



Integration ber eine der Ausgangsgeschwindigkeiten und beide resultierende Kollision da der andere der Beitrag zur lokalen Verteilungsfunktion ist

$\displaystyle\frac{1}{\tau}f_{out}(\vec{v})=\displaystyle\int d\vec{v}_1d\vec{v}_12d\vec{v}_22f(\vec{x},\vec{v}_1,t)f(\vec{x},\vec{v},t)|\vec{v}-\vec{v}_1|\sigma(\vec{v},\vec{v}_1\rightarrow\vec{v}_12,\vec{v}_22)$

(ID 9080)

Im Fall von Beitr gen zur Zelle m ssen die Beitr ge

$f(\vec{x},\vec{v}_1,t)f(\vec{x},\vec{v}_2,t)|\vec{v}_2-\vec{v}_1|\sigma(\vec{v}_1,\vec{v}_2\rightarrow\vec{v}_12,\vec{v}_22)d\vec{v}_12d\vec{v}_22$



ber cksichtigung werden. Integrierd man ber die Startgeschwindigkeiten und die bei der Kollision entstehende, da diese zur lokalen Verteilungsfunktion beitragen

$\displaystyle\frac{1}{\tau}f_{in}(\vec{v})=\displaystyle\int d\vec{v}_1d\vec{v}_2d\vec{v}_12f(\vec{x},\vec{v}_1,t)f(\vec{x},\vec{v}_2,t)|\vec{v}_2-\vec{v}_1|\sigma(\vec{v}_1,\vec{v}_2\rightarrow\vec{v}_12,\vec{v})$

(ID 9079)

ID:(1164, 0)