Druyd:Knowledge

Poisson-Verteilungen

Storyboard

In dem Fall, in dem die Wahrscheinlichkeit sehr gering ist, wird die Binomialverteilung auf eine Poisson-Verteilung reduziert.

>Modell

ID:(1555, 0)

Beispielvergleich mit der Poisson-Verteilung

Definition

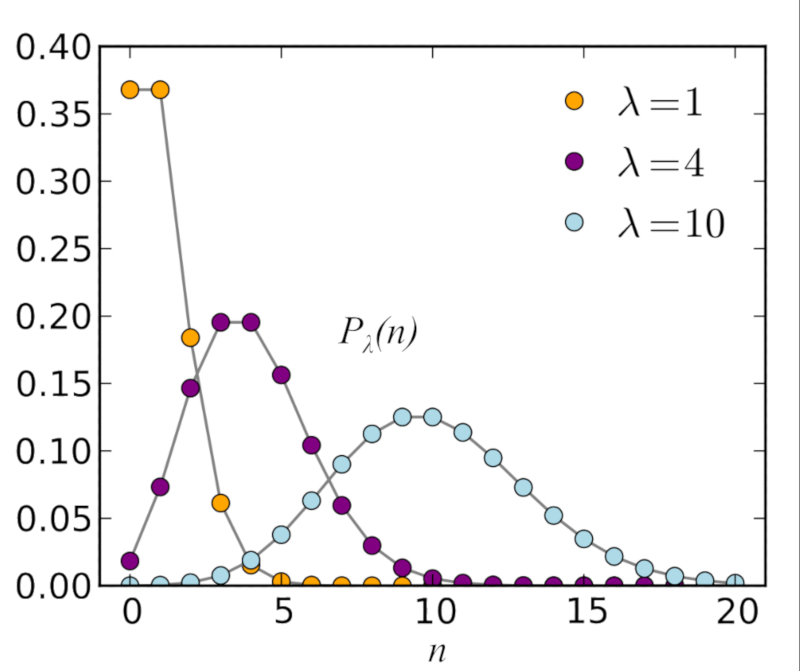
Wenn wir die Binomialverteilung für große Zahlen N und eine sehr kleine Wahrscheinlichkeit p \ ll 1 untersuchen, kann sie mit einer Poisson-Verteilung angenähert werden. Der Vergleich kann mit folgendem Simulator durchgeführt werden:

ID:(7794, 0)

Poisson-Verteilungen

Storyboard

In dem Fall, in dem die Wahrscheinlichkeit sehr gering ist, wird die Binomialverteilung auf eine Poisson-Verteilung reduziert.

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$e^{-\lambda}$

elam

Exponential $e^{-\lambda}$

$N^n$

N^n

Exponential $N^n$

$n!$

Factorial $n!$

$N$

Número total de pasos

$n$

Número totales de pasos a la izquierda

$\lambda^n$

lambda_n

Power of lambda $\lambda^n$

$P_N(m)$

P_Nm

Probabilidad de $n_1$ de $N$ pasos hacia la izquierda

$p$

Probabilidad de pasos hacia la izquierda

$\lambda$

lam

Standard Deviation Poisson

$n$

Zahl

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$ P_{\lambda}(n) =\displaystyle\frac{ \lambda ^ n }{ n! }e^{- \lambda }$

P_lambda(n) =( lambda ^ n / n! )*exp(- lambda )

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$

N^n\sim\displaystyle\frac{N!}{(N-n)!}

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

$\lambda=Np$

lambda=Np

$e^{-\lambda}\sim (1-p)^{N-n}$

e^{-\lambda}\sim (1-p)^{N-n}

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$

\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n

Beispiele

Distribuci n binomial

Con list=8970 la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

equation=8970

con list=3358 el n mero total de pasos es

equation=3358

y solo existe la probabilidad de ir a la derecha o a la izquierda, con list=8965 se tiene para las probabilidades que

equation=8965

por lo que con list se tiene la distribuci n binomial

equation

Anwendung des Sterling-Ansatzes

Daher sind Ausdr cke wie N!/(Nn)! f r N gro (N\gg 1) und n klein (N\gg n) kann mit angen hert werden

equation=8966

mit dem, was Sie mit N\gg n erhalten

\displaystyle\frac{N!}{(N-n)!}\sim\displaystyle\frac{\sqrt{2\pi N}}{\sqrt{2\pi (N-n)}}\displaystyle\frac{N^N}{(N-n)^{N-n}}\displaystyle\frac{e^{N-n}}{e^N}\sim N^n

folglich

equation

Desviaci n Estandard Poison

Sch tzen von $N! p^n/(N-n)! $ wenn $p\sim 0$ und $N\gg n$

Mit der Ann herung

equation=4738

und besch ftigen

equation=8964

es kann gezeigt werden, dass

equation

Sch tzung von $(1-p)^{N-n}$, wenn $p \sim 0$ und $N\gg n$

Wie das Exponential definiert ist als

equation=8967

und durch Eingabe

equation=8964

Sie k nnen z=-\lambda=-Np und u=N-n durch N\gg n welche Ergebnisse ersetzen

equation

Wahrscheinlichkeit f r gro e $N$ und kleine $p$

Da die Wahrscheinlichkeit, n Schritte in eine Richtung zu unternehmen, ist

equation=8961

f r eine gro e Anzahl N und die Wahrscheinlichkeit ist sehr klein p \ll 1 kann angen hert werden

equation=8969

und

equation=8968

Die Binomialverteilung wird auf eine Poisson-Verteilung reduziert:

equation

Beispielvergleich mit der Poisson-Verteilung

Wenn wir die Binomialverteilung f r gro e Zahlen N und eine sehr kleine Wahrscheinlichkeit p \ ll 1 untersuchen, kann sie mit einer Poisson-Verteilung angen hert werden. Der Vergleich kann mit folgendem Simulator durchgef hrt werden:

image

>Modell

ID:(1555, 0)