Coeficiente de elevação
Imagem 
O coeficiente de sustentação é uma função do ângulo de ataque e geralmente segue a tendência indicada na figura a seguir:

No caso ilustrado, a inclinação é de aproximadamente 1,5 para cada 15 graus, ou seja, 0,1 1/gra° ou 5,73 1/rad.
ID:(7148, 0)
Variação do coeficiente de sustentação
Nota 
Tanto aviões como aves são capazes de modificar a forma de suas asas. Os aviões fazem isso através dos flaps, enquanto as aves ajustam a posição de suas penas primárias e secundárias. Dessa forma, ambos conseguem obter um alto coeficiente de sustentação em baixas velocidades durante decolagem e pouso, e um coeficiente de sustentação reduzido em altas velocidades.
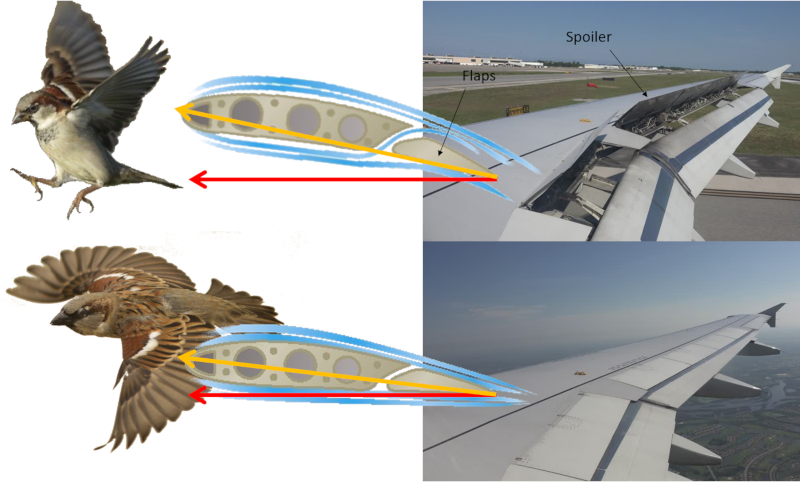
Além disso, os aviões também possuem spoilers que auxiliam na frenagem durante o pouso.
ID:(11072, 0)
Decolagem
Descrição 
A chave para decolar é modificar a asa de modo a obter sustentação suficiente em velocidades mais baixas, permitindo uma decolagem bem-sucedida em um comprimento de pista dado.
Variáveis
Cálculos
Cálculos
Equações
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
e para o coeficiente de elevação ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
(ID 4441)
La força de elevação ($F_L$) junto com la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) representado por
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
o qual, juntamente com la massa corporal ($m$) e la aceleração gravitacional ($g$), deve ser igual a:
| $ F_g = m g $ |
ou seja:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
o que resulta em:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4442)
O coeficiente de elevação ($C_L$) calculado com la massa corporal ($m$), la aceleração gravitacional ($g$), la superfície que gera sustentação ($S_w$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Portanto, com la constante de proporcionalidade do coeficiente de sustentação ($c$) e o aceleração máxima ($\alpha$),
| $ C_L = c \alpha $ |
obtemos
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4443)
Se igualarmos la força de propulsão ($F_p$) com la força de resistência ($F_W$) com o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) em
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
obtemos, para uma la velocidade máxima ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
o que, quando resolvido para a velocidade m xima, resulta em
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
(ID 14507)
La velocidade em relação ao meio ($v$) para um avi o que decola satisfaz a equa o com la aceleração máxima ($a_p$), la velocidade máxima ($v_p$) e o hora de decolagem ($t$):
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
Ao integrar, obtemos a seguinte express o:
$\log(v_p + v) - \log(v_p - v) - \log(v_p + v_0) + \log(v_p - v_0)= \displaystyle\frac{2 a_p}{v_p} t$
Se la velocidade em relação ao meio ($v$) for muito menor do que la velocidade máxima ($v_p$), os logaritmos podem ser expandidos em uma s rie de Taylor, resultando em uma aproxima o de primeira ordem:
| $ v = v_0 + a_p t $ |
(ID 14508)
Uma vez que a velocidade em fun o do tempo dada por
| $ v = v_0 + a_p t $ |
podemos expressar a velocidade como a taxa de varia o da dist ncia em rela o ao tempo:
$\displaystyle\frac{ds}{dt} = \sqrt{2 a_p v_p t }$
Esta equa o pode ser integrada, resultando na rela o entre a dist ncia percorrida e o tempo:
| $ l = v_0 t + \displaystyle\frac{1}{2} a_p t ^2$ |
(ID 14509)
(ID 14515)
Exemplos
(ID 15173)
O coeficiente de sustenta o uma fun o do ngulo de ataque e geralmente segue a tend ncia indicada na figura a seguir:

No caso ilustrado, a inclina o de aproximadamente 1,5 para cada 15 graus, ou seja, 0,1 1/gra ou 5,73 1/rad.
(ID 7148)
Tanto avi es como aves s o capazes de modificar a forma de suas asas. Os avi es fazem isso atrav s dos flaps, enquanto as aves ajustam a posi o de suas penas prim rias e secund rias. Dessa forma, ambos conseguem obter um alto coeficiente de sustenta o em baixas velocidades durante decolagem e pouso, e um coeficiente de sustenta o reduzido em altas velocidades.

Al m disso, os avi es tamb m possuem spoilers que auxiliam na frenagem durante o pouso.
(ID 11072)
(ID 15186)
Para que uma nave ou uma ave possam permanecer em voo, la força gravitacional ($F_g$) deve contrariar a for a da gravidade, que definida por la massa corporal ($m$) e la aceleração gravitacional ($g$). Em outras palavras, deve ser:
| $ F_g = m g $ |
Esta uma situa o simplificada que n o leva em considera o que a for a de resist ncia tamb m pode gerar uma for a de sustenta o.
(ID 14515)
Para gerar uma press o maior abaixo do que acima da asa e gerar sustenta o, utiliza-se o princ pio de Bernoulli, corrigindo a falta de conserva o da densidade de energia com um coeficiente de elevação ($C_L$). A press o sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) atrav s da seguinte f rmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
A condi o para atingir o voo cumprida quando la força de elevação ($F_L$) igual ao peso da aeronave ou ave, calculado a partir de la massa corporal ($m$) e la aceleração gravitacional ($g$). Isso alcan ado com valores suficientes de ERROR:6110,0, la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$), sendo este ltimo coeficiente o fator ajust vel. No caso de aeronaves, os pilotos podem modificar o valor de o coeficiente de elevação ($C_L$) usando flaps, cujo valor deve satisfazer:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Os flaps s o ajustados ao variar o ngulo que a asa faz com a dire o do voo, conhecido como ngulo de ataque.
(ID 4442)
A partir de medi es, conclui-se que o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$:
| $ C_L = c \alpha $ |
Ap s um certo ngulo, a curva diminui at chegar a zero. Isso ocorre porque acima desse ngulo cr tico, os redemoinhos cobrem completamente a superf cie superior da asa, levando perda de sustenta o. Esse fen meno conhecido como \"stall\" (estol em portugu s).
(ID 4441)
Como o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$, podemos calcular o ngulo necess rio para alcan ar sustenta o suficiente para uma velocidade $v$ dada:
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
onde $m$ a massa, $g$ a acelera o gravitacional, $\rho$ a densidade do meio, $S_w$ a rea da asa e $c$ a constante de proporcionalidade entre o coeficiente de sustenta o e o ngulo de ataque.
(ID 4443)
Se durante a decolagem um avi o com la número de propulsores ($n$) perder um motor, la força de propulsão ($F_p$) diminuir , o que pode significar que a aeronave n o conseguir decolar, for ando o piloto a abortar a manobra. No entanto, se la velocidade em relação ao meio ($v$) for maior que o novo valor de la velocidade máxima ($v_p$), poss vel continuar a decolagem com seguran a. Por isso, o piloto monitora constantemente os par metros e informa ao piloto em comando quando a chamada la velocidade crítica $V2$ ($V2$), que a velocidade cr tica, for ultrapassada. Esta velocidade calculada da seguinte forma:
| $ V2 = \sqrt{\displaystyle\frac{ n -1}{n}} v_p $ |
(ID 14477)
La velocidade de rotação $Vr$ ($Vr$) atingido quando o avi o pode decolar ao rotacionar para o ngulo de subida necess rio. Em outras palavras, corresponde ao caso em que, com os valores de la massa corporal ($m$), la aceleração gravitacional ($g$), la constante de proporcionalidade do coeficiente de sustentação ($c$), la aceleração gravitacional ($g$), o perfil total do objeto ($S_p$) e o aceleração máxima ($\alpha$):
| $ Vr = \sqrt{\displaystyle\frac{2 m g }{ \rho C_L S_w }}$ |
(ID 14474)
No in cio da decolagem, a resist ncia aerodin mica, que depende da velocidade, m nima. Portanto, la aceleração máxima ($a_p$) determinada unicamente por la força de propulsão ($F_p$) e la massa corporal ($m$):
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
medida que a resist ncia aerodin mica comece a reduzir a for a de propuls o, essa acelera o inicial ser a m xima poss vel.
(ID 14506)
La força de propulsão ($F_p$) contrabalan a la força de resistência ($F_W$) gerando velocidade, o que, por sua vez, aumenta a mesma for a de resist ncia, conforme descrito em o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) em
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Esse processo continua a aumentar a velocidade at o ponto em que a for a de propuls o iguala a for a de resist ncia, representando a velocidade m xima alcan vel.
Ao igualar a for a de propuls o com a for a de resist ncia e resolver para a velocidade, obtemos la velocidade máxima ($v_p$):
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
medida que a resist ncia aerodin mica come a a reduzir a for a de propuls o, essa acelera o inicial ser a m xima poss vel.
(ID 14507)
La velocidade em relação ao meio ($v$) para um avi o que decola satisfaz a equa o com la aceleração máxima ($a_p$), la velocidade máxima ($v_p$) e o hora de decolagem ($t$):
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
Quando integrada no limite ERROR:6110,0, muito menor que ERROR:10075,0, obtemos:
| $ v = v_0 + a_p t $ |
Normalmente, a velocidade de decolagem de uma aeronave significativamente menor do que a velocidade m xima la velocidade máxima ($v_p$). Portanto, a equa o pode ser resolvida de forma anal tica, como explicado no desenvolvimento.
(ID 14508)
Dado que a velocidade de decolagem, representada como $v$, varia em fun o do tempo $t$ de acordo com a equa o
| $ v = v_0 + a_p t $ |
podemos calcular a dist ncia percorrida ao longo da pista integrando essa equa o em rela o ao tempo:
| $ l = v_0 t + \displaystyle\frac{1}{2} a_p t ^2$ |
Por outro lado, ao considerar a velocidade necess ria para a decolagem, podemos determinar o tempo necess rio para atingi-la e, utilizando a dist ncia percorrida, calcular o comprimento da pista necess rio para a decolagem.
(ID 14509)
ID:(1464, 0)
