Efeito de estol
Storyboard 
Se o ângulo de ataque for muito grande, os vórtices que se formam na parte superior traseira da asa tendem a avançar até atingir a borda superior na parte frontal da asa, cobrindo toda a parte superior com vórtices. Nessa condição, a sustentação diminui drasticamente, o que gera o que é chamado de efeito de estol (stall) e pode levar a uma queda descontrolada do objeto (avião/ave).
Existem situações em que tanto aviões quanto aves usaram esse efeito para realizar ataques surpresa a partir de grande altitude, desenvolvendo uma técnica para recuperar o controle do voo e evitar colisões com o solo.
ID:(1462, 0)
Coeficiente de elevação
Imagem 
O coeficiente de sustentação é uma função do ângulo de ataque e geralmente segue a tendência indicada na figura a seguir:

No caso ilustrado, a inclinação é de aproximadamente 1,5 para cada 15 graus, ou seja, 0,1 1/gra° ou 5,73 1/rad.
ID:(7148, 0)
Asa no fluxo
Nota 
Em um modelo de asa em um túnel de vento, pode-se observar como o fluxo inicialmente é laminar, mas à medida que avança em direção à extremidade traseira da asa, o fluxo se torna turbulento:
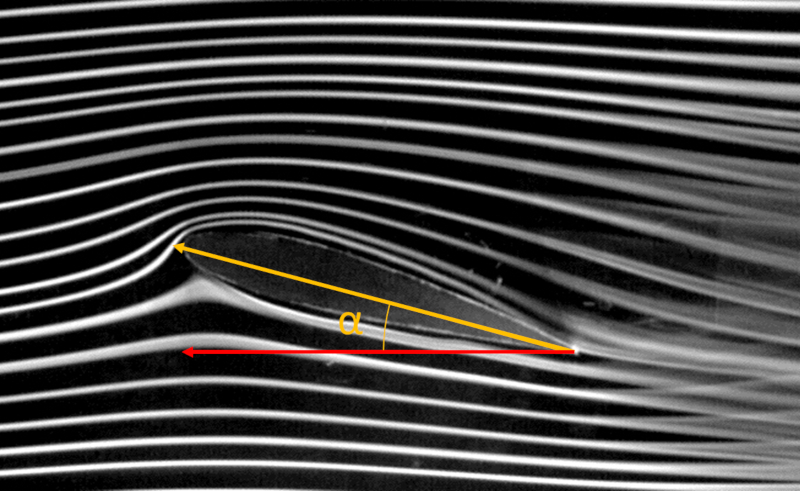
Quando o ângulo de ataque ultrapassa um ângulo crítico (geralmente entre 15 e 30 graus, dependendo do projeto), a superfície da asa fica coberta por vórtices e a sustentação cai abruptamente para zero.

Nesse ponto, ocorre um fenômeno conhecido como estol (stall), em que o fluxo de ar sobre a asa se separa e formam-se vórtices turbulentos. Esses vórtices interrompem o fluxo suave de ar, reduzindo significativamente a sustentação e afetando a capacidade de controle da aeronave. É fundamental evitar que o ângulo de ataque ultrapasse esse valor crítico para manter o voo estável e seguro.
ID:(1165, 0)
Caso de estol
Citar 
Se o ângulo de ataque exceder um ângulo crítico (geralmente entre 15 e 30 graus, dependendo do projeto), a superfície da asa acaba sendo coberta por vórtices e a sustentação cai abruptamente para zero.
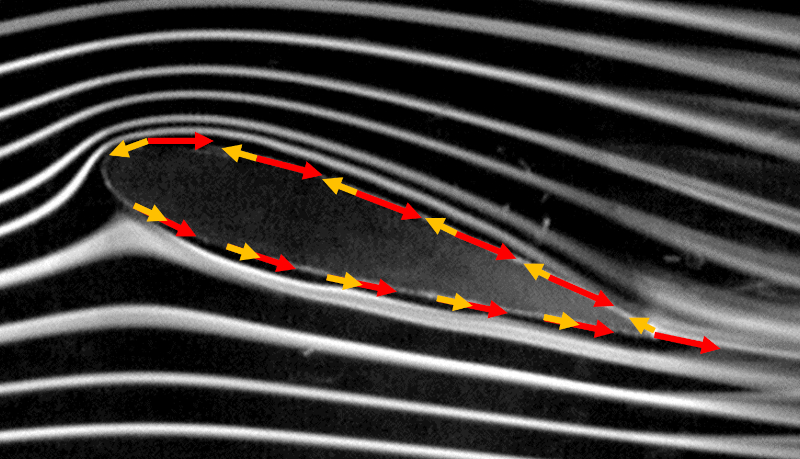
Nesse ponto, ocorre um fenômeno conhecido como entrada em perda (stall), em que o fluxo de ar sobre a asa se separa e vórtices turbulentos são gerados. Esses vórtices interrompem o fluxo suave do ar, reduzindo drasticamente a sustentação e afetando a capacidade de controle da aeronave. É importante evitar que o ângulo de ataque ultrapasse esse ângulo crítico para manter o voo estável e seguro.
ID:(1164, 0)
Case em Boeing 747 Cargo Bagram, Afeganistão
Exercício 
O voo da National Airlines 102, uma aeronave de carga Boeing 747-400 que decolava de Bagram, no Afeganistão, sofreu um trágico acidente em 29 de abril de 2013, devido ao deslocamento de carga durante a decolagem. O deslocamento da carga causou um aumento no ângulo de ataque, levando à perda de sustentação da asa, um fenômeno conhecido como estol. Além disso, o deslocamento da carga danificou o sistema hidráulico dos lemes de cauda, tornando a aeronave incontrolável. Infelizmente, os 7 membros da tripulação perderam a vida instantaneamente no impacto.
Aqui está uma simulação que mostra a trágica decolagem: Simulação
ID:(11066, 0)
Efeito de estol
Descrição 
Se o ângulo de ataque for muito grande, os vórtices que se formam na parte superior traseira da asa tendem a avançar até atingir a borda superior na parte frontal da asa, cobrindo toda a parte superior com vórtices. Nessa condição, a sustentação diminui drasticamente, o que gera o que é chamado de efeito de estol (stall) e pode levar a uma queda descontrolada do objeto (avião/ave). Existem situações em que tanto aviões quanto aves usaram esse efeito para realizar ataques surpresa a partir de grande altitude, desenvolvendo uma técnica para recuperar o controle do voo e evitar colisões com o solo.
Variáveis
Cálculos
Cálculos
Equações
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
e para o coeficiente de elevação ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
(ID 4441)
La força de elevação ($F_L$) junto com la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) representado por
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
o qual, juntamente com la massa corporal ($m$) e la aceleração gravitacional ($g$), deve ser igual a:
| $ F_g = m g $ |
ou seja:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
o que resulta em:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4442)
O coeficiente de elevação ($C_L$) calculado com la massa corporal ($m$), la aceleração gravitacional ($g$), la superfície que gera sustentação ($S_w$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Portanto, com la constante de proporcionalidade do coeficiente de sustentação ($c$) e o aceleração máxima ($\alpha$),
| $ C_L = c \alpha $ |
obtemos
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
(ID 4443)
Exemplos
(ID 15176)
O coeficiente de sustenta o uma fun o do ngulo de ataque e geralmente segue a tend ncia indicada na figura a seguir:

No caso ilustrado, a inclina o de aproximadamente 1,5 para cada 15 graus, ou seja, 0,1 1/gra ou 5,73 1/rad.
(ID 7148)
Em um modelo de asa em um t nel de vento, pode-se observar como o fluxo inicialmente laminar, mas medida que avan a em dire o extremidade traseira da asa, o fluxo se torna turbulento:

Quando o ngulo de ataque ultrapassa um ngulo cr tico (geralmente entre 15 e 30 graus, dependendo do projeto), a superf cie da asa fica coberta por v rtices e a sustenta o cai abruptamente para zero.

Nesse ponto, ocorre um fen meno conhecido como estol (stall), em que o fluxo de ar sobre a asa se separa e formam-se v rtices turbulentos. Esses v rtices interrompem o fluxo suave de ar, reduzindo significativamente a sustenta o e afetando a capacidade de controle da aeronave. fundamental evitar que o ngulo de ataque ultrapasse esse valor cr tico para manter o voo est vel e seguro.
(ID 1165)
Se o ngulo de ataque exceder um ngulo cr tico (geralmente entre 15 e 30 graus, dependendo do projeto), a superf cie da asa acaba sendo coberta por v rtices e a sustenta o cai abruptamente para zero.

Nesse ponto, ocorre um fen meno conhecido como entrada em perda (stall), em que o fluxo de ar sobre a asa se separa e v rtices turbulentos s o gerados. Esses v rtices interrompem o fluxo suave do ar, reduzindo drasticamente a sustenta o e afetando a capacidade de controle da aeronave. importante evitar que o ngulo de ataque ultrapasse esse ngulo cr tico para manter o voo est vel e seguro.
(ID 1164)
O voo da National Airlines 102, uma aeronave de carga Boeing 747-400 que decolava de Bagram, no Afeganist o, sofreu um tr gico acidente em 29 de abril de 2013, devido ao deslocamento de carga durante a decolagem. O deslocamento da carga causou um aumento no ngulo de ataque, levando perda de sustenta o da asa, um fen meno conhecido como estol. Al m disso, o deslocamento da carga danificou o sistema hidr ulico dos lemes de cauda, tornando a aeronave incontrol vel. Infelizmente, os 7 membros da tripula o perderam a vida instantaneamente no impacto.
Aqui est uma simula o que mostra a tr gica decolagem: Simula o
(ID 11066)
(ID 15189)
Para gerar uma press o maior abaixo do que acima da asa e gerar sustenta o, utiliza-se o princ pio de Bernoulli, corrigindo a falta de conserva o da densidade de energia com um coeficiente de elevação ($C_L$). A press o sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) atrav s da seguinte f rmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
A partir de medi es, conclui-se que o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$:
| $ C_L = c \alpha $ |
Ap s um certo ngulo, a curva diminui at chegar a zero. Isso ocorre porque acima desse ngulo cr tico, os redemoinhos cobrem completamente a superf cie superior da asa, levando perda de sustenta o. Esse fen meno conhecido como \"stall\" (estol em portugu s).
(ID 4441)
A condi o para atingir o voo cumprida quando la força de elevação ($F_L$) igual ao peso da aeronave ou ave, calculado a partir de la massa corporal ($m$) e la aceleração gravitacional ($g$). Isso alcan ado com valores suficientes de ERROR:6110,0, la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$), sendo este ltimo coeficiente o fator ajust vel. No caso de aeronaves, os pilotos podem modificar o valor de o coeficiente de elevação ($C_L$) usando flaps, cujo valor deve satisfazer:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Os flaps s o ajustados ao variar o ngulo que a asa faz com a dire o do voo, conhecido como ngulo de ataque.
(ID 4442)
Como o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$, podemos calcular o ngulo necess rio para alcan ar sustenta o suficiente para uma velocidade $v$ dada:
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
onde $m$ a massa, $g$ a acelera o gravitacional, $\rho$ a densidade do meio, $S_w$ a rea da asa e $c$ a constante de proporcionalidade entre o coeficiente de sustenta o e o ngulo de ataque.
(ID 4443)
ID:(1462, 0)
