Le Cycle Diesel
Description 
Variables
Calculs
Calculs
Équations
En suivant une analogie avec le ERROR:5219,0 pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
| $ c =\displaystyle\frac{ C }{ M }$ |
il existe galement un chaleur spécifique des gaz à volume constant ($c_V$) pour le chauffage volume constant avec a capacité thermique à volume constant ($C_V$) :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
Lors du retrait de le chaleur absorbée ($Q_C$), la temp rature du gaz augmente de $T_1$ $T_4$ dans un processus isobare ( pression constante). Cela implique que nous pouvons utiliser la relation pour ERROR:8085 avec a capacité thermique à volume constant ($C_V$) et ERROR:7510, qui est exprim e par l' quation :
| $ dU = C_V \Delta T $ |
Cela nous am ne aux valeurs de a température à l'état 1 ($T_1$) et a température à l'état 4 ($T_4$) en utilisant la formule :
| $ Q_C = C_V ( T_4 - T_1 )$ |
(ID 11145)
En fournissant le chaleur fournie ($Q_H$), la temp rature du gaz augmente de $T_2$ $T_3$ dans un processus isochore ( volume constant). Cela signifie que nous pouvons utiliser la relation pour ERROR:8085 avec a capacité thermique à volume constant ($C_V$) et ERROR:7510, exprim e par l' quation suivante :
| $ dU = C_V \Delta T $ |
Cela donne les valeurs de a température à l'état 2 ($T_2$) et a température à l'état 3 ($T_3$) comme suit :
| $ Q_H = C_V ( T_3 - T_2 )$ |
(ID 11157)
Lors d'une expansion adiabatique, le gaz respecte la relation impliquant le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Dans ce cas, du point initial 3 au point 4. Cela signifie que pendant l'expansion adiabatique, l' tat du gaz change de le volume compressé ($V_2$) et a température à l'état 3 ($T_3$) Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$) selon :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
(ID 11159)
tant donn qu'en expansion adiabatique, le gaz satisfait la relation avec le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Dans ce cas, du point initial 1 au point 2. Cela signifie que pendant la compression adiabatique, l' tat du gaz passe de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$) comme suit :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
(ID 11160)
Le chaleur absorbée ($Q_C$) est li a capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) selon l' quation suivante :
| $ Q_C = C_V ( T_4 - T_1 )$ |
Et le chaleur fournie ($Q_H$) est li a capacité thermique à volume constant ($C_V$), a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) gr ce l' quation suivante :
| $ Q_H = C_V ( T_3 - T_2 )$ |
Par cons quent, dans l' quation pour a efficacité ($\eta$) repr sent e par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous avons la relation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
(ID 11161)
L'expansion adiabatique est d crite l'aide des variables le indice adiabatique ($\kappa$), a température à l'état 4 ($T_4$), a température à l'état 3 ($T_3$), le volume étendu ($V_1$) et le volume compressé ($V_2$) travers la relation
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Tandis que la compression adiabatique est repr sent e par a température à l'état 1 ($T_1$) et a température à l'état 2 ($T_2$) travers la relation
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
En soustrayant la deuxi me quation de la premi re, nous obtenons
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit la relation
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Et cela nous permet de d finir le facteur de compressibilité Otto ($r$) de la mani re suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
(ID 11162)
A efficacité ($\eta$), en fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$), est calcul l'aide de l' quation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Dans le cas de l'expansion adiabatique, elle est d crite l'aide de le indice adiabatique ($\kappa$), le volume étendu ($V_1$) et le volume compressé ($V_2$) avec la relation suivante :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Et la compression adiabatique est repr sent e par la relation suivante :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Si nous soustrayons la deuxi me quation de la premi re, nous obtenons :
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit la relation :
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Cela nous conduit la d finition de le facteur de compressibilité Otto ($r$) avec l' quation suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Avec tous ces composants, l'efficacit d'un processus utilisant le cycle Otto peut tre calcul e comme suit :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
.
(ID 11163)
Exemples
Le cycle d'Otto comprend quatre tapes principales : l'admission, la compression, la d tente (ou combustion) et l' chappement. Lors de la phase d'admission, le moteur aspire un m lange de carburant et d'air tandis que le piston descend. Ce m lange est ensuite comprim lorsque le piston remonte, ce qui augmente la temp rature et la pression du gaz. Au sommet du mouvement de compression, la bougie d'allumage enflamme le m lange comprim , provoquant une combustion rapide connue sous le nom de temps moteur. Cette combustion pousse le piston vers le bas, fournissant de l' nergie au moteur.
Apr s le temps moteur, la soupape d' chappement s'ouvre et le piston remonte pour expulser les gaz br l s de la combustion hors du cylindre, compl tant ainsi le cycle. Le moteur r p te ensuite ce cycle en continu pendant son fonctionnement.
L'efficacit d'un moteur fonctionnant selon le cycle d'Otto d pend du degr de compression et des propri t s du carburant utilis . Des taux de compression plus lev s conduisent g n ralement une meilleure efficacit , mais n cessitent un carburant plus haut indice d'octane pour pr venir le cliquetis du moteur. Le cycle d'Otto se caract rise par sa rapidit avec chaque tape clairement d finie, contribuant de mani re significative l'efficience globale et la puissance d livr e par les moteurs qui l'utilisent.
(ID 15282)
Sadi Carnot a introduit [1] le concept th orique du premier projet de machine capable de g n rer du travail m canique bas sur un gradient de temp rature. Cela est r alis gr ce un processus dans l'espace pression-volume o la chaleur est ajout e et extraite, comme illustr dans l'image :
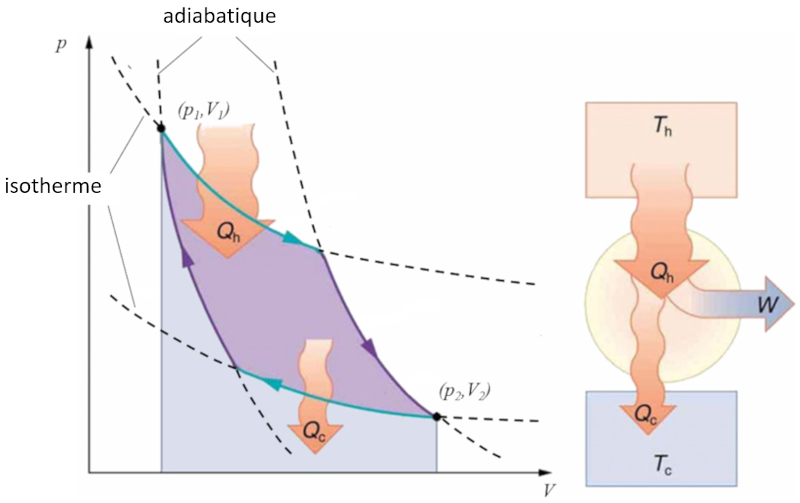
La zone sous la courbe le chaleur fournie ($Q_H$), s' tendant de 1 2, repr sente l' nergie n cessaire pour passer de l' tat ($p_1, V_1$) l' tat ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 1, repr sente l'extraction d' nergie n cessaire pour revenir de l' tat ($p_2, V_2$) l' tat ($p_1, V_1$). La diff rence entre ces zones correspond la r gion d limit e par les deux courbes et repr sente le travail efficace ($W$) que le syst me peut accomplir.
Carnot a galement d montr que, conform ment au deuxi me principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas tre nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
![]() [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance", Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance", Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
(ID 11131)
Le cycle d'Otto [1] peut tre consid r comme une solution technique bas e sur le cycle de Carnot. Dans ce contexte, il se compose de quatre tapes qui se d roulent comme suit :
• tape 1 2 : Compression adiabatique $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• tape 2 3 : Chauffage $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• tape 3 4 : Expansion adiabatique $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• tape 4 1 : Refroidissement $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$
Ces tapes sont illustr es dans le diagramme suivant :
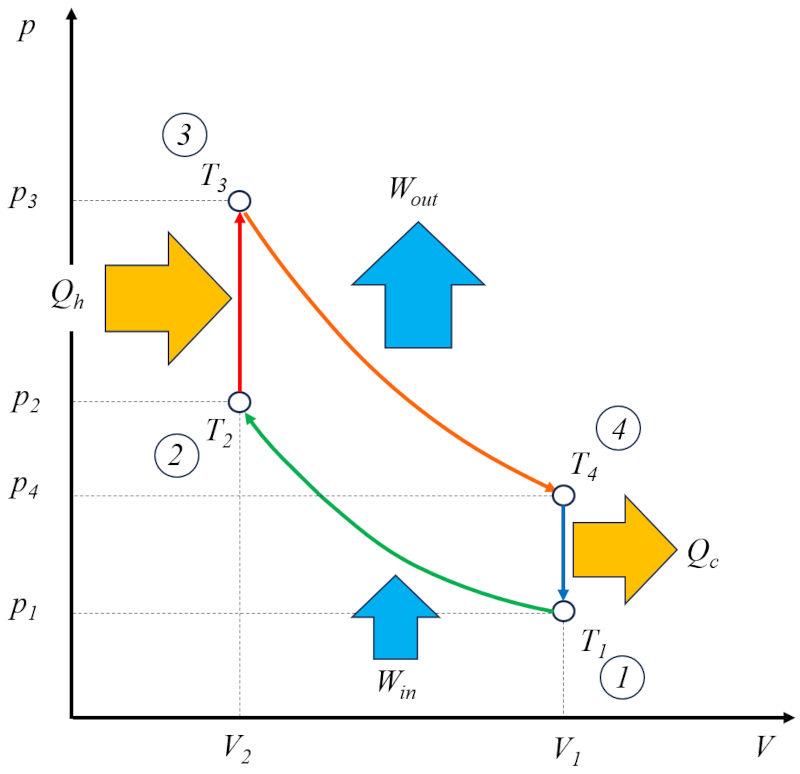
Sur le diagramme, le flux d' nergie est illustr , o le chaleur fournie ($Q_H$) ajoute de l' nergie, faisant monter la temp rature de a température à l'état 2 ($T_2$) A température à l'état 3 ($T_3$). Il entre dans le syst me et effectue un travail efficace ($W$) unit s de travail, tandis que le compl ment le chaleur absorbée ($Q_C$) est absorb , abaissant la temp rature de a température à l'état 4 ($T_4$) A température à l'état 1 ($T_1$).
![]() [1] "Verbrennungsmotor" (Moteur combustion interne), N. A. Otto, Kaiserlichen Patentamts, Brevet 532, 2 janvier 1877.
[1] "Verbrennungsmotor" (Moteur combustion interne), N. A. Otto, Kaiserlichen Patentamts, Brevet 532, 2 janvier 1877.
Note : En 1862, Nikolaus Otto a tent de construire le moteur combustion interne brevet par Alphonse Beau de Rochas sans succ s. Plus tard, il l'a modifi et a r ussi en construire un fonctionnel en 1877, fabriquant 30 000 moteurs silencieux et tr s fiables. Il a brevet son concept en 1877 ; cependant, le brevet a t r voqu ult rieurement en raison de l'existence du brevet d'Alphonse Beau de Rochas, m me si Rochas n'a jamais r ussi construire sa version. Comme Otto a t le premier faire fonctionner le moteur, sa version est aujourd'hui rappel e, d signant le processus comme le "Cycle d'Otto".
(ID 11140)
Le moteur Otto fonctionne selon deux cycles : le cycle Otto proprement dit, qui comprend les phases suivantes :
• Phase 1 2 : Compression adiabatique
• Phase 2 3 : Chauffage
• Phase 3 4 : Expansion adiabatique
• Phase 4 1 : Refroidissement
De plus, il poss de un cycle pour vider les gaz br l s et les remplir d'un nouveau m lange.
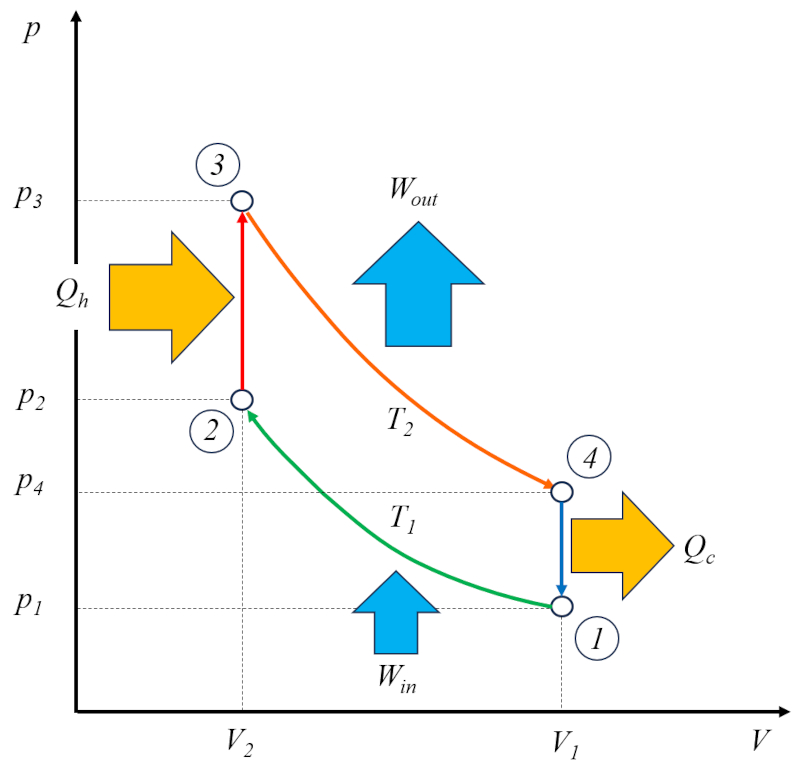
Pour cette raison, il est appel un moteur deux temps. La phase de vidange et de remplissage peut tre r alis e l'aide d'une masse de compensation ou par le biais d'un second cylindre qui fonctionne en d phasage.
L'efficacit a efficacité ($\eta$) du moteur peut tre estim e en utilisant le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) avec l' quation suivante :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
(ID 11142)
Le chaleur absorbée ($Q_C$) est li a capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) selon l' quation suivante :
| $ Q_C = C_V ( T_4 - T_1 )$ |
Et le chaleur fournie ($Q_H$) est li a capacité thermique à volume constant ($C_V$), a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) gr ce l' quation suivante :
| $ Q_H = C_V ( T_3 - T_2 )$ |
Par cons quent, dans l' quation pour a efficacité ($\eta$) repr sent e par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous avons la relation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
(ID 15749)
A efficacité ($\eta$), en fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$), est calcul l'aide de l' quation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Dans le cas de l'expansion adiabatique, elle est d crite l'aide de le indice adiabatique ($\kappa$), le volume étendu ($V_1$) et le volume compressé ($V_2$) avec la relation suivante :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Et la compression adiabatique est repr sent e par la relation suivante :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Si nous soustrayons la deuxi me quation de la premi re, nous obtenons :
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit la relation :
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Cela nous conduit la d finition de le facteur de compressibilité Otto ($r$) avec l' quation suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Avec tous ces composants, l'efficacit d'un processus utilisant le cycle Otto peut tre calcul e comme suit :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
(ID 15750)
(ID 15341)
ID:(1486, 0)
