Viskose-Kraft
Storyboard 
Die viskose Kraft wird in der Regel als proportional zur Geschwindigkeit des Objekts modelliert. Die Konstante der viskosen Kraft ist proportional zur Viskosität des Mediums und zu Faktoren, die mit der Geometrie des Objekts zusammenhängen.
Wenn keine andere Kraft wirkt, tendiert die viskose Kraft dazu, die Bewegung eines Objekts zu verlangsamen, das sich anfangs mit einer bestimmten Geschwindigkeit bewegt.
ID:(1415, 0)
Ostwald-Methode zur Messung der Viskosität
Notiz 
Die Viskositätsmessmethode nach Ostwald basiert auf dem Verhalten eines Flüssigkeitsstroms durch ein Rohr mit kleinem Radius (Kapillare).
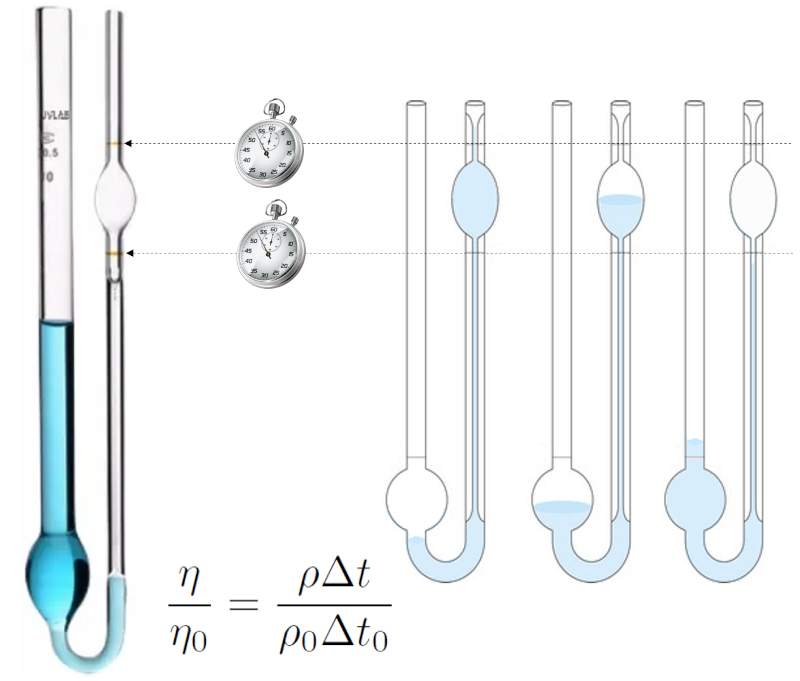
Die Flüssigkeit wird eingeführt, Unterdruck wird angewendet, um die obere Markierung zu überschreiten, und dann wird sie abfließen gelassen, wobei die Zeit gemessen wird, die der Pegel benötigt, um von der oberen zur unteren Markierung zu gelangen.
Das Experiment wird zuerst mit einer Flüssigkeit durchgeführt, deren Viskosität und Dichte bekannt sind (z. B. destilliertes Wasser), und dann mit der Flüssigkeit, für die die Viskosität bestimmt werden soll. Wenn die Bedingungen identisch sind, wird die in beiden Fällen fließende Flüssigkeit ähnlich sein, und somit wird die Zeit proportional zur Dichte durch die Viskosität sein. Somit kann eine Vergleichsgleichung zwischen beiden Viskositäten aufgestellt werden:
ID:(15545, 0)
Viskose-Kraft
Beschreibung 
Die viskose Kraft wird in der Regel als proportional zur Geschwindigkeit des Objekts modelliert. Die Konstante der viskosen Kraft ist proportional zur Viskosität des Mediums und zu Faktoren, die mit der Geometrie des Objekts zusammenhängen. Wenn keine andere Kraft wirkt, tendiert die viskose Kraft dazu, die Bewegung eines Objekts zu verlangsamen, das sich anfangs mit einer bestimmten Geschwindigkeit bewegt.
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 3243)
Da der Moment ($p$) mit die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) definiert ist,
| $ p = m_i v $ |
Wenn die Träge Masse ($m_i$) gleich die Anfangsmasse ($m_0$) ist, k nnen wir den Impuls nach der Zeit ableiten und die Kraft mit konstanter Masse ($F$) erhalten:
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Daher kommen wir zu dem Schluss, dass
| $ F = m_i a $ |
(ID 10975)
Angesichts der Tatsache, dass die Gesamtkraft die Kraft mit konstanter Masse ($F$) gleich minus die Viscose Kraft ($F_v$) ist:
und die Kraft mit konstanter Masse ($F$) aus die Träge Masse ($m_i$) und die Augenblickliche Beschleunigung ($a$) besteht:
| $ F = m_i a $ |
und die Viscose Kraft ($F_v$) aus die Konstante des Viscose Kraft ($b$) und die Geschwindigkeit ($v$) besteht:
| $ F_v = b v $ |
erhalten wir
| $ m_i a = - b v $ |
(ID 14498)
Mit die Geschwindigkeit ($v$), der Zeit ($t$), die Träge Masse ($m_i$) und die Konstante des Viscose Kraft ($b$) haben wir die Gleichung:
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
die mit die Viskositätszeit und träge Masse ($\tau_i$) definiert durch
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
umgeschrieben werden kann als
$\displaystyle\frac{dv}{dt}=-\displaystyle\frac{v}{\tau_i}$
deren L sung ist
| $ v = v_0 e^{- t / \tau_i }$ |
(ID 14500)
(ID 15553)
Beispiele
(ID 15522)
Die Kraft, die ein K rper erf hrt, der sich mit einer Geschwindigkeit von eine Geschwindigkeit ($v$) in einem Medium bewegt, das durch die Konstante des Viscose Kraft ($b$) charakterisiert ist, betr gt die Viscose Kraft ($F_v$), wie durch die Gleichung beschrieben:
| $ F_v = b v $ |
Um die Rolle von die Konstante des Viscose Kraft ($b$) zu verstehen, ist es wichtig, sich daran zu erinnern, dass Viskosit t ein Ma daf r ist, wie sich der Impuls oder die Geschwindigkeit der Molek le ausbreitet. Mit anderen Worten, die Konstante des Viscose Kraft ($b$) ist das Ma daf r, wie viel Energie der K rper verliert, indem er sie an das Medium bertr gt und die Molek le beschleunigt, und ihnen so Energie zuf hrt. Daher ist die Konstante des Viscose Kraft ($b$) proportional zur Viskosit t.
(ID 15546)
Die Viskosit tsmessmethode nach Ostwald basiert auf dem Verhalten eines Fl ssigkeitsstroms durch ein Rohr mit kleinem Radius (Kapillare).
Die Fl ssigkeit wird eingef hrt, Unterdruck wird angewendet, um die obere Markierung zu berschreiten, und dann wird sie abflie en gelassen, wobei die Zeit gemessen wird, die der Pegel ben tigt, um von der oberen zur unteren Markierung zu gelangen.
Das Experiment wird zuerst mit einer Fl ssigkeit durchgef hrt, deren Viskosit t und Dichte bekannt sind (z. B. destilliertes Wasser), und dann mit der Fl ssigkeit, f r die die Viskosit t bestimmt werden soll. Wenn die Bedingungen identisch sind, wird die in beiden F llen flie ende Fl ssigkeit hnlich sein, und somit wird die Zeit proportional zur Dichte durch die Viskosit t sein. Somit kann eine Vergleichsgleichung zwischen beiden Viskosit ten aufgestellt werden:

(ID 15545)
Im Fall eines K rpers, der in einem viskosen Medium f llt, ist die Bewegungsgleichung eine Gleichung von die Geschwindigkeit ($v$) in Abh ngigkeit von der Zeit ($t$) mit die Träge Masse ($m_i$) und die Konstante des Viscose Kraft ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Dies wird erhalten mit die Viskositätszeit und träge Masse ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
Integrieren mit Anfangszeit null und die Anfangsgeschwindigkeit ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
welche nachfolgend dargestellt ist:
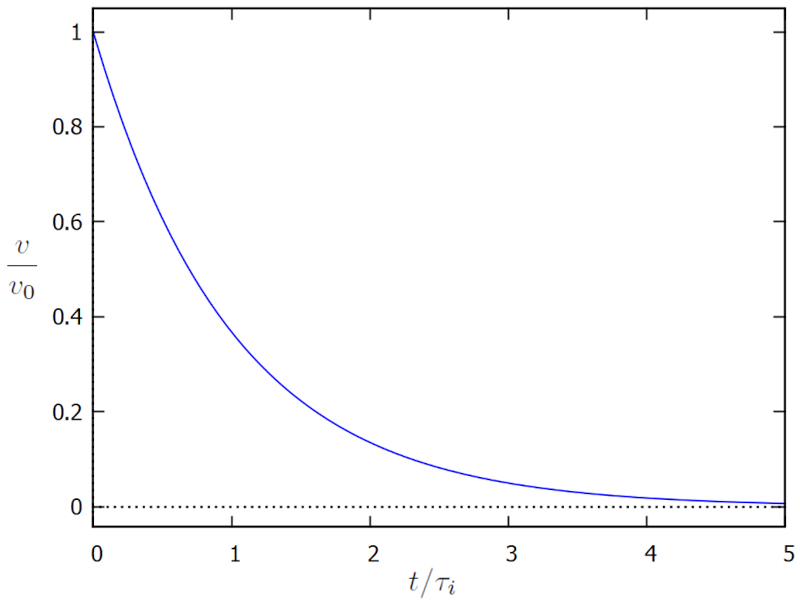
Die Grafik veranschaulicht, wie die Viskosit t den K rper zum Abstieg bis null zwingt, was ungef hr zu einer Zeit von der Gr enordnung von die Viskositätszeit und träge Masse ($\tau_i$) geschieht.
(ID 15552)
Im Fall eines K rpers, der in einem viskosen Medium f llt, ist die Bewegungsgleichung eine Gleichung von die Position ($s$) in Abh ngigkeit von die Anfangsgeschwindigkeit ($v_0$), die Viskositätszeit und träge Masse ($\tau_i$) und der Zeit ($t$):
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
Aus dieser Gleichung erhalten wir durch Integration mit Anfangszeit null und eine Ausgangsstellung ($s_0$):
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
die unten dargestellt ist:
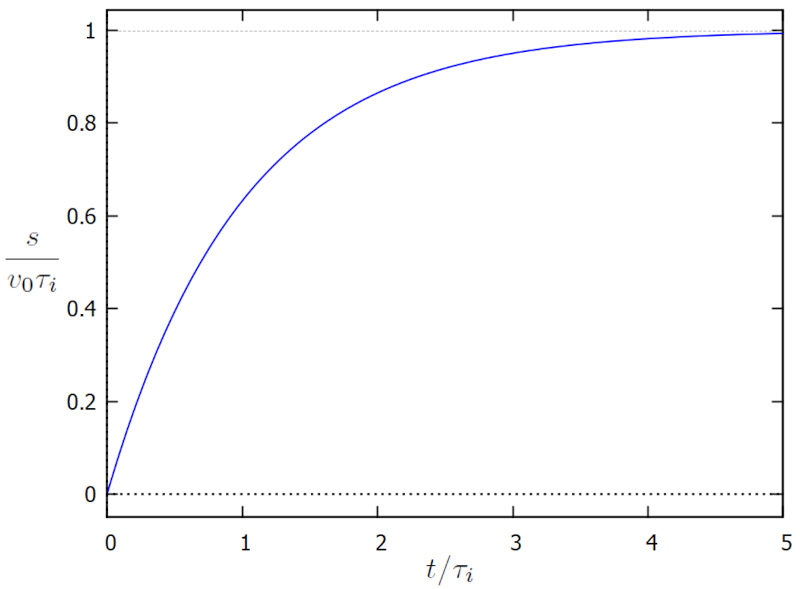
(ID 15551)
(ID 15534)
ID:(1415, 0)
