Stabilité de la flottabilité
Storyboard 
La force générée par la flottaison agit au centre du volume déplacé, qui se trouve généralement plus bas que le centre de masse de l'objet dans l'eau. Cette paire de forces produit des couples qui peuvent stabiliser ou déstabiliser l'objet. Dans le second cas, il peut même se renverser. Ce principe s'applique aussi bien aux objets inanimés qu'aux organismes vivants, qui, en raison de maladies, peuvent avoir du mal à maintenir une position verticale.
ID:(1610, 0)
La catastrophe de Vasa
Image 
Le navire de guerre suédois Vasa est un exemple connu d'un navire instable. Le 10 août 1628, seulement 20 minutes après avoir quitté le chantier naval lors de son voyage inaugural dans le port de Stockholm, le navire a chaviré et a coulé :

La conception du navire était défectueuse, car sa construction étroite visait à atteindre des vitesses élevées et sa structure haute était destinée à accueillir 64 canons, un nombre significatif. Cependant, cette conception rendait le navire intrinsèquement instable, ce qui a entraîné son chavirement avec la première rafale de vent.
Heureusement, le navire a coulé dans des eaux peu profondes et a été conservé dans l\'eau salée pendant 333 ans jusqu\'à sa récupération en 1961. Au début, le navire a été maintenu mouillé, puis lentement remplacé l\'eau par un mélange de cire qui permet de l\'exposer complètement sec dans un musée à quelques mètres de l\'endroit où il a coulé.
Le Vasa sert de rappel dans la construction navale, démontrant l\'importance d\'une conception soigneuse et de la stabilité. Son exposition au musée est une attraction populaire, attirant des visiteurs du monde entier pour voir cette pièce remarquable de l\'histoire maritime.
ID:(11977, 0)
Point d'attaque flottant
Noter 
Le point d'application de la force de poussée est égal au centre de masse du volume de liquide déplacé :
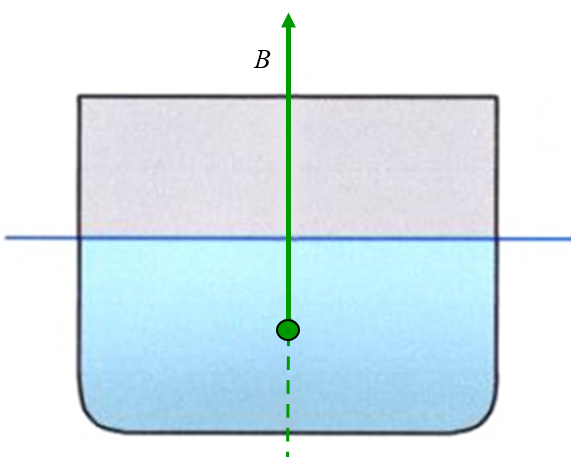
Dans un bateau de profil carré typique, cela correspond à un point situé à mi-profondeur (profondeur d\'immersion).
ID:(11957, 0)
Définir le métacentre
Citation 
Lorsqu'une force latérale est appliquée et que l\'objet est incliné, on peut observer que le point où la force de flottaison agit se déplace hors de l\'axe. En traçant une ligne verticale depuis cette nouvelle position, on obtient que la ligne croise l\'axe central en un point appelé le métacentre :
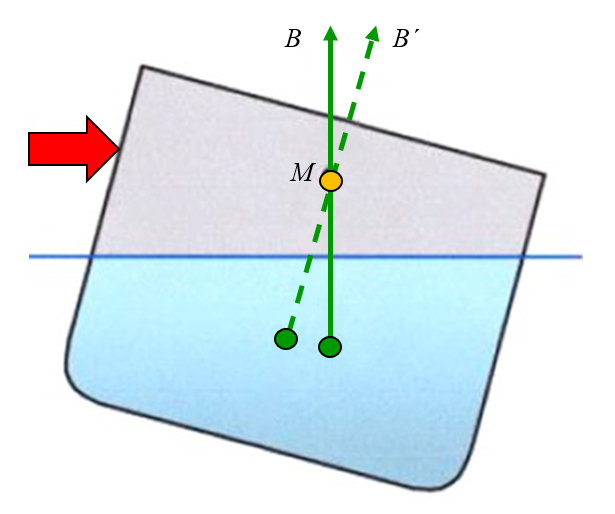
ID:(11959, 0)
Action de la gravité
Exercer 
La gravité agit sur le centre de masse, qui se trouve généralement au-dessus du point d'application de la force de flottabilité, mais peut être au-dessus ou en dessous du métacentre :
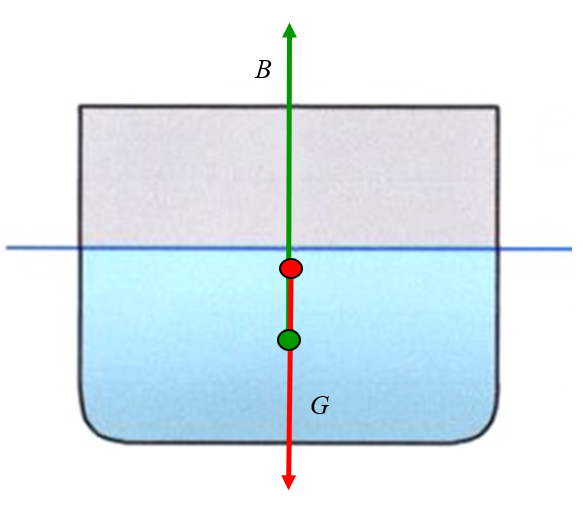
ID:(11960, 0)
Situation stable
Équation 
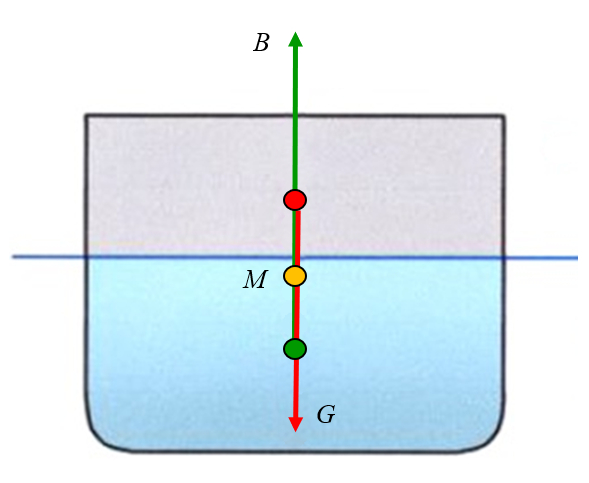
Si le métacentre est situé au-dessus du centre de masse, la force de gravité génère un couple qui a tendance à stabiliser l'objet. C\'est comme si l\'objet était suspendu au métacentre et que la force de gravité génère des rotations autour de celui-ci. Lorsque le centre de masse est situé en dessous du métacentre, le couple génère une rotation vers l\'axe, c\'est-à-dire qu\'il a tendance à corriger l\'inclinaison, stabilisant ainsi l\'objet :
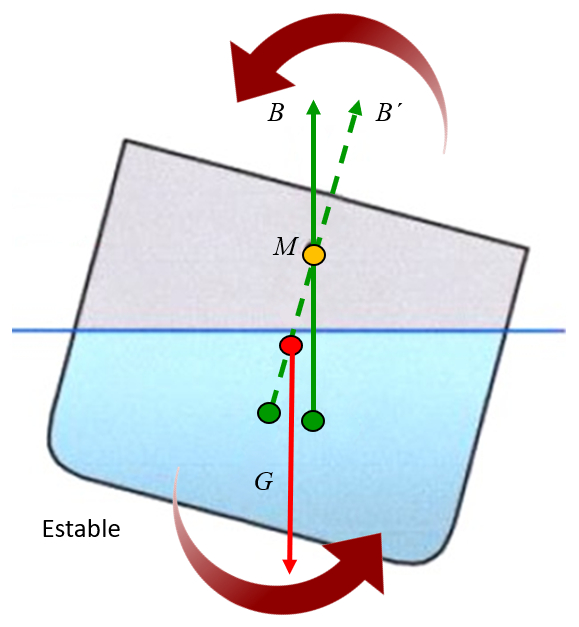
ID:(11961, 0)
Métacentre sous le centre de gravité
Script 
Si le métagcentre peut être situé au-dessus ou en dessous du centre de gravité. Ce dernier peut facilement se produire si une charge est ajoutée sur la partie supérieure, faisant ainsi monter le centre de masse, ce qui rend le système instable.
Note : pour éviter de perdre la stabilité, il est important de positionner la charge dans une position basse (fond du bateau).
ID:(11962, 0)
Situation instable
Variable 
Si le métacentre est situé en dessous du centre de masse, la force de gravité génère un couple qui a tendance à déstabiliser l'objet. C\'est comme si l\'objet était suspendu au métacentre et que la force de gravité génère des rotations autour de celui-ci. Lorsque le centre de masse est situé au-dessus du métacentre, le couple génère une rotation qui l\'éloigne de l\'axe, c\'est-à-dire qu\'il a tendance à augmenter l\'inclinaison et donc à déstabiliser l\'objet :
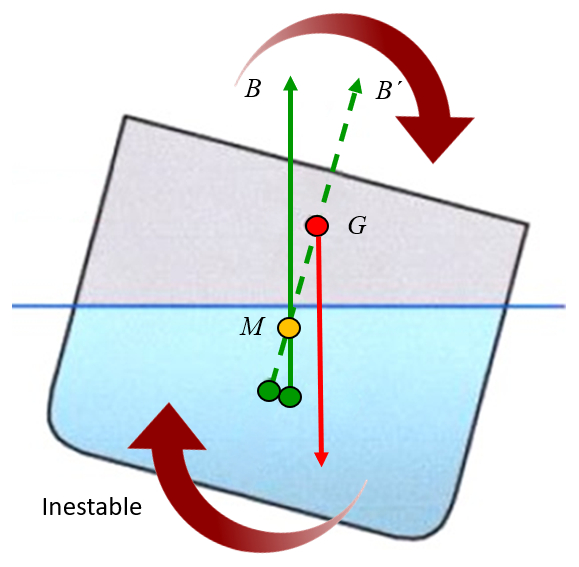
ID:(11963, 0)
Maquette d'une coque de bateau
Audio 
Le modèle de la coque du navire est réduit à un parallélépipède avec des longueurs de le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$), ce qui donne des dimensions de $2a \times 2b \times 2c$, avec un tirant d'eau de un brouillon d'objet ($d$) :
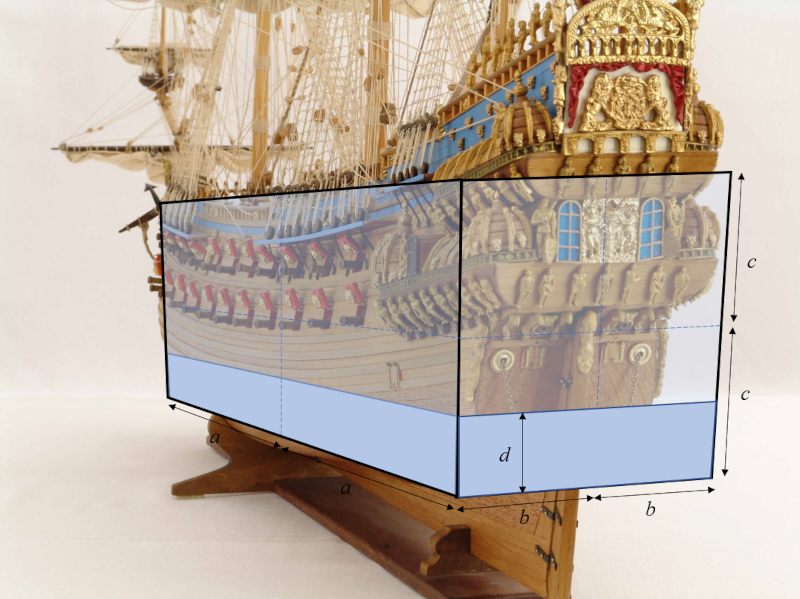
ID:(11969, 0)
Modèle simplifié: parallélépipède rectangle
Video 
Un modèle couramment utilisé pour les bateaux est celui d'un parallélépipède droit avec des longueurs de le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$), et un centre de masse à son centre géométrique. Lorsqu'il est placé dans l'eau, le corps s'enfonce jusqu'à une profondeur de un brouillon d'objet ($d$). La position du centre où la force de flottaison agit peut être vue dans l'image suivante, avec les coordonnées a hauteur du point d'attaque, force de flottabilité ($z_B$), a hauteur du centre de masse ($z_G$) et a hauteur du métacentre ($z_M$) :
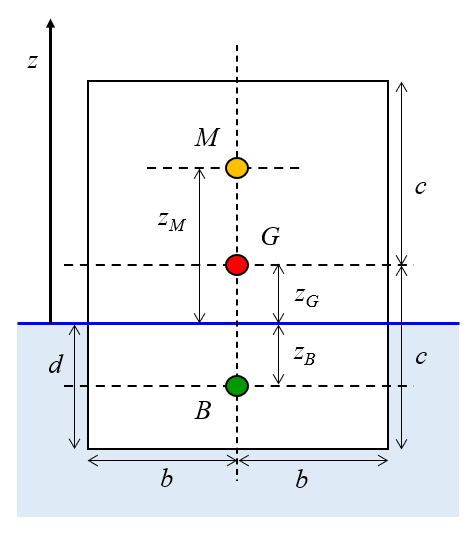
Donc a hauteur du centre de masse ($z_G$) est
| $ z_G = c - d $ |
ID:(11964, 0)
Définir la position du métacentre
Unité 
Le métacentre est calculé en déterminant le centre de masse du corps incliné sous la condition que la surface située sous la ligne de flottaison (ligne bleue) reste constante :
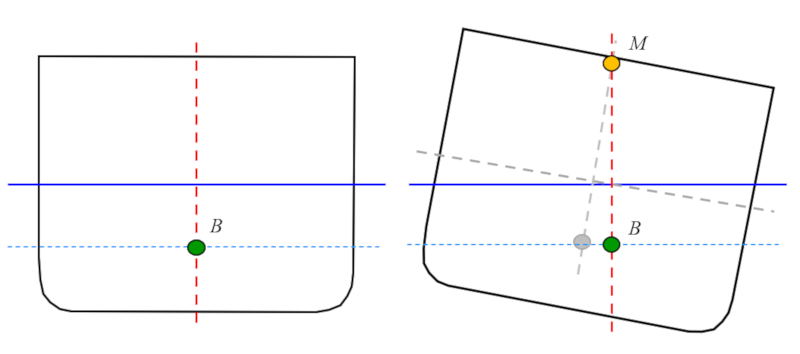
ID:(11979, 0)
Calcul de la position du centre de masse de l'eau déplacée
Code 
Lorsque le bateau gîte, une plus grande section deau se déplace dun côté et la même plus petite section du côté opposé. Le centre de masse est donc déplacé du centre vers le secteur de plus grand déplacement, qui est calculé par
$\bar{x} = \displaystyle\frac{\displaystyle\sum_i m_i x_i}{\displaystyle\sum_i m_i}$
La masse est proportionnelle à la section calculée à partir de le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$) par :
$2b d$
Toutes les masses décalées des deux côtés de l'axe ne contribuent pas au numérateur et seuls les deux triangles indiqués à partir d'une zone avec le angle de gîte ($\phi$)
$b^2\phi$
pondérer la position du centre de masse des triangles
$\displaystyle\frac{2b}{3}$
ce que l'on voit sur le graphique :
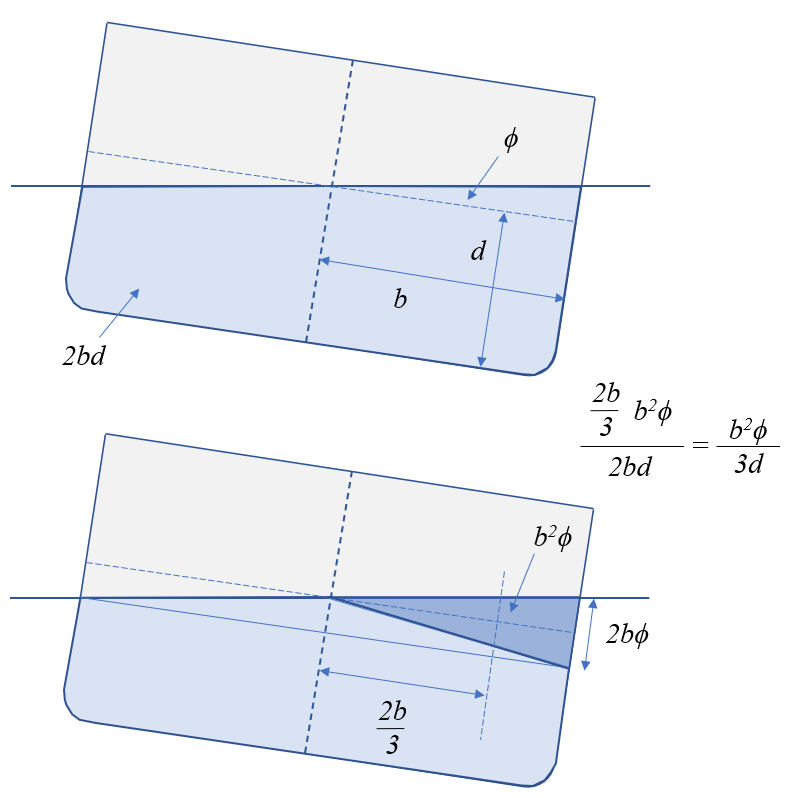
Par conséquent, la distance au centre de masse de leau déplacée par rapport à laxe est
$\displaystyle\frac{\displaystyle\frac{2b}{3} b^2\phi}{2bd}=\displaystyle\frac{b^2\phi}{3d}$
ID:(14248, 0)
Calcul de la position du métacentre
Flux 
Si un navire gîte à Le angle de gîte ($\phi$), le centre de masse de l'eau déplacée se déplace avec le demi-largeur du parallélépipède ($b$) et le demi-longueur du parallélépipède ($a$) sur une distance de :
$\displaystyle\frac{b^2\phi}{3d}$
Puisque cette distance est l'arc de cercle que l'on peut tracer autour du métacentre, la distance entre le métacentre et le centre de masse de l'eau déplacée, qui correspond au rayon, est :
$\displaystyle\frac{b^2}{3d}$
Par conséquent, la position du métacentre doit tenir compte du fait que le centre de coordonnées est à la hauteur de la surface de l'eau, soit une distance $d/2$ au-dessus du centre de masse de l'eau déplacée :
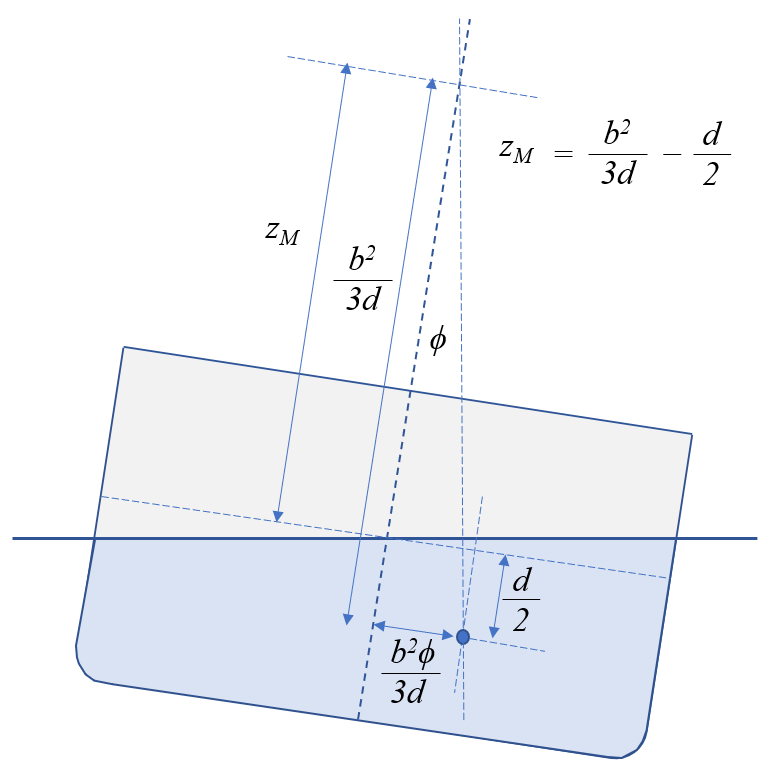
avec a hauteur du métacentre ($z_M$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11967, 0)
Analyse de la condition de stabilité du parallélépipède
Matrice 
Pour que le parallélépipède soit stable, a hauteur du métacentre ($z_M$) doit toujours être supérieur ou égal à A hauteur du centre de masse ($z_G$), c'est-à-dire
| $ z_M \geq z_G $ |
Par conséquent, avec a hauteur du centre de masse ($z_G$) étant le point d'application de la force de flottaison donnée avec a mi-hauteur du parallélépipède ($c$) et le brouillon d'objet ($d$) :
| $ z_G = c - d $ |
et a hauteur du métacentre ($z_M$) étant avec le demi-largeur du parallélépipède ($b$) :
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
nous obtenons a condition de stabilité d'un corps flottant ($e$) :
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
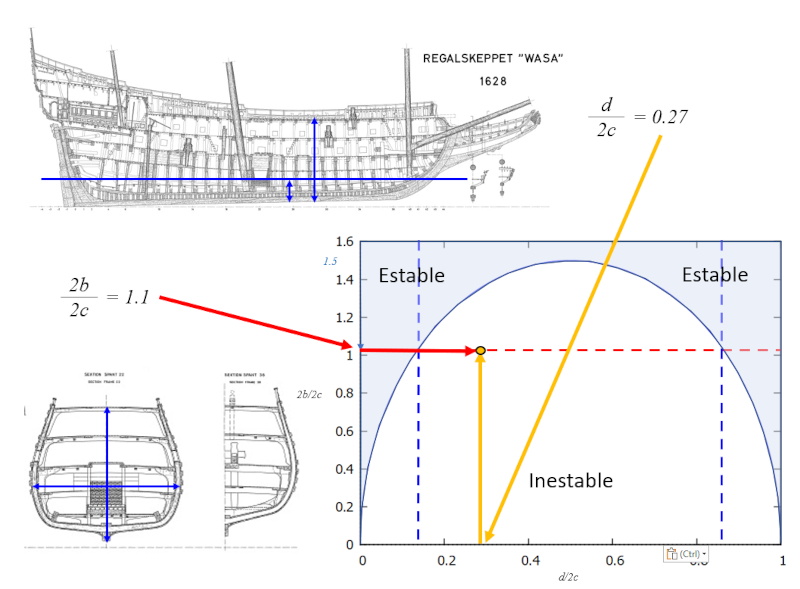
ce qui signifie qu'il y a une région dans le graphe $b/c$ (largeur/profondeur) versus $d/2c$ (profondeur/hauteur) dans laquelle le système est stable, et dans son complément, instable :
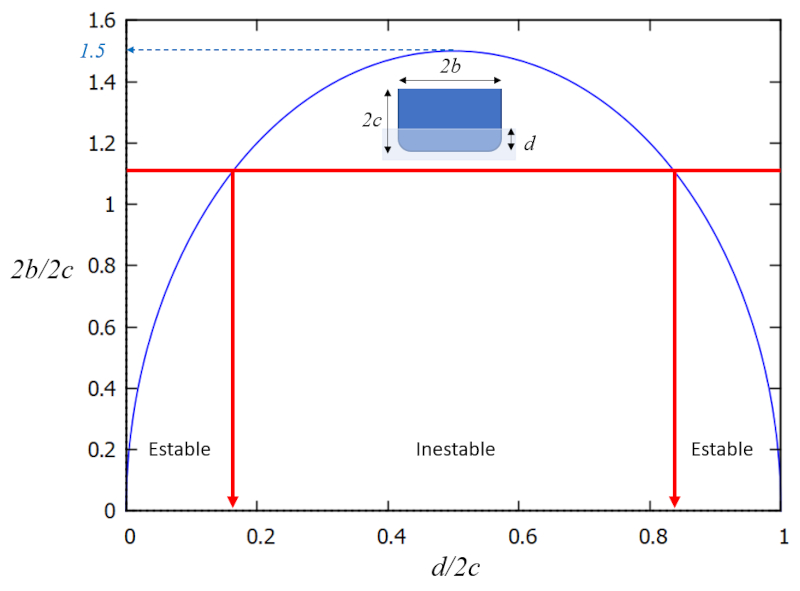
En d'autres termes, la stabilité est obtenue avec des valeurs élevées de $b/c$ (largeur supérieure au tirant d'eau). Dans le cas du navire Vasa, le problème était que le navire était trop haut pour sa largeur. Une solution aurait été de "l'enfoncer plus profondément" ou d'atteindre une valeur $d/c$ plus élevée pour éviter la zone d'instabilité. Cependant, cela n'était pas possible en raison des ouvertures pour les canons par lesquelles l'eau aurait pu entrer.
Pour plus d'informations sur les erreurs de construction, consultez Pourquoi le Vasa a coulé : 10 problèmes et quelques antidotes pour les projets logiciels, Richard E. Fairley, Mary Jane Willshire, mars/avril 2003 IEEE LOGICIEL, qui s'applique aux projets logiciels.
ID:(11976, 0)
Analyse de l\'affaire Wasa
Html 
En étudiant les plans du Vasa, il est possible d\'estimer les coefficients de la relation entre la largeur et la hauteur, ainsi que entre le tirant d\'eau et la hauteur. Cette analyse révèle que le navire est instable:
ID:(14247, 0)
Stabilité de la flottabilité
Description 
La force générée par la flottaison agit au centre du volume déplacé, qui se trouve généralement plus bas que le centre de masse de l'objet dans l'eau. Cette paire de forces produit des couples qui peuvent stabiliser ou déstabiliser l'objet. Dans le second cas, il peut même se renverser. Ce principe s'applique aussi bien aux objets inanimés qu'aux organismes vivants, qui, en raison de maladies, peuvent avoir du mal à maintenir une position verticale.
Variables
Calculs
Calculs
Équations
A force de poussée ($F_b$) est d termin par a densité du liquide ($\rho_w$), le volume déplacé ($V_b$) et a accélération gravitationnelle ($g$) comme :
| $ F_b = \rho_w V_b g $ |
ce qui s'oppose a force gravitationnelle ($F_g$) avec a masse d'un objet flottant ($M_s$) selon :
| $ F_g = m_g g $ |
donc, avec ERROR:8663 et a masse d'un objet flottant ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
nous avons :
| $ M_b = M_s $ |
(ID 11955)
(ID 11966)
(ID 11968)
Puisque le principe d'Archim de stipule que ERROR:8663 est gal a masse d'un objet flottant ($M_s$),
| $ M_b = M_s $ |
nous avons ERROR:8663 li a densité du liquide ($\rho_w$), le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$) comme suit :
| $ M_b =4 a b d \rho_w $ |
et a masse d'un objet flottant ($M_s$) li a densité des objets ($\rho_s$), le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$) comme suit :
| $ M_s =8 a b c \rho_s $ |
ce qui implique que
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
(ID 11972)
(ID 11974)
Pour que le parall l pip de soit stable, a hauteur du métacentre ($z_M$) doit toujours tre sup rieur ou gal a hauteur du centre de masse ($z_G$), c'est- -dire
| $ z_M \geq z_G $ |
Par cons quent, avec a hauteur du centre de masse ($z_G$) tant le point d'application de la force de flottaison donn e avec a mi-hauteur du parallélépipède ($c$) et le brouillon d'objet ($d$) :
| $ z_G = c - d $ |
et a hauteur du métacentre ($z_M$) tant avec le demi-largeur du parallélépipède ($b$) :
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
nous obtenons a condition de stabilité d'un corps flottant ($e$) :
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
(ID 11975)
Exemples
(ID 15481)
Le navire de guerre su dois Vasa est un exemple connu d'un navire instable. Le 10 ao t 1628, seulement 20 minutes apr s avoir quitt le chantier naval lors de son voyage inaugural dans le port de Stockholm, le navire a chavir et a coul :

La conception du navire tait d fectueuse, car sa construction troite visait atteindre des vitesses lev es et sa structure haute tait destin e accueillir 64 canons, un nombre significatif. Cependant, cette conception rendait le navire intrins quement instable, ce qui a entra n son chavirement avec la premi re rafale de vent.
Heureusement, le navire a coul dans des eaux peu profondes et a t conserv dans l\'eau sal e pendant 333 ans jusqu\' sa r cup ration en 1961. Au d but, le navire a t maintenu mouill , puis lentement remplac l\'eau par un m lange de cire qui permet de l\'exposer compl tement sec dans un mus e quelques m tres de l\'endroit o il a coul .
Le Vasa sert de rappel dans la construction navale, d montrant l\'importance d\'une conception soigneuse et de la stabilit . Son exposition au mus e est une attraction populaire, attirant des visiteurs du monde entier pour voir cette pi ce remarquable de l\'histoire maritime.
(ID 11977)
Le point d'application de la force de pouss e est gal au centre de masse du volume de liquide d plac :

Dans un bateau de profil carr typique, cela correspond un point situ mi-profondeur (profondeur d\'immersion).
(ID 11957)
Lorsqu'une force lat rale est appliqu e et que l\'objet est inclin , on peut observer que le point o la force de flottaison agit se d place hors de l\'axe. En tra ant une ligne verticale depuis cette nouvelle position, on obtient que la ligne croise l\'axe central en un point appel le m tacentre :

(ID 11959)
La gravit agit sur le centre de masse, qui se trouve g n ralement au-dessus du point d'application de la force de flottabilit , mais peut tre au-dessus ou en dessous du m tacentre :

(ID 11960)
Si le m tacentre est situ au-dessus du centre de masse, la force de gravit g n re un couple qui a tendance stabiliser l'objet. C\'est comme si l\'objet tait suspendu au m tacentre et que la force de gravit g n re des rotations autour de celui-ci. Lorsque le centre de masse est situ en dessous du m tacentre, le couple g n re une rotation vers l\'axe, c\'est- -dire qu\'il a tendance corriger l\'inclinaison, stabilisant ainsi l\'objet :

(ID 11961)
Si le m tagcentre peut tre situ au-dessus ou en dessous du centre de gravit . Ce dernier peut facilement se produire si une charge est ajout e sur la partie sup rieure, faisant ainsi monter le centre de masse, ce qui rend le syst me instable.

Note : pour viter de perdre la stabilit , il est important de positionner la charge dans une position basse (fond du bateau).
(ID 11962)
Si le m tacentre est situ en dessous du centre de masse, la force de gravit g n re un couple qui a tendance d stabiliser l'objet. C\'est comme si l\'objet tait suspendu au m tacentre et que la force de gravit g n re des rotations autour de celui-ci. Lorsque le centre de masse est situ au-dessus du m tacentre, le couple g n re une rotation qui l\' loigne de l\'axe, c\'est- -dire qu\'il a tendance augmenter l\'inclinaison et donc d stabiliser l\'objet :

(ID 11963)
Le mod le de la coque du navire est r duit un parall l pip de avec des longueurs de le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$), ce qui donne des dimensions de $2a \times 2b \times 2c$, avec un tirant d'eau de un brouillon d'objet ($d$) :

(ID 11969)
Un mod le couramment utilis pour les bateaux est celui d'un parall l pip de droit avec des longueurs de le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$), et un centre de masse son centre g om trique. Lorsqu'il est plac dans l'eau, le corps s'enfonce jusqu' une profondeur de un brouillon d'objet ($d$). La position du centre o la force de flottaison agit peut tre vue dans l'image suivante, avec les coordonn es a hauteur du point d'attaque, force de flottabilité ($z_B$), a hauteur du centre de masse ($z_G$) et a hauteur du métacentre ($z_M$) :

Donc a hauteur du centre de masse ($z_G$) est
| $ z_G = c - d $ |
(ID 11964)
Le m tacentre est calcul en d terminant le centre de masse du corps inclin sous la condition que la surface situ e sous la ligne de flottaison (ligne bleue) reste constante :

(ID 11979)
Lorsque le bateau g te, une plus grande section deau se d place dun c t et la m me plus petite section du c t oppos . Le centre de masse est donc d plac du centre vers le secteur de plus grand d placement, qui est calcul par
$\bar{x} = \displaystyle\frac{\displaystyle\sum_i m_i x_i}{\displaystyle\sum_i m_i}$
La masse est proportionnelle la section calcul e partir de le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$) parxa0:
$2b d$
Toutes les masses d cal es des deux c t s de l'axe ne contribuent pas au num rateur et seuls les deux triangles indiqu s partir d'une zone avec le angle de gîte ($\phi$)
$b^2\phi$
pond rer la position du centre de masse des triangles
$\displaystyle\frac{2b}{3}$
ce que l'on voit sur le graphique :

Par cons quent, la distance au centre de masse de leau d plac e par rapport laxe est
$\displaystyle\frac{\displaystyle\frac{2b}{3} b^2\phi}{2bd}=\displaystyle\frac{b^2\phi}{3d}$
(ID 14248)
Si un navire g te le angle de gîte ($\phi$), le centre de masse de l'eau d plac e se d place avec le demi-largeur du parallélépipède ($b$) et le demi-longueur du parallélépipède ($a$) sur une distance dexa0:
$\displaystyle\frac{b^2\phi}{3d}$
Puisque cette distance est l'arc de cercle que l'on peut tracer autour du m tacentre, la distance entre le m tacentre et le centre de masse de l'eau d plac e, qui correspond au rayon, est :
$\displaystyle\frac{b^2}{3d}$
Par cons quent, la position du m tacentre doit tenir compte du fait que le centre de coordonn es est la hauteur de la surface de l'eau, soit une distance $d/2$ au-dessus du centre de masse de l'eau d plac e :

avec a hauteur du métacentre ($z_M$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
(ID 11967)
Pour que le parall l pip de soit stable, a hauteur du métacentre ($z_M$) doit toujours tre sup rieur ou gal a hauteur du centre de masse ($z_G$), c'est- -dire
| $ z_M \geq z_G $ |
Par cons quent, avec a hauteur du centre de masse ($z_G$) tant le point d'application de la force de flottaison donn e avec a mi-hauteur du parallélépipède ($c$) et le brouillon d'objet ($d$) :
| $ z_G = c - d $ |
et a hauteur du métacentre ($z_M$) tant avec le demi-largeur du parallélépipède ($b$) :
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
nous obtenons a condition de stabilité d'un corps flottant ($e$) :
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
ce qui signifie qu'il y a une r gion dans le graphe $b/c$ (largeur/profondeur) versus $d/2c$ (profondeur/hauteur) dans laquelle le syst me est stable, et dans son compl ment, instable :

En d'autres termes, la stabilit est obtenue avec des valeurs lev es de $b/c$ (largeur sup rieure au tirant d'eau). Dans le cas du navire Vasa, le probl me tait que le navire tait trop haut pour sa largeur. Une solution aurait t de "l'enfoncer plus profond ment" ou d'atteindre une valeur $d/c$ plus lev e pour viter la zone d'instabilit . Cependant, cela n' tait pas possible en raison des ouvertures pour les canons par lesquelles l'eau aurait pu entrer.
Pour plus d'informations sur les erreurs de construction, consultez Pourquoi le Vasa a coul xa0: 10 probl mes et quelques antidotes pour les projets logiciels, Richard E. Fairley, Mary Jane Willshire, mars/avril 2003 IEEE LOGICIEL, qui s'applique aux projets logiciels.
(ID 11976)
En tudiant les plans du Vasa, il est possible d\'estimer les coefficients de la relation entre la largeur et la hauteur, ainsi que entre le tirant d\'eau et la hauteur. Cette analyse r v le que le navire est instable:

(ID 14247)
(ID 15483)
Si a force de poussée ($F_b$) et a force gravitationnelle ($F_g$) sont gaux, l'objet flottera. Dans ce cas, cela signifie que a masse d'un objet flottant ($M_s$) doit tre gal ERROR:8663, ce qui donne :
| $ M_b = M_s $ |
Note : cette relation n'est possible que si l'objet 'p se moins que l'eau', ce qui signifie que l'eau d plac e occupe un volume gal ou sup rieur celui de l'objet.
(ID 11955)
A masse d'un objet flottant ($M_s$) peut tre calcul partir de a densité des objets ($\rho_s$) et du volume donn par ses param tres g om triques le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et a mi-hauteur du parallélépipède ($c$).
Par cons quent :
| $ M_s =8 a b c \rho_s $ |
(ID 11970)
ERROR:8663 peut tre calcul partir de a densité du liquide ($\rho_w$) et du volume donn par ses param tres g om triques le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$).
Donc :
| $ M_b =4 a b d \rho_w $ |
(ID 11971)
Le volume déplacé ($V_b$) peut tre calcul partir de ses param tres g om triques le demi-longueur du parallélépipède ($a$), le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$).
Donc:
| $ V_b = 4 a b d $ |
(ID 11968)
Le principe d'Archim de tablit que la masse d'eau d plac e est gale la masse de l'objet. Pour le cas sp cifique du parall l pip de rectangle, cela peut tre exprim comme a densité des objets ($\rho_s$), a densité du liquide ($\rho_w$), le brouillon d'objet ($d$) et a mi-hauteur du parallélépipède ($c$) de la mani re suivante :
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
(ID 11972)
Le point d'application de la force de flottaison se trouve au centre de masse du volume d\'eau d plac par le bateau. Dans le cas o le bateau n\'est pas inclin (escor ), ce point se situe au centre du volume mi-hauteur du tirant d\'eau.
En tenant compte de cela, vous pouvez exprimer a hauteur du point d'attaque, force de flottabilité ($z_B$) en fonction de le brouillon d'objet ($d$) soitxa0:
| $ z_B =-\displaystyle\frac{ d }{2}$ |
(ID 11965)
Le point d'application de la force gravitationnelle correspond au centre du parall l pip de qui mod lise la coque. Si nous fixons le syst me de coordonn es sur la surface de l'eau, a hauteur du centre de masse ($z_G$) sera donn en soustrayant le brouillon d'objet ($d$) de a mi-hauteur du parallélépipède ($c$) :
| $ z_G = c - d $ |
(ID 11966)
Le calcul de a hauteur du métacentre ($z_M$) partir de la distance entre le m tacentre et le centre de masse de l'eau d plac e, exprim e par le demi-largeur du parallélépipède ($b$) et le brouillon d'objet ($d$), est effectu comme suit:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
(ID 11973)
Pour que l'objet soit stable, a hauteur du métacentre ($z_M$) doit toujours tre sup rieur ou gal a hauteur du centre de masse ($z_G$).
Par cons quent, cela doit tre :
| $ z_M \geq z_G $ |
(ID 11974)
Pour un parall l pip de rectangle, a condition de stabilité d'un corps flottant ($e$) avec le demi-largeur du parallélépipède ($b$), a mi-hauteur du parallélépipède ($c$) et le brouillon d'objet ($d$) est :
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
ce qui est sup rieur un dans le cas d'une situation stable et n gatif dans le cas d'une instabilit .
(ID 11975)
ID:(1610, 0)
