Frenagem de pouso
Imagem 
Os aviões utilizam três mecanismos para frear durante o pouso:
• Reversão de empuxo, que redireciona o impulso dos motores para a frente em vez de para trás.
• Spoilers nas asas, que aumentam o coeficiente de resistência, expondo uma superfície ao fluxo de ar.
• Freios convencionais nas rodas.
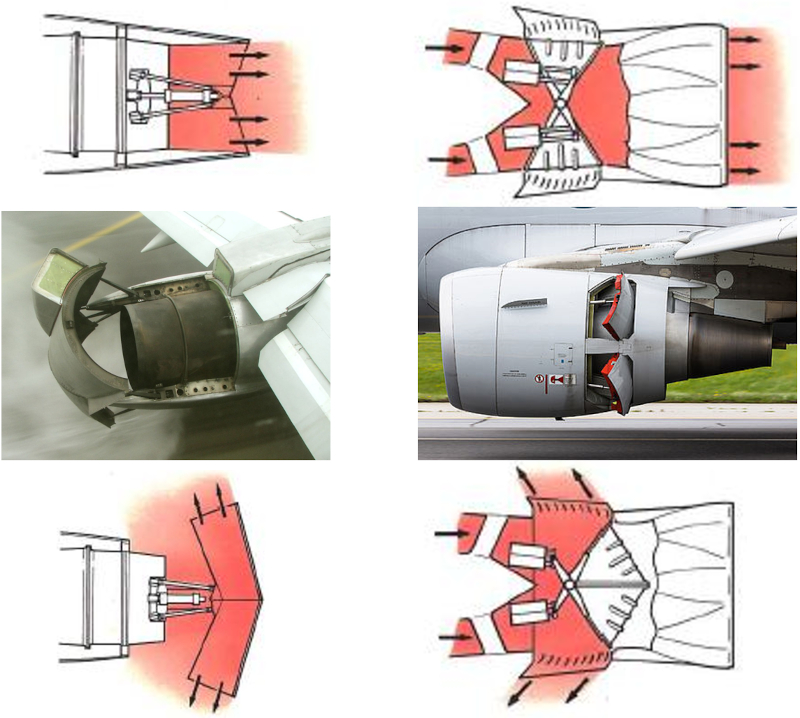
[1] Review of Thrust Reverser Mechanism used in Turbofan Jet Engine Aircraft, Mohd Anees Siddiqui, Md Shakibul Haq, International Journal of Engineering Research and Technology, Volume 6, Number 5 (2013), pp. 717-726, diagramas [2] Michael Fabry, F-GHXX Boeing 737-2A1(Adv) Alguma ação de reversão de empuxo durante um dia muito chuvoso, (jetphotos.com) - centro, esquerda [3] N90024 American Airlines Airbus A319-115(WL), AIRCANADA087, (planespotters.net) - centro, direita
Na imagem abaixo, podem ser observados dois tipos de reversores de empuxo: o primeiro utiliza um defletor movido no fluxo de ar que sai do motor, enquanto o segundo direciona o próprio fluxo de ar para a frente.
ID:(14476, 0)
Pouso
Descrição 
A chave para aterrissar é modificar a asa de forma a obter sustentação suficiente em velocidades mais baixas, permitindo uma descida controlada para alcançar a pista e conseguir parar a aeronave na pista disponível.
Variáveis
Cálculos
Cálculos
Equações
De maneira semelhante forma como a equa o para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) ser equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no c lculo de la força de resistência ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
O coeficiente de arrasto medido e, em fluxos turbulentos sobre corpos aerodin micos, geralmente se obt m valores em torno de 0.4.
(ID 4418)
Se igualarmos la força de propulsão ($F_p$) com la força de resistência ($F_W$) com o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) em
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v_L ^2$ |
obtemos, para uma la velocidade máxima ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
o que, quando resolvido para a velocidade m xima, resulta em
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
(ID 14507)
Com a equa o para la velocidade em relação ao meio ($v$) em o hora de decolagem ($t$) com la aceleração máxima ($a_p$) e la velocidade máxima ($v_p$):
| $\displaystyle\frac{dv}{dt}=-a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
ela pode ser integrada a partir de um valor inicial de la velocidade de pouso ($v_L$)
$\displaystyle\int_{v_L}^v \displaystyle\frac{dv}{1 - v^2/v_p^2} = -\displaystyle\int_0^t dt a_p$
e com a defini o de o tempo de propulsão de decolagem/pouso ($\tau_p$)
| $ \tau_p = \displaystyle\frac{ v_p }{ a_p }$ |
o resultado
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
(ID 14511)
Com a equa o ERROR:6110,0 usando la velocidade de pouso ($v_L$), la velocidade máxima ($v_p$), o tempo de propulsão de decolagem/pouso ($\tau_p$) e o hora de decolagem ($t$) da seguinte forma:
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
onde em o hora de decolagem ($t$) igual a o tempo de pouso ($t_L$), temos:
$v = v_L - v_p \tan\left(\displaystyle\frac{t_L}{\tau_p}\right)=0$
Se resolvermos esta equa o para o tempo, obtemos:
| $ t_L = \tau_p \arctan\left(\displaystyle\frac{ v_L }{ v_p }\right)$ |
(ID 14513)
Dado que la velocidade em relação ao meio ($v$) durante o pouso varia em fun o de o hora de decolagem ($t$) com la velocidade de pouso ($v_L$), la velocidade máxima ($v_p$) e o tempo de propulsão de decolagem/pouso ($\tau_p$) de acordo com a seguinte equa o:
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
ela igual a o caminho percorrido na pista ($s$) como fun o de o hora de decolagem ($t$).
Podemos integrar a equa o:
$\displaystyle\frac{ds}{dt}=v_0-v_p\tan\left(\displaystyle\frac{t}{\tau_p}\right)$
Obtendo assim o caminho como:
$s = v_L t + \log(|\cos( t / \tau_p)|) v_p \tau_p$
Se o hora de decolagem ($t$), o fator logar tmico pode ser expandido at a terceira ordem, resultando no caminho de pouso sendo igual a:
| $ s = \left( v_L - a_p \displaystyle\frac{ t }{2}\right) t $ |
(ID 14514)
Exemplos
(ID 15174)
Os avi es utilizam tr s mecanismos para frear durante o pouso:
• Revers o de empuxo, que redireciona o impulso dos motores para a frente em vez de para tr s.
• Spoilers nas asas, que aumentam o coeficiente de resist ncia, expondo uma superf cie ao fluxo de ar.
• Freios convencionais nas rodas.

[1] Review of Thrust Reverser Mechanism used in Turbofan Jet Engine Aircraft, Mohd Anees Siddiqui, Md Shakibul Haq, International Journal of Engineering Research and Technology, Volume 6, Number 5 (2013), pp. 717-726, diagramas [2] Michael Fabry, F-GHXX Boeing 737-2A1(Adv) Alguma a o de revers o de empuxo durante um dia muito chuvoso, (jetphotos.com) - centro, esquerda [3] N90024 American Airlines Airbus A319-115(WL), AIRCANADA087, (planespotters.net) - centro, direita
Na imagem abaixo, podem ser observados dois tipos de reversores de empuxo: o primeiro utiliza um defletor movido no fluxo de ar que sai do motor, enquanto o segundo direciona o pr prio fluxo de ar para a frente.
(ID 14476)
(ID 15187)
La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte f rmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
(ID 4418)
No in cio da decolagem, a resist ncia aerodin mica, que depende da velocidade, m nima. Portanto, la aceleração máxima ($a_p$) determinada unicamente por la força de propulsão ($F_p$) e la massa corporal ($m$):
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
medida que a resist ncia aerodin mica comece a reduzir a for a de propuls o, essa acelera o inicial ser a m xima poss vel.
(ID 14506)
La força de propulsão ($F_p$) contrabalan a la força de resistência ($F_W$) gerando velocidade, o que, por sua vez, aumenta a mesma for a de resist ncia, conforme descrito em o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) em
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v_L ^2$ |
Esse processo continua a aumentar a velocidade at o ponto em que a for a de propuls o iguala a for a de resist ncia, representando a velocidade m xima alcan vel.
Ao igualar a for a de propuls o com a for a de resist ncia e resolver para a velocidade, obtemos la velocidade máxima ($v_p$):
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
medida que a resist ncia aerodin mica come a a reduzir a for a de propuls o, essa acelera o inicial ser a m xima poss vel.
(ID 14507)
Com a acelera o gerada pelos motores, representada por
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
e a velocidade m xima associada resist ncia, descrita por
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
podemos definir um tempo caracter stico usando a seguinte express o:
| $ \tau_p = \displaystyle\frac{ v_p }{ a_p }$ |
Este tempo fornece uma estimativa da ordem de grandeza do processo de decolagem e aterrissagem, que geralmente ocorre em quest o de minutos.
(ID 14510)
A equa o para calcular la velocidade em relação ao meio ($v$) em o hora de decolagem ($t$) com la aceleração máxima ($a_p$) e la velocidade máxima ($v_p$) a seguinte:
| $\displaystyle\frac{dv}{dt}=-a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
Ap s a integra o, obt m-se o tempo de propulsão de decolagem/pouso ($\tau_p$) e la velocidade de pouso ($v_L$).
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
No in cio, quando o tempo muito menor que o tempo caracter stico, a tangente pode ser substitu da pelo seu argumento. Isso implica que a velocidade diminui principalmente devido influ ncia dos motores.
(ID 14511)
A equa o para ERROR:6110,0 de uma aeronave durante o pouso dada com la velocidade de pouso ($v_L$), la velocidade máxima ($v_p$), o tempo de propulsão de decolagem/pouso ($\tau_p$) e o hora de decolagem ($t$) da seguinte forma:
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
Portanto, o tempo de pouso ($t_L$) calculado usando esta equa o para o caso em que a velocidade naquele momento zero. Isso se traduz em:
| $ t_L = \tau_p \arctan\left(\displaystyle\frac{ v_L }{ v_p }\right)$ |
(ID 14513)
Dado que la velocidade em relação ao meio ($v$) durante o pouso varia em rela o a o hora de decolagem ($t$) com la velocidade de pouso ($v_L$), la velocidade máxima ($v_p$) e o tempo de propulsão de decolagem/pouso ($\tau_p$) de acordo com a seguinte equa o:
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
podemos calcular a dist ncia percorrida ao longo da pista integrando esta equa o ao longo do tempo:
| $ s = \left( v_L - a_p \displaystyle\frac{ t }{2}\right) t $ |
A equa o resultante uma aproxima o de terceira ordem de $t/\tau_p$, o que significa que as ajudas aerodin micas para a frenagem s o significativamente reduzidas em compara o com a revers o de impulso dos motores.
Al m disso, podemos usar o tempo de aterrizagem para estimar o comprimento da pista necess rio para a aterrissagem.
(ID 14514)
O pouso termina quando la velocidade em relação ao meio ($v$) se torna zero, o que implica que o tempo ($t$) igual a o tempo de pouso ($t_L$), resultando na redu o de o caminho percorrido na pista ($s$) para o distância de pouso ($s_L$). Portanto, com la aceleração máxima ($a_p$) e la velocidade de pouso ($v_L$), obt m-se:
| $ s_L = \left( v_L - a_p \displaystyle\frac{ t_L }{2}\right) t_L $ |
(ID 15997)
ID:(1968, 0)
