L'atterrissage
Storyboard 
La clé de l'atterrissage consiste à modifier l'aile de manière à obtenir une portance suffisante à des vitesses plus basses, ce qui permet une descente contrôlée pour atteindre la piste et arrêter l'aéronef sur la piste disponible.
ID:(1968, 0)
Freinage à l'atterrissage
Image 
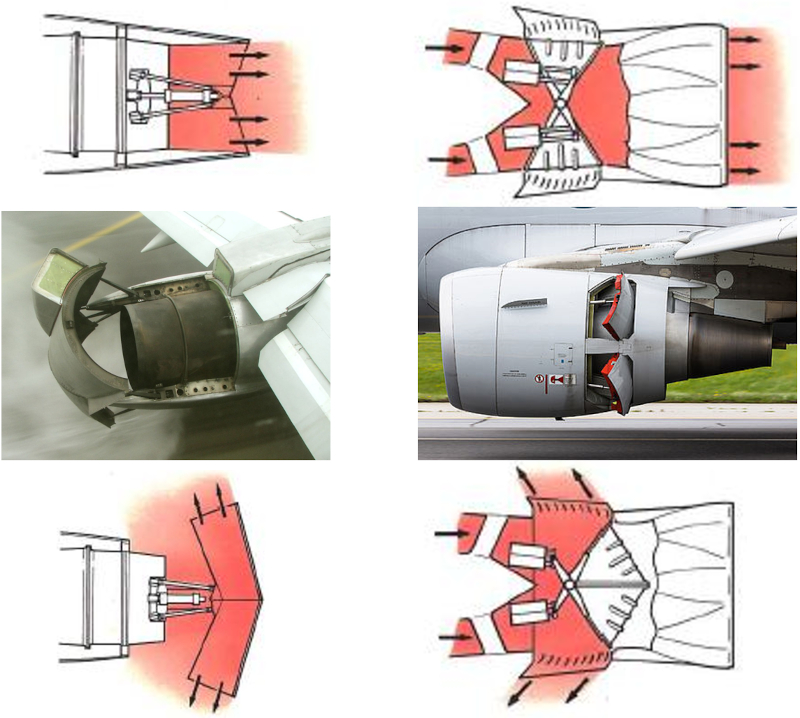
Les avions utilisent trois mécanismes pour freiner lors de l'atterrissage :
• L'inversion de poussée, qui redirige la poussée des moteurs vers l'avant au lieu de l\'arrière.
• Les spoilers sur les ailes, qui augmentent le coefficient de traînée en exposant une surface au flux d'air.
• Les freins conventionnels sur les roues.
[1] Review of Thrust Reverser Mechanism used in Turbofan Jet Engine Aircraft, Mohd Anees Siddiqui, Md Shakibul Haq, International Journal of Engineering Research and Technology, Volume 6, Number 5 (2013), pp. 717-726, schémas [2] Michael Fabry, F-GHXX Boeing 737-2A1(Adv) Some reverse thrust action during a very rainy day, (jetphotos.com) - centre, gauche [3] N90024 American Airlines Airbus A319-115(WL), AIRCANADA087, (planespotters.net) - centre, droite
Sur l'image ci-dessous, on peut voir deux types d\'inverseurs de poussée : le premier utilise un déflecteur mobile dans le flux d'air sortant du moteur, tandis que le second redirige lui-même le flux d'air vers l'avant.
ID:(14476, 0)
L'atterrissage
Description 
La clé de l'atterrissage consiste à modifier l'aile de manière à obtenir une portance suffisante à des vitesses plus basses, ce qui permet une descente contrôlée pour atteindre la piste et arrêter l'aéronef sur la piste disponible.
Variables
Calculs
Calculs
Équations
De mani re similaire la fa on dont l' quation pour a force de levage ($F_L$) a t d riv e en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
dans cette analogie, ce qui correspond a surface génératrice de portance ($S_w$) sera quivalent le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Le coefficient de tra n e est mesur et, dans les coulements turbulents sur les corps a rodynamiques, les valeurs sont g n ralement autour de 0.4.
(ID 4418)
Si nous galons a force de propulsion ($F_p$) avec a force de résistance ($F_W$) avec le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) dans
nous obtenons, pour un a vitesse maximum ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
ce qui, lorsqu'on le r sout pour la vitesse maximale, donne
(ID 14507)
Avec l' quation pour a vitesse par rapport au milieu ($v$) en le heure de décollage ($t$) avec a accélération maximale ($a_p$) et a vitesse maximum ($v_p$) :
| $\displaystyle\frac{dv}{dt}=-a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
elle peut tre int gr e partir d'une valeur initiale de a vitesse d'atterrissage ($v_L$)
$\displaystyle\int_{v_L}^v \displaystyle\frac{dv}{1 - v^2/v_p^2} = -\displaystyle\int_0^t dt a_p$
et avec la d finition de le temps de propulsion décollage/atterrissage ($\tau_p$)
| $ \tau_p = \displaystyle\frac{ v_p }{ a_p }$ |
le r sultat est
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
(ID 14511)
Avec l' quation ERROR:6110,0 utilisant a vitesse d'atterrissage ($v_L$), a vitesse maximum ($v_p$), le temps de propulsion décollage/atterrissage ($\tau_p$) et le heure de décollage ($t$) comme suit :
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
o en le heure de décollage ($t$) est gal le temps d'atterrissage ($t_L$), nous avons :
$v = v_L - v_p \tan\left(\displaystyle\frac{t_L}{\tau_p}\right)=0$
Si nous r solvons cette quation pour le temps, nous obtenons :
| $ t_L = \tau_p \arctan\left(\displaystyle\frac{ v_L }{ v_p }\right)$ |
(ID 14513)
tant donn que a vitesse par rapport au milieu ($v$) lors de l'atterrissage varie en fonction de le heure de décollage ($t$) avec a vitesse d'atterrissage ($v_L$), a vitesse maximum ($v_p$) et le temps de propulsion décollage/atterrissage ($\tau_p$) selon l' quation suivante :
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
elle est gale le chemin parcouru sur la piste ($s$) en fonction de le heure de décollage ($t$).
Nous pouvons int grer l' quation :
$\displaystyle\frac{ds}{dt}=v_0-v_p\tan\left(\displaystyle\frac{t}{\tau_p}\right)$
pour obtenir le chemin comme suit :
$s = v_L t + \log(|\cos( t / \tau_p)|) v_p \tau_p$
Si le heure de décollage ($t$), le facteur logarithmique peut tre d velopp jusqu'au troisi me ordre, ce qui fait que le chemin d'atterrissage est gal :
| $ s = \left( v_L - a_p \displaystyle\frac{ t }{2}\right) t $ |
(ID 14514)
Exemples
(ID 15174)
Les avions utilisent trois m canismes pour freiner lors de l'atterrissage :
• L'inversion de pouss e, qui redirige la pouss e des moteurs vers l'avant au lieu de l\'arri re.
• Les spoilers sur les ailes, qui augmentent le coefficient de tra n e en exposant une surface au flux d'air.
• Les freins conventionnels sur les roues.

[1] Review of Thrust Reverser Mechanism used in Turbofan Jet Engine Aircraft, Mohd Anees Siddiqui, Md Shakibul Haq, International Journal of Engineering Research and Technology, Volume 6, Number 5 (2013), pp. 717-726, sch mas [2] Michael Fabry, F-GHXX Boeing 737-2A1(Adv) Some reverse thrust action during a very rainy day, (jetphotos.com) - centre, gauche [3] N90024 American Airlines Airbus A319-115(WL), AIRCANADA087, (planespotters.net) - centre, droite
Sur l'image ci-dessous, on peut voir deux types d\'inverseurs de pouss e : le premier utilise un d flecteur mobile dans le flux d'air sortant du moteur, tandis que le second redirige lui-m me le flux d'air vers l'avant.
(ID 14476)
(ID 15187)
A force de résistance ($F_W$) peut tre calcul en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
(ID 4418)
Au d but du d collage, la r sistance a rodynamique, qui d pend de la vitesse, est minimale. Par cons quent, a accélération maximale ($a_p$) est d termin e uniquement par a force de propulsion ($F_p$) et a masse corporelle ($m$) :
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
mesure que la r sistance a rodynamique commence r duire la force de propulsion, cette acc l ration initiale sera maximale.
(ID 14506)
A force de propulsion ($F_p$) contrebalance a force de résistance ($F_W$) en g n rant de la vitesse, ce qui son tour augmente la m me force de r sistance, comme d crit dans le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) dans
Ce processus continue d'augmenter la vitesse jusqu'au point o la force de propulsion quivaut la force de r sistance, ce qui repr sente la vitesse maximale atteignable.
En galant la force de propulsion la force de r sistance et en r solvant pour la vitesse, nous obtenons a vitesse maximum ($v_p$) :
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
mesure que la r sistance a rodynamique commence r duire la force de propulsion, cette acc l ration initiale sera maximale.
(ID 14507)
Avec l'acc l ration g n r e par les moteurs, repr sent e par
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
et la vitesse maximale associ e la r sistance, d crite par
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
nous pouvons d finir un temps caract ristique en utilisant l'expression suivante :
| $ \tau_p = \displaystyle\frac{ v_p }{ a_p }$ |
Ce temps fournit une estimation de l'ordre de grandeur du processus de d collage et d'atterrissage, qui se d roule g n ralement en quelques minutes.
(ID 14510)
L' quation permettant de calculer a vitesse par rapport au milieu ($v$) en le heure de décollage ($t$) avec a accélération maximale ($a_p$) et a vitesse maximum ($v_p$) est la suivante :
| $\displaystyle\frac{dv}{dt}=-a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
Lorsqu'on l'int gre, on obtient le temps de propulsion décollage/atterrissage ($\tau_p$) et a vitesse d'atterrissage ($v_L$).
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
Au d but, lorsque le temps est nettement inf rieur au temps caract ristique, on peut remplacer la tangente par son argument. Cela signifie que la vitesse diminue principalement en raison de l'influence des moteurs.
(ID 14511)
L' quation pour ERROR:6110,0 d'un avion lors de l'atterrissage est donn e avec a vitesse d'atterrissage ($v_L$), a vitesse maximum ($v_p$), le temps de propulsion décollage/atterrissage ($\tau_p$) et le heure de décollage ($t$) comme suit :
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
Par cons quent, le temps d'atterrissage ($t_L$) est calcul en utilisant cette quation pour le cas o la vitesse ce moment est nulle. Cela se traduit par :
| $ t_L = \tau_p \arctan\left(\displaystyle\frac{ v_L }{ v_p }\right)$ |
(ID 14513)
tant donn que a vitesse par rapport au milieu ($v$) pendant l'atterrissage varie en fonction de le heure de décollage ($t$) avec a vitesse d'atterrissage ($v_L$), a vitesse maximum ($v_p$) et le temps de propulsion décollage/atterrissage ($\tau_p$) selon l' quation suivante :
| $ v = v_L - v_p \tan\left(\displaystyle\frac{ t }{ \tau_p }\right)$ |
nous pouvons calculer la distance parcourue le long de la piste en int grant cette quation dans le temps :
| $ s = \left( v_L - a_p \displaystyle\frac{ t }{2}\right) t $ |
L' quation r sultante est une approximation du troisi me ordre de $t/\tau_p$, ce qui signifie que les aides a rodynamiques la d c l ration sont consid rablement r duites par rapport la r version de la pouss e des moteurs.
De plus, nous pouvons utiliser le temps d'atterrissage pour estimer la longueur de piste n cessaire l'atterrissage.
(ID 14514)
L'atterrissage se termine lorsque a vitesse par rapport au milieu ($v$) devient nul, ce qui implique que le temps ($t$) est gal le temps d'atterrissage ($t_L$), entra nant une r duction de le chemin parcouru sur la piste ($s$) Le distance d'atterrissage ($s_L$). Par cons quent, avec a accélération maximale ($a_p$) et a vitesse d'atterrissage ($v_L$), on obtient :
| $ s_L = \left( v_L - a_p \displaystyle\frac{ t_L }{2}\right) t_L $ |
(ID 15997)
ID:(1968, 0)
