Benützer:
Arbeit
Storyboard 
Die Arbeit hängt davon ab, wie der Prozess abläuft. Zum Beispiel repräsentiert sie die Energie, die benötigt wird, um eine bestimmte Kraft aufzuwenden und einen Körper über eine bestimmte Distanz zu bewegen, oder den Druck, der auf ein Gas ausgeübt werden muss, damit es sich um ein bestimmtes Volumen ausdehnen kann.
ID:(1470, 0)
Mechanismen
Iframe
In der Thermodynamik ist Arbeit die Energie, die zu oder von einem System übertragen wird, indem eine Kraft über eine bestimmte Strecke wirkt. Dies kann in verschiedenen Formen erfolgen, wie mechanische Arbeit, bei der ein Gas in einem Zylinder mit einem Kolben expandiert und den Kolben bewegt, oder elektrische Arbeit, bei der Energie durch elektrische Kräfte übertragen wird. Das Konzept der Arbeit ist entscheidend für das Verständnis von Energieaustausch und Prozessen. Mathematisch wird es oft durch Druck- und Volumenänderungen im System dargestellt. Nach dem ersten Hauptsatz der Thermodynamik entspricht die Änderung der inneren Energie eines Systems der zugeführten Wärme minus der vom System geleisteten Arbeit. Arbeit ist integraler Bestandteil verschiedener Prozesse, einschließlich isothermer, adiabatischer, isobarer und isochorer Prozesse, und ist in Anwendungen wie Wärmekraftmaschinen und Kühlschränken wesentlich, wo sie eine Schlüsselrolle bei der Umwandlung von Wärme in Arbeit oder der Nutzung von Arbeit zur Wärmeübertragung spielt.
Mechanismen
ID:(15247, 0)
Umwandlung von Arbeit in Wärme
Beschreibung
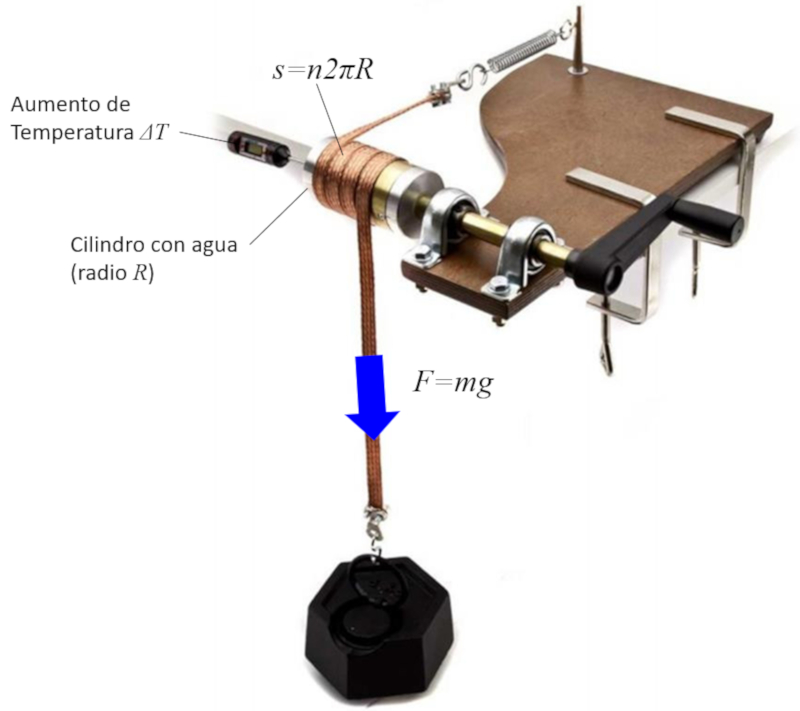
Die Umwandlung von Arbeit in Energie wird durch die Erzeugung von Wärme durch Reibung untersucht. Dazu wird ein Metallband um einen Zylinder gewickelt, der Wasser und ein Thermometer enthält. Durch Drehen der Kurbel entsteht durch Reibung Wärme, die zur Erwärmung des Wassers führt. Wenn die aufgebrachte Kraft, die Anzahl der Umdrehungen und der Radius des Zylinders gemessen werden, kann die zurückgelegte Strecke geschätzt werden, was wiederum die Energie als das Produkt aus Kraft und Strecke ermöglicht.
ID:(1884, 0)
Druck und Arbeit
Beschreibung
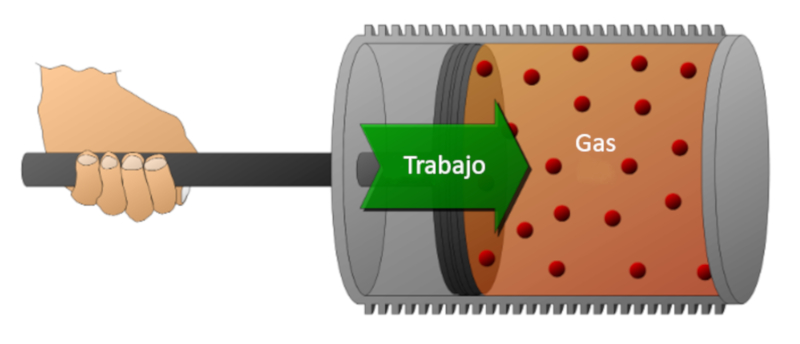
Betrachten wir ein Gas in einem Zylinder, in dem sich ein Kolben bewegen kann. Wenn der Kolben bewegt wird, kann das Gasvolumen durch Kompression verringert werden. Für diese Kompression wird Energie benötigt, die gleich der vom Gas ausgeübten Kraft multipliziert mit der zurückgelegten Strecke des Kolbens ist. Diese Energie kann auch in Bezug auf den Druck dargestellt werden, da Druck durch die Kraft und den Querschnitt des Kolbens definiert wird.
Arbeit kann am System geleistet werden (Kompression) oder vom System auf die externe Umgebung übertragen werden (Expansion).
Da die Mechanische Kraft ($F$) geteilt durch die Abschnitt ($S$) gleich die Druck ($p$) ist:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
und die Volumenvariation ($dV$) mit der Zurückgelegter Weg ($dx$) gleich ist:
| $ \Delta V = S \Delta s $ |
Die Gleichung für der Differential ungenaue Arbeits ($\delta W$) kann wie folgt ausgedrückt werden:
| $ \delta W = F dx $ |
Daher kann sie geschrieben werden als:
| $ \delta W = p dV $ |
ID:(11126, 0)
Druck und Arbeit an einem Gas
Beschreibung
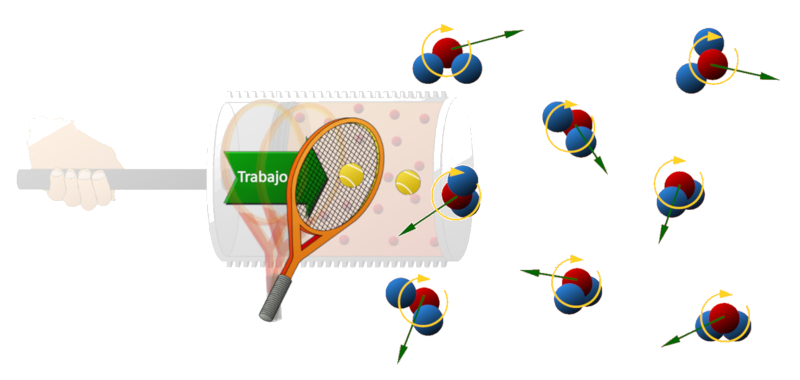
Wenn der Kolben sich im Zylinder bewegt, fungiert er wie ein Tennisschläger, der den Molekülen kinetische Energie verleiht und ihre Geschwindigkeit erhöht. Da diese Moleküle eine höhere Geschwindigkeit erreichen, übertragen sie einen größeren Impuls auf die Wände und erzeugen dadurch einen höheren Druck.
ID:(11127, 0)
Druck und Arbeit in einer Flüssigkeit/Feststoff
Beschreibung
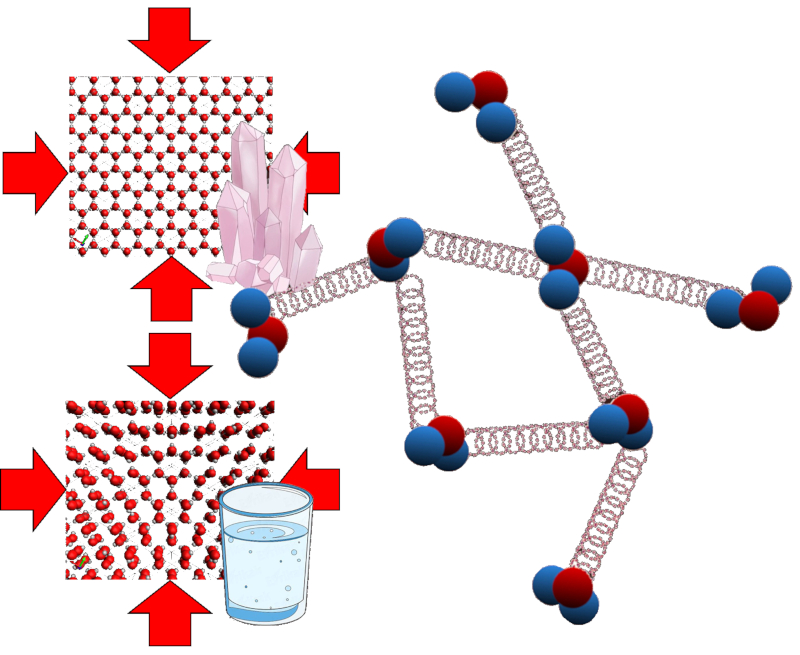
Im Fall einer Flüssigkeit oder eines Feststoffs verschiebt eine externe Kraft die Partikel des Materials, was die potenzielle Energie der Bindungen zwischen ihnen beeinflusst. Man kann sich das vorstellen, als würden kleine Federn zusammengedrückt werden, was ihre potenzielle Energie erhöht.
ID:(11128, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \delta W = F dx $
dW = F * dx
$ \delta W = p dV $
dW = p * dV
$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$
W = @INT( p , V , V_1 , V_2 )
ID:(15306, 0)
Arbeit
Gleichung
Die Beziehung zwischen Arbeit und unseren Handlungen hängt von der Abhängigkeit von der Differential ungenaue Arbeits ($\delta W$) von der zurückgelegten Strecke ab. Wenn wir eine Mechanische Kraft ($F$) in Betracht ziehen, um ein Objekt entlang von ein Zurückgelegter Weg ($dx$) zu bewegen, kann die benötigte Energie wie folgt ausgedrückt werden:
| $ \delta W = F dx $ |
Die Notation $\delta W$ wird verwendet, um die Veränderung der Arbeit anzugeben, im Gegensatz zu $dW$, was uns daran erinnert, dass ihr Wert vom Prozess der Veränderung der Länge $dx$ abhängt. Ein Beispiel hierfür wäre, wenn die Verschiebung in einem Gas erfolgen würde und eine Veränderung darin auftritt, in welchem Fall:
$\delta W < Fdx$
ID:(3202, 0)
Arbeit und Druck
Gleichung
Der Differential ungenaue Arbeits ($\delta W$) ist gleich die Druck ($p$) multipliziert mit die Volumenvariation ($dV$):
| $ \delta W = p dV $ |
Da die Mechanische Kraft ($F$) geteilt durch die Abschnitt ($S$) gleich die Druck ($p$) ist:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
und die Volumenvariation ($dV$) mit der Zurückgelegter Weg ($dx$) gleich ist:
| $ \Delta V = S \Delta s $ |
Die Gleichung für der Differential ungenaue Arbeits ($\delta W$) kann wie folgt ausgedrückt werden:
| $ \delta W = F dx $ |
Daher kann sie geschrieben werden als:
| $ \delta W = p dV $ |
ID:(3468, 0)
Arbeit erledigt
Gleichung
Der Effektive Arbeit ($W$) entspricht dem Integral von die Druck ($p$) bezüglich der Volumen ($V$) von $V_1$ bis $V_2$. Dies repräsentiert die von der Maschine geleistete Arbeit, die wie folgt ausgedrückt werden kann:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
ID:(10253, 0)
0
Video
Video: Arbeit