Storyboard

Das Trägheitsmoment ist der Drehfaktor, der der Masse in der Translation entspricht.

Das Trägheitsmoment kann empirisch bestimmt werden, indem ein Körper um eine Achse gedreht oder berechnet wird, wie sich die Masse um die Achse verteilt.

>Modell

ID:(600, 0)

Definition

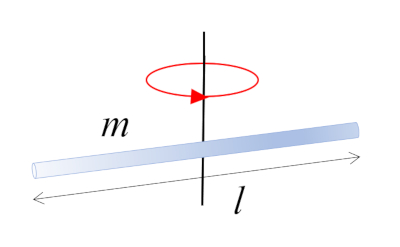
Ein Balken mit Masse $m$ und Länge $l$, der um sein Zentrum rotiert, das mit dem Schwerpunkt übereinstimmt:

ID:(10962, 0)

Bild

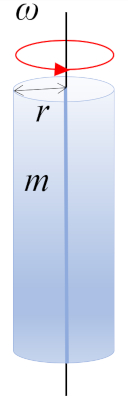
Die Drehung eines Zylinders mit Masse $m$ und Radius $r$ um die Achse des Zylinders, wobei sich der Schwerpunkt (CM) in halber Höhe befindet:

ID:(10964, 0)

Notiz

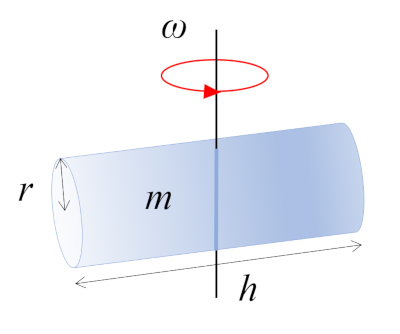
In dieser Situation rotiert ein Zylinder mit Masse $m$, Radius $r$ und Höhe $h$ um eine Achse, die senkrecht zu seiner eigenen Achse verläuft. Diese Achse verläuft durch den Mittelpunkt der Länge des Zylinders, wo sich der Schwerpunkt (CM) befindet:

ID:(10965, 0)

Zitat

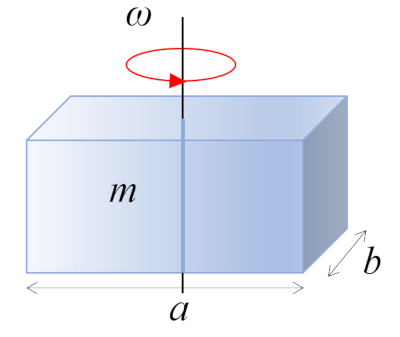
Ein rechtwinkliges Quader mit der Masse $m$ und den Seitenlängen $a$ und $b$, das senkrecht zur Rotationsachse steht, dreht sich um seinen Schwerpunkt, der sich im geometrischen Zentrum des Körpers befindet:

ID:(10973, 0)

Übung

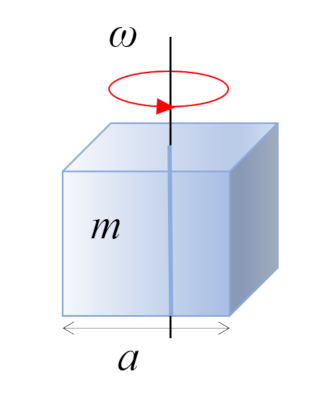
Im Fall eines rechtwinkligen Quaders mit Masse $m$ und Seitenlänge $a$ befindet sich der Schwerpunkt im geometrischen Zentrum:

ID:(10963, 0)

Gleichung

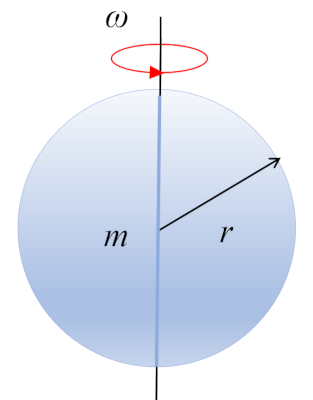
Eine Kugel mit der Masse $m$ und dem Radius $r$ rotiert um ihren Schwerpunkt, der sich im geometrischen Zentrum befindet:

ID:(10490, 0)