Usuario:


Producto Cruz o Producto Vectorial
Storyboard

El llamado producto cruz o producto vectorial permite determinar un vector ortogonal a los vectores que lo crean. Su magnitud corresponde al doble del area que tendria un rectangulo con lados iguales a las magnitudes de cada uno de los vectores.

>Modelo

ID:(1259, 0)


Representación gráfica del producto cruz
Definición

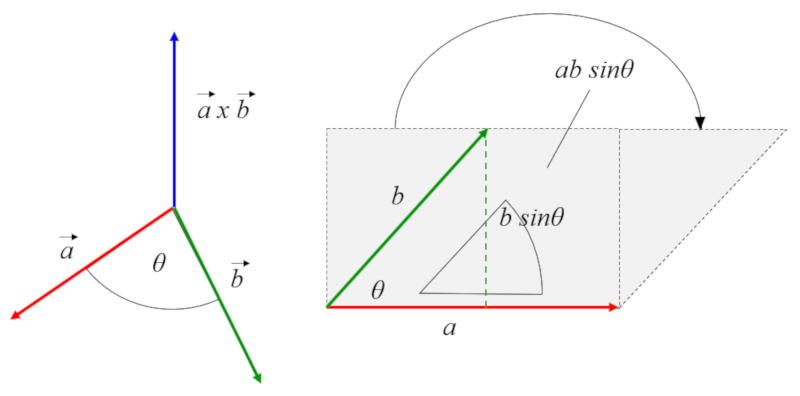
El producto cruz genera un vector que es ortogonal a aquellos que lo generan y cuya magnitud es la multiplicación de las magnitudes de cada vector y el seno del angulo entre ambos.

El largo del vector resultante corresponde al área del paralelepípedo que forman los dos vectores que lo generan:

ID:(4582, 0)


Producto Cruz o Producto Vectorial
Storyboard

El llamado producto cruz o producto vectorial permite determinar un vector ortogonal a los vectores que lo crean. Su magnitud corresponde al doble del area que tendria un rectangulo con lados iguales a las magnitudes de cada uno de los vectores.

Variables

Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\theta$
theta
Angulo entre los vectores
rad
$\mid\vec{a}\times\vec{b}\mid$
axb
Magnitud del producto cruz
-
$\mid\vec{a}\mid$
a
Magnitud del vector
m
$\mid\vec{b}\mid$
b
Magnitud del vector
m
$\vec{a}$
&a
Vector
m
$\vec{b}$
&b
Vector
m
$b_y$
b_y
Vector que resulta de la suma
m

Cálculos


Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

El producto cruz genera un vector que es ortogonal a aquellos que lo generan y cuya magnitud es la multiplicaci n de las magnitudes de cada vector y el seno del angulo entre ambos.

El largo del vector resultante corresponde al rea del paralelep pedo que forman los dos vectores que lo generan:

image

El producto cruz se puede definir como una determinante de una matriz cuyas lineas son los versores del sistema \hat{n}=(e_x,e_y,e_z), en la segunda y tercera l neas las coordenadas de los vectores \vec{a}=(a_x,a_y,a_z) y \vec{b}=(b_x,b_y,b_z) por lo que se obtiene un vector

equation

Si se expresa el producto cruz en funci n del versor \hat{e} ortogonal a los vectores \vec{a} y \vec{b} se tiene que

equation

donde \theta es el angulo entre ambos vectores.

>Modelo

ID:(1259, 0)