Caso: Carga del musculo en el tiempo
Storyboard 
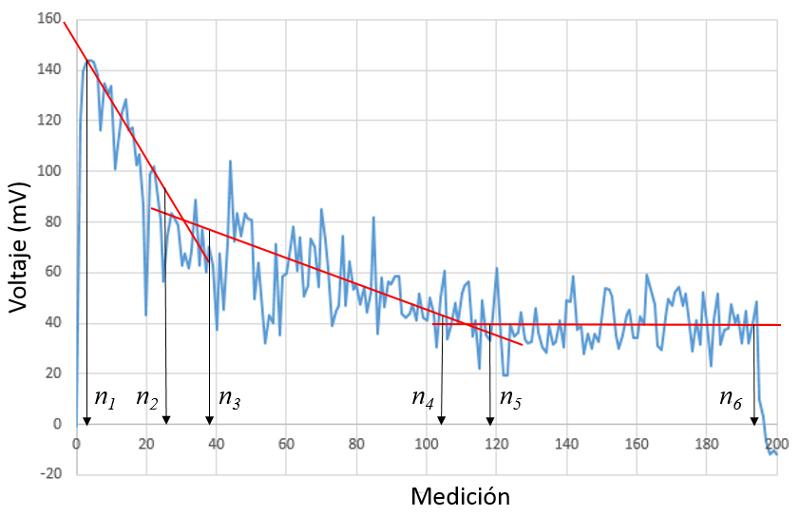
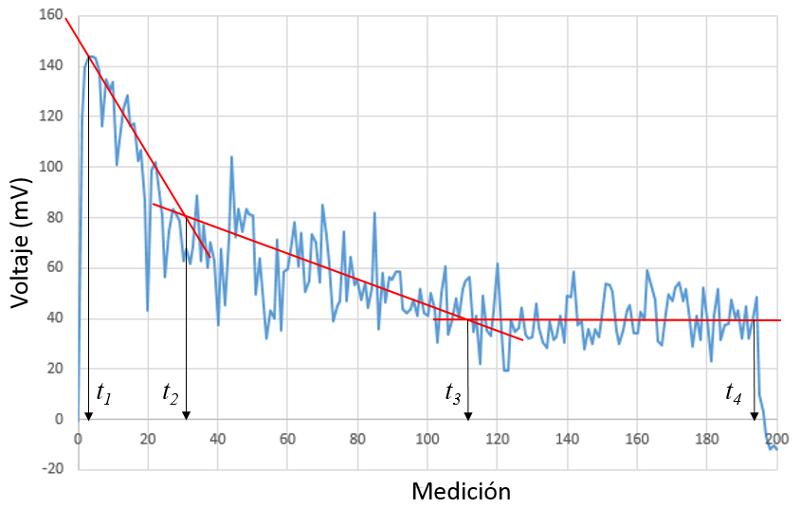
En el estudio se analiza la evolución de la fuerza en el tiempo para un experimento en que la persona intenta con el biceps mantener el máximo de fuerza posible. Dentro del experimento se ve que la fuerza decrece por fatiga mostrando la existencia de tres etapas en el tiempo.
ID:(63, 0)
Fuerza del musculo y fatiga
Definición 
El ejercicio se realiza durante 8 minutos en que la persona debe tratar de mantener la mayor fuerza que le sea posible. En la siguiente imagen se muestra como se realiza la fuerza y se indica una curva fuerza vs tiempo a modo de ejemplo:
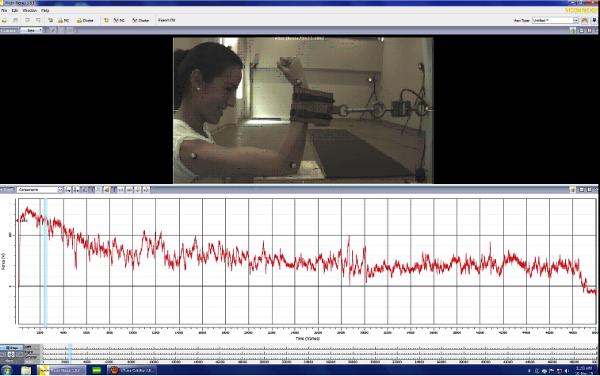
Ejercicio de fatiga
Los datos resumidos (201 en vez 500050 puntos) se pueden bajar desde
[ muscle_data.xlsx](http://www.gphysics.net/downloads/uach/kinesiologia/muscle_data.xlsx)
muscle_data.xlsx](http://www.gphysics.net/downloads/uach/kinesiologia/muscle_data.xlsx)
ID:(2486, 0)
Cálculos de las energías y potencias
Ejercicio 
Finalmente se puede estimar con el modelo del musculo la sección.
Con los parámetros microscópicos de la estructura del músculo se puede estimar la potencia para las fuerzas máximas de cada fase y la energía consumida en cada una de estas.
ID:(1327, 0)
Caso: Carga del musculo en el tiempo
Storyboard 
En el estudio se analiza la evolución de la fuerza en el tiempo para un experimento en que la persona intenta con el biceps mantener el máximo de fuerza posible. Dentro del experimento se ve que la fuerza decrece por fatiga mostrando la existencia de tres etapas en el tiempo.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El ejercicio se realiza durante 8 minutos en que la persona debe tratar de mantener la mayor fuerza que le sea posible. En la siguiente imagen se muestra como se realiza la fuerza y se indica una curva fuerza vs tiempo a modo de ejemplo:
Ejercicio de fatiga
Los datos resumidos (201 en vez 500050 puntos) se pueden bajar desde
[ muscle_data.xlsx](http://www.gphysics.net/downloads/uach/kinesiologia/muscle_data.xlsx)
muscle_data.xlsx](http://www.gphysics.net/downloads/uach/kinesiologia/muscle_data.xlsx)
B ses de la regresi n
Con la pendiente
La relaci n entre voltaje y fuerza se describe mediante una recta en que la pendiente esta dada por la proporci n entre el rango de fuerzas
Si la relaci n entre voltaje
Si se simplifica esta relaci n a una expresi n en funci n de una pendiente
La constante en particular se puede escribir como:
Los instrumentos de medici n t picamente registran voltajes (mili volts). Por ello es necesario convertir la medici n de voltaje en la magnitud f sica que necesitamos. En este caso dicha magnitud es la fuerza. Si se conoce la fuerza m xima
En muchos casos el instrumento no tiene un offset, o sea la fuerza nula
Definici n de segmentos
Tiempos de etapas
Si se tienen dos rectas calculadas por regresiones
que coinciden en un punto, o sea en
se tiene que
o sea que
En caso de que las fuerzas var an en forma lineal de un valor
Finalmente se puede estimar con el modelo del musculo la secci n.
Con los par metros microsc picos de la estructura del m sculo se puede estimar la potencia para las fuerzas m ximas de cada fase y la energ a consumida en cada una de estas.
La fuerza m xima se logra cuando el m ximo numero de cabezas de mol culas est n activas. Esto es cuando todas las fibras, microfibrillas, miofilamentos y sus respectivas cabezas de mol culas est n activas.
Por ello la fuerza m xima se obtiene multiplicando el numero de fibras
Para calcular la energ a que gasta el musculo debemos conocer por un lado la energ a que consume cada cabeza de mol cula y por otro lado el numero de estas que esta activa.
La energ a depende el mecanismo en si y se puede definir como
Para estimar el numero debemos recordar que se trata de una serie de sarcomeros en paralelo que se acoplan en largas cadenas de
Finalmente el n mero de ciclos se puede estimar del tiempo total que se esta actuando
De esta forma la energ a consumida por el musculo en un tiempo
La potencia es la energ a por tiempo por lo que
por lo que es
La potencia del musculo es del orden de
ID:(63, 0)