Druyd:Knowledge

In der Flüssigkeitssäule

Storyboard

Im Fall einer Flüssigkeitssäule kann das Bernoulli-Gesetz zusammen mit dem hydrostatischen Druckterm angewendet werden. Es ist jedoch wichtig zu beachten, dass bei Nichtberücksichtigung der Viskosität des Fluids die Reduzierung des Niveaus gleichmäßig erfolgt. In diesem Zusammenhang kann es mit der Kontinuitätsgleichung modelliert werden, um die Abwärtsgeschwindigkeit des Zylinders zu bestimmen.Für eine Flüssigkeitssäule mit einem Auslass am Boden zeigt das Verhalten Ähnlichkeiten mit dem, was mit dem Bernoulli-Prinzip geschätzt wird. Unterschiede ergeben sich durch die Bildung kleiner Wirbel am Auslass, die effektiv den Auslassbereich verringern und den Fluss behindern. Der Fluss einer Flüssigkeit mit geringer Viskosität kann jedoch in der Zone ohne Wirbel mit dem Bernoulli-Prinzip modelliert werden.

>Modell

ID:(1427, 0)

Mechanismen

Konzept

ID:(15487, 0)

Statischer und dynamischer Druck

Beschreibung

Wenn vier Säulen mit unterschiedlichen Querschnitten miteinander verbunden sind, nimmt die Flüssigkeit in allen Säulen das gleiche Niveau an. Wenn der verbindende Kanal geöffnet wird, beginnt die Flüssigkeit in Richtung der Öffnung zu fließen, wo der Druck dem Umgebungsdruck entspricht. In der ersten Säule ist der Druck gleich dem Druck der Wassersäule plus dem atmosphärischen Druck, daher ist die Differenz zum Druck am Ausgang der Druck der ersten Säule. Die Flüssigkeit beginnt an Geschwindigkeit zu gewinnen, während der dynamische Druck abnimmt, was sich in den immer kleiner werdenden Säulen zeigt.

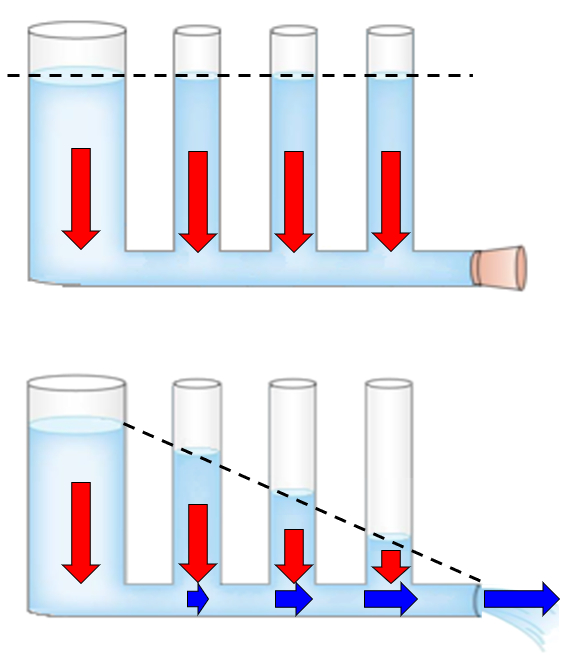
ID:(11092, 0)

Experiment zum entleeren von Säulen

Beschreibung

Dies bedeutet, dass sich mit dem Abnehmen der Säule und der Verringerung der Höhe $h$ auch die Geschwindigkeit $v$ proportional verringert.

Die Schlüsselparameter sind:• Innen-Durchmesser des Gefäßes: 93 mm• Innen-Durchmesser des Evakuierungskanals: 3 mm• Länge des Evakuierungskanals: 18 mmDiese Parameter sind wichtig, um den Prozess des Säulenentleerens zu verstehen und zu analysieren, sowie wie sich die Austrittsgeschwindigkeit mit der Höhe ändert.

ID:(9870, 0)

Modell

Konzept

ID:(15490, 0)

In der Flüssigkeitssäule

Modell

Im Fall einer Flüssigkeitssäule kann das Bernoulli-Gesetz zusammen mit dem hydrostatischen Druckterm angewendet werden. Es ist jedoch wichtig zu beachten, dass bei Nichtberücksichtigung der Viskosität des Fluids die Reduzierung des Niveaus gleichmäßig erfolgt. In diesem Zusammenhang kann es mit der Kontinuitätsgleichung modelliert werden, um die Abwärtsgeschwindigkeit des Zylinders zu bestimmen. Für eine Flüssigkeitssäule mit einem Auslass am Boden zeigt das Verhalten Ähnlichkeiten mit dem, was mit dem Bernoulli-Prinzip geschätzt wird. Unterschiede ergeben sich durch die Bildung kleiner Wirbel am Auslass, die effektiv den Auslassbereich verringern und den Fluss behindern. Der Fluss einer Flüssigkeit mit geringer Viskosität kann jedoch in der Zone ohne Wirbel mit dem Bernoulli-Prinzip modelliert werden.

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$\Delta t$

Abgelaufene Zeit

$S_1$

S_1

Abschnitt in Punkt 1

m^2

$S_2$

S_2

Abschnitt in Punkt 2

m^2

$h_0$

h_0

Anfangshöhe der Flüssigkeitssäule

$\tau_b$

tau_b

Charakteristische Zeitsäule mit Bernoulli

$\rho$

rho

Dichte

kg/m^3

$\Delta p_s$

Dp_s

Druckunterschied

$j_s$

j_s

Flussdichte

m/s

$j_{s1}$

j_s1

Flussdichte 1

m/s

$j_{s2}$

j_s2

Flussdichte 2

m/s

$\rho_w$

rho_w

Flüssigkeitsdichte

kg/m^3

$\Delta h$

Höhe der Flüssigkeitssäule

$h$

Höhe der Säule

$S$

Oberfläche einer Scheibe

m^2

$S$

Rohr Sektion

m^2

$\Delta s$

Rohrelement

$R$

Rohrradius

$r$

Scheibenradius

$v_s$

v_s

Strömungsgeschwindigkeit

m/s

$\Delta p$

Variación de la Presión

$\Delta V$

Volumenelement

m^3

$J_V$

J_V

Volumenstrom

m^3/s

$t$

Zeit

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$\Delta V = S \Delta s$

DV = S * Ds

(ID 3469)

$S = \pi r ^2$

S = pi * r ^2

(ID 3804)

$\Delta p = \rho_w g \Delta h$

Dp = rho_w * g * Dh

Wenn zwischen zwei Punkten die Druckunterschied ( $\Delta p$ ) existiert, wie durch die Gleichung bestimmt:

$dp = p - p_0$

k nnen wir die Druck der Wassersäule ( $p$ ) verwenden, definiert als:

$p_t = p_0 + \rho_w g h$

Dies ergibt:

$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$

Da die Höhendifferenz ( $\Delta h$ ) wie folgt definiert ist:

$\Delta h = h_2 - h_1$

kann die Druckunterschied ( $\Delta p$ ) wie folgt ausgedr ckt werden:

$\Delta p = \rho_w g \Delta h$

(ID 4345)

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

J_V = DV / Dt

(ID 4347)

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

j_s = Ds / Dt

(ID 4348)

$S_1 j_{s1} = S_2 j_{s2}$

S_1 * j_s1 = S_2 * j_s2

(ID 4350)

$S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$

S*DIFF(h,t,1) = pi * R ^2*sqrt(2* g * h )

Mit Hilfe der Bernoulli-Gleichung k nnen wir den Fall einer Wassers ule analysieren, die einen Druckunterschied erzeugt:

$\Delta p = \rho_w g \Delta h$

und einen Geschwindigkeitsfluss $v$ durch ein Rohr verursacht, gem :

$\Delta p = - \rho \bar{v} \Delta v$

Daher k nnen wir die Geschwindigkeit wie folgt sch tzen:

$v = \sqrt{2 g h}$

Diese Geschwindigkeit, durch einen Rohrabchnitt mit Radius $R$ , f hrt zu einem Fluss:

$J = \pi R^2 v$

Wenn die S ule einen Querschnittsbereich $S$ hat und ihre H he im Vergleich zur Variation der H he $h$ im Laufe der Zeit $t$ abnimmt, k nnen wir das Kontinuit tsgesetz anwenden, das besagt:

$S_1 j_{s1} = S_2 j_{s2}$

Daher ist die Gleichung, die diese Situation beschreibt:

$S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$

(ID 9882)

$\tau_b = \displaystyle\frac{S}{\pi R^2}\sqrt{\displaystyle\frac{h_0}{g}}$

tau_b = (S /( pi * R ^2))*sqrt(h_0/g)

(ID 14523)

$h = h_0\left(1-\displaystyle\frac{t}{\tau_b}\right)^2$

h = h_0 *(1-t/tau_b)^2

Wenn in der Gleichung

$S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$

die Konstanten durch

$\tau_b = \displaystyle\frac{S}{\pi R^2}\sqrt{\displaystyle\frac{h_0}{g}}$

ersetzt werden, erhalten wir die lineare Differentialgleichung erster Ordnung

$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_b} \sqrt{h_0 h}$

deren L sung lautet

$h = h_0\left(1-\displaystyle\frac{t}{\tau_b}\right)^2$

(ID 14524)

$v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$

v_s = sqrt(2* Dp_s / rho )

In diesem Fall kann angenommen werden, dass die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ( $v_2$ ) eine Nullgeschwindigkeit darstellt und die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ( $v_1$ ) entspricht die Strömungsgeschwindigkeit ( $v_s$ ). Daher gilt f r die Geschwindigkeitsunterschied zwischen Oberflächen ( $\Delta v$ ) folgendes:

$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$

und f r die Durchschnittsgeschwindigkeit ( $\bar{v}$ ) wird berechnet:

$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$

Folglich ergibt sich mit die Variación de la Presión ( $\Delta p$ ), das gleich die Druckunterschied ( $\Delta p_s$ ) ist, folgendes:

$\Delta p = - \rho \bar{v} \Delta v$

was zu folgendem f hrt:

$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$

was zu:

$v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$

f hrt.

(ID 15710)

$J_V = S j_s$

J_V = S * j_s

Der Volume ( $V$ ) f r ein Rohr mit konstanter die Rohr Sektion ( $S$ ) und eine Position ( $s$ ) ist

$V = h S$

Wenn die Rohr Sektion ( $S$ ) konstant ist, wird die zeitliche Ableitung sein

$\displaystyle\frac{dV}{dt} = S\displaystyle\frac{ds}{dt}$

somit, mit der Volumenstrom ( $J_V$ ) definiert durch

$J_V =\displaystyle\frac{ dV }{ dt }$

und mit die Flussdichte ( $j_s$ ) assoziiert mit die Position ( $s$ ) durch

$j_s =\displaystyle\frac{ ds }{ dt }$

folgt, dass

$J_V = S j_s$

(ID 15716)

Beispiele

Mechanismen

(ID 15487)

Austrittsgeschwindigkeit der Fl ssigkeitss ule

Wenn man eine Höhe der Säule ( $h$ ) Fl ssigkeit mit die Flüssigkeitsdichte ( $\rho_w$ ) unter dem Einfluss der Schwerkraft hat, wird mit die Gravitationsbeschleunigung ( $g$ ) eine die Variación de la Presión ( $\Delta p$ ) gem folgender Gleichung erzeugt:

$\Delta p = \rho_w g \Delta h$

Diese die Variación de la Presión ( $\Delta p$ ) f hrt durch das Auslassrohr mit der Rohrlänge ( $\Delta L$ ), der Rohrradius ( $R$ ) und die Viskosität ( $\eta$ ) zu einem Fluss von ein Volumenstrom 1 ( $J_{V1}$ ) gem dem Hagen-Poiseuille-Gesetz:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Da diese Gleichung die Abschnitt in Punkt 2 ( $S_2$ ) enth lt, kann die Flussdichte 2 ( $j_{s2}$ ) berechnet werden mittels:

$j_s = \displaystyle\frac{ J_V }{ S }$

Damit erh lt man:

$j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h$

was einer mittleren Geschwindigkeit entspricht.

Um das System zu modellieren, sind die Schl sseldaten:• Innendurchmesser des Beh lters: 93 mm• Innendurchmesser des Abflusskanals: 3,2 mm• L nge des Abflusskanals: 18 mmDie anf ngliche Fl ssigkeitsh he betr gt 25 cm.

(ID 11092)

Experiment zum Entleeren von S ulen: Model mit Bernoulli

Betrachten wir das System eines zylindrischen Eimers mit einem Abflussloch. Wenn der Stopfen entfernt wird, beginnt das Wasser aufgrund des vorhandenen Drucks zu flie en. Gem dem Bernoulli-Prinzip ist die Geschwindigkeit im Inneren des Eimers ( $v\sim 0$ ) null, und wir haben:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$

w hrend au erhalb des Eimers ( $h=0$ ) nur die kinetische Komponente vorhanden ist:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$

Da beide Ausdr cke gleich sind, haben wir:

$\displaystyle\frac{1}{2}\rho v^2=\rho g h$

was zur Geschwindigkeit f hrt:

$v=\sqrt{2 g h}$

Um den Versuch mit der Theorie zu vergleichen, k nnen wir diesen Ausdruck verwenden, um mit:

$S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$

die Reichweite zu berechnen, die der Strahl haben sollte. Wenn wir dies grafisch darstellen, beobachten wir:

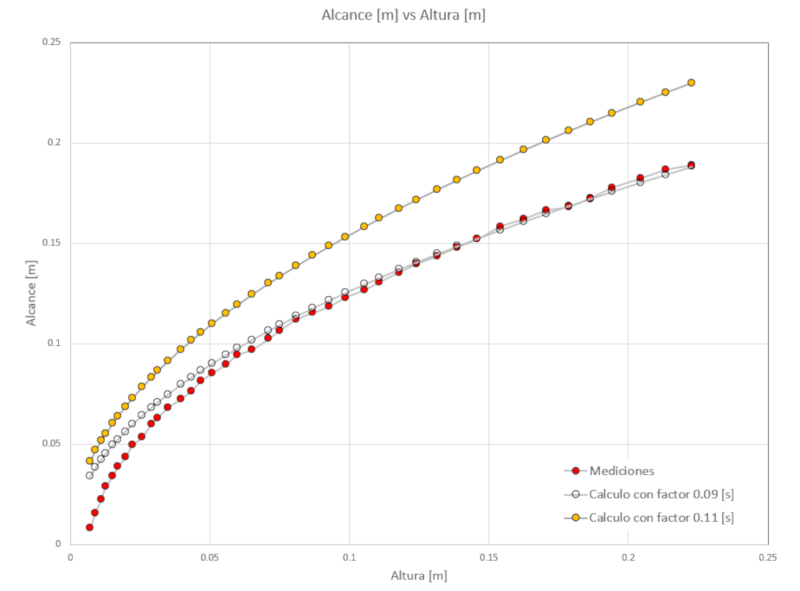
wo:• die roten Punkte den experimentellen Messungen entsprechen,• die blauen Punkte der berechneten Reichweite unter Verwendung eines Faktors von 0,11 entsprechen,• die transparenten Punkte der berechneten Reichweite unter Verwendung eines Faktors von 0,09 entsprechen.Daher k nnen wir folgern, dass das Bernoulli-Modell die Geschwindigkeit, mit der der Eimer sich entleert, bersch tzt. Dies liegt daran, dass in der N he des Abflusslochs die Auswirkungen der Viskosit t nicht vernachl ssigbar sind und die Geschwindigkeit daher geringer ist.

(ID 11063)

Experiment zum Entleeren von S ulen: H he und Reichweite

Wenn das Tracker-Programm verwendet wird, k nnen die H he des Meniskus der S ule und die Reichweite des Strahls gemessen werden. Das Verh ltnis zwischen beiden wird im folgenden Diagramm dargestellt:

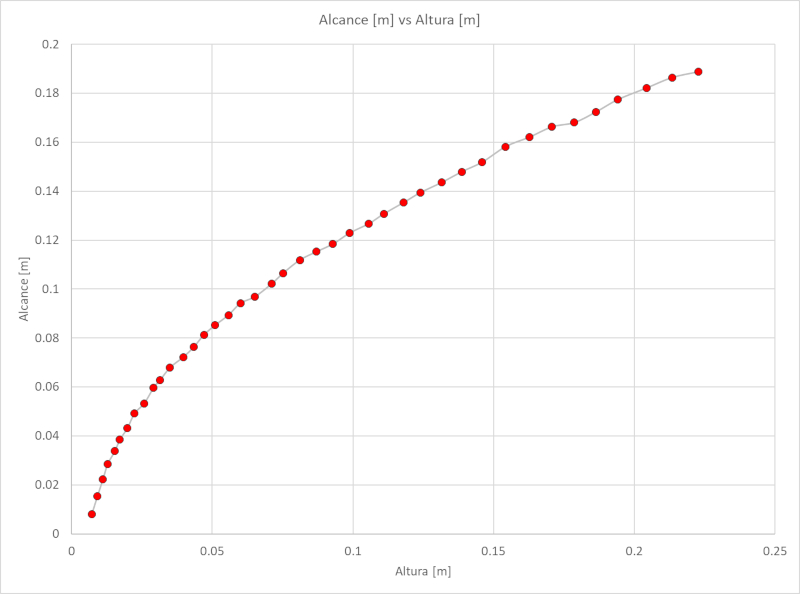
Reichweite [m] vs H he [m]

Die aufgezeichneten Daten, die als Excel-Tabelle unter folgendem Link heruntergeladen werden k nnen Excel-Tabelle, lauten wie folgt:

Zeit [s]	H he [m]	Weite [m]
0	2.23E-01	1.89E-01
4	2.14E-01	1.86E-01
8	2.04E-01	1.82E-01
12	1.94E-01	1.77E-01
16	1.86E-01	1.72E-01
20	1.79E-01	1.68E-01
24	1.71E-01	1.66E-01
28	1.63E-01	1.62E-01
32	1.54E-01	1.58E-01
36	1.46E-01	1.52E-01
40	1.39E-01	1.48E-01
44	1.32E-01	1.44E-01
48	1.24E-01	1.39E-01
52	1.18E-01	1.35E-01
56	1.11E-01	1.31E-01
60	1.06E-01	1.27E-01
64	9.88E-02	1.23E-01
68	9.29E-02	1.18E-01
72	8.70E-02	1.15E-01
76	8.11E-02	1.12E-01
80	7.52E-02	1.06E-01
84	7.12E-02	1.02E-01
88	6.51E-02	9.69E-02
92	6.00E-02	9.42E-02
96	5.58E-02	8.94E-02
100	5.09E-02	8.52E-02
104	4.70E-02	8.13E-02
108	4.34E-02	7.63E-02
112	3.97E-02	7.22E-02
116	3.49E-02	6.79E-02
120	3.15E-02	6.28E-02
124	2.91E-02	5.96E-02
128	2.58E-02	5.33E-02
132	2.23E-02	4.92E-02
136	1.98E-02	4.31E-02
140	1.71E-02	3.85E-02
144	1.54E-02	3.38E-02
148	1.28E-02	2.85E-02
152	1.11E-02	2.23E-02
156	9.17E-03	1.54E-02
160	7.15E-03	7.95E-03

Hinweis: E ist wissenschaftliche Notation (zB. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)

(ID 11062)

Modell

(ID 15490)

ID:(1427, 0)