Druyd:Knowledge

Ley de Boyle-Mariotte

Storyboard

La ley de Boyle-Mariotte establece que el producto de la presión ($p$) y el volumen ($V$) de un gas se mantiene constante cuando la temperatura absoluta y la cantidad de moles no varían.

Esto significa que la presión ($p$) varía inversamente proporcional a el volumen ($V$).

>Modelo

ID:(1472, 0)

Mecanismos

Concepto

La ley de Boyle-Mariotte, también conocida simplemente como la ley de Boyle, describe la relación inversa entre la presión y el volumen de un gas a temperatura constante. Establece que para una cantidad fija de gas, cuando la temperatura se mantiene constante, la presión del gas aumenta a medida que el volumen disminuye, y viceversa. Esto significa que si comprimes un gas reduciendo su volumen, su presión aumentará proporcionalmente, y si expandes el volumen, la presión disminuirá proporcionalmente. Esta relación es fundamental para entender el comportamiento de los gases y se expresa matemáticamente por el producto de la presión y el volumen siendo una constante para una cantidad de gas dada a temperatura constante.

ID:(15254, 0)

Variación del volumen y presión

Concepto

La presión ($p$) se genera al chocar las partículas del gas con la superficie del contenedor del gas. Al ser la temperatura absoluta ($T$) constante, la energía de las partículas no varían y los golpes de estas con las superficies del contenedor del gas no variarán en el impulso transferido. Sin embargo, el número de impactos depende del número de partículas próximas a la superficie que, a su vez, es proporcional a la concentración de particulas ($c_n$) del gas.

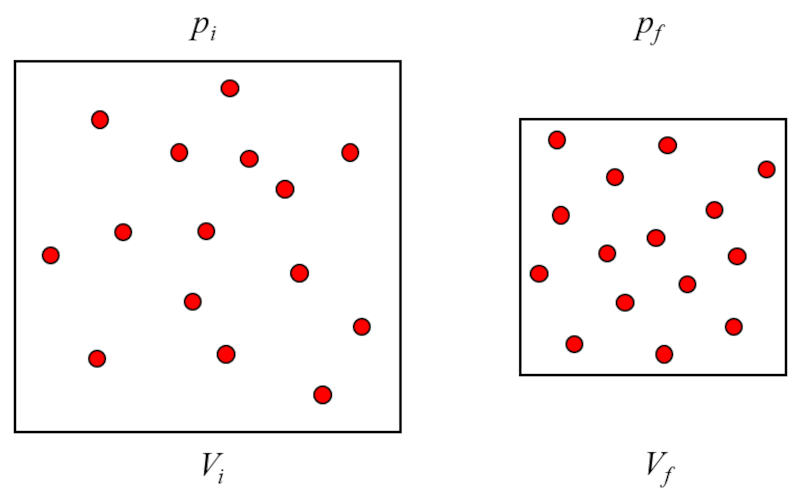
Por otro lado, la densidad es inversamente proporcional a el volumen ($V$), lo que nos lleva a la siguiente relación:

$p \propto c_n \propto \displaystyle\frac{1}{V}$

ID:(9602, 0)

Relación volumen y presión

Descripción

En un gas, si se mantienen la temperatura absoluta ($T$) y el número de partículas ($N$) constantes, se observa que el volumen ($V$) y la presión ($p$) varían de forma inversamente proporcional. Cada vez que se reduce el volumen ($V$), se observa que la presión ($p$) aumenta y viceversa,

$p \propto \displaystyle\frac{1}{V}$

como se ilustra en el siguiente gráfico:

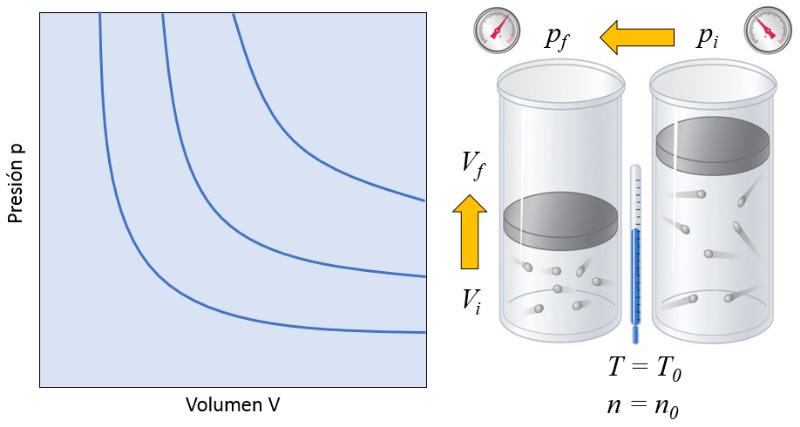
La relación entre el número de partículas ($N$) y la temperatura absoluta ($T$) es que su producto es igual a una constante de la ley de Boyle ($C_b$), lo que corresponde a la ley de Boyle [1], en honor a su descubridor Robert Boyle:

$ p V = C_b $

Algunas veces se habla de la ley Boyle-Mariotte recordando al físico frances Edme Mariotte que descubrio en 1676 la misma ley en forma independiente. [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Nuevos experimentos físico-mecánicos, tocando el resorte del aire y sus efectos), Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).

ID:(9531, 0)

Robert Boyle

Descripción

Robert Boyle fue un científico irlandés nacido en 1627. Es considerado uno de los fundadores de la química moderna y es conocido por sus contribuciones en el campo del comportamiento de los gases. La relación entre Robert Boyle y la Ley de Boyle se debe a que él formuló dicha ley en el siglo XVII. La Ley de Boyle establece que, a temperatura constante, el volumen de un gas es inversamente proporcional a su presión. Boyle realizó experimentos que demostraron esta relación y sentaron las bases para comprender el comportamiento de los gases.

Robert Boyle (1627-1691)

ID:(1657, 0)

Cambio de estado de un gas ideal según la ley de Boyle

Concepto

La ley de Boyle establece que, con la temperatura absoluta ($T$) constante, se cumple que el producto de la presión ($p$) y el volumen ($V$) es igual a la constante de la ley de Boyle ($C_b$):

$ p V = C_b $

Esto significa que si un gas pasa de un estado inicial (la presión en estado inicial ($p_i$) y el volumen en estado i ($V_i$)) a un estado final (la presión en estado final ($p_f$) y el volumen en estado f ($V_f$)), manteniendo la temperatura absoluta ($T$) constante, debe siempre cumplir la ley de Boyle:

$p_i V_i = C_b = p_f V_f$

Por lo tanto, se tiene que:

$ p_i V_i = p_f V_f $

ID:(15688, 0)

Equivalente a la ley de Boyle para densidades

Concepto

Si en un cambio isotérmico en el que no varía el contenido se cumple que la presión en estado inicial ($p_i$), la presión en estado final ($p_f$), el volumen en estado i ($V_i$), y el volumen en estado f ($V_f$) están relacionados por:

$ p_i V_i = p_f V_f $

Entonces, se puede introducir la densidad ($\rho$), que con la masa ($M$) y el volumen ($V$) cumple:

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Lo que nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

ID:(15687, 0)

Modelo

Concepto

ID:(15313, 0)

Ley de Boyle-Mariotte

Modelo

La ley de Boyle-Mariotte establece que el producto de 5224 y 5226 de un gas se mantiene constante cuando la temperatura absoluta y la cantidad de moles no varían. Esto significa que 5224 varía inversamente proporcional a 5226.

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$C_b$

C_b

Constante de la ley de Boyle

$\rho_f$

rho_f

Densidad en estado f

kg/m^3

$\rho_i$

rho_i

Densidad en estado i

kg/m^3

$M$

Masa

$p_f$

p_f

Presión en estado final

$p_i$

p_i

Presión en estado inicial

$V_f$

V_f

Volumen en estado f

m^3

$V_i$

V_i

Volumen en estado i

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ p V = C_b $

p * V = C_b

(ID 582)

$ p V = C_b $

p * V = C_b

(ID 582)

$ p_i V_i = p_f V_f $

p_i * V_i = p_f * V_f

La ley de Boyle establece que, con la temperatura absoluta ($T$) constante, se cumple que el producto de la presión ($p$) y el volumen ($V$) es igual a la constante de la ley de Boyle ($C_b$):

$ p V = C_b $

$p_i V_i = C_b = p_f V_f$

Por lo tanto, se tiene que:

$ p_i V_i = p_f V_f $

(ID 3491)

$ \rho \equiv\displaystyle\frac{ M }{ V }$

rho = M / V

(ID 3704)

$ \rho \equiv\displaystyle\frac{ M }{ V }$

rho = M / V

(ID 3704)

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

p_i / rho_i = p_f / rho_f

Si en un cambio isot rmico en el que no var a el contenido se cumple que la presión en estado inicial ($p_i$), la presión en estado final ($p_f$), el volumen en estado i ($V_i$), y el volumen en estado f ($V_f$) est n relacionados por:

$ p_i V_i = p_f V_f $

Entonces, se puede introducir la densidad ($\rho$), que con la masa ($M$) y el volumen ($V$) cumple:

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Lo que nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

(ID 8834)

Ejemplos

Simulador de gas

La ley de Boyle-Mariotte, tambi n conocida simplemente como la ley de Boyle, describe la relaci n inversa entre la presi n y el volumen de un gas a temperatura constante. Establece que para una cantidad fija de gas, cuando la temperatura se mantiene constante, la presi n del gas aumenta a medida que el volumen disminuye, y viceversa. Esto significa que si comprimes un gas reduciendo su volumen, su presi n aumentar proporcionalmente, y si expandes el volumen, la presi n disminuir proporcionalmente. Esta relaci n es fundamental para entender el comportamiento de los gases y se expresa matem ticamente por el producto de la presi n y el volumen siendo una constante para una cantidad de gas dada a temperatura constante.

(ID 15254)

Variaci n del volumen y presi n

La presión ($p$) se genera al chocar las part culas del gas con la superficie del contenedor del gas. Al ser la temperatura absoluta ($T$) constante, la energ a de las part culas no var an y los golpes de estas con las superficies del contenedor del gas no variar n en el impulso transferido. Sin embargo, el n mero de impactos depende del n mero de part culas pr ximas a la superficie que, a su vez, es proporcional a la concentración de particulas ($c_n$) del gas.

Por otro lado, la densidad es inversamente proporcional a el volumen ($V$), lo que nos lleva a la siguiente relaci n:

$p \propto c_n \propto \displaystyle\frac{1}{V}$

(ID 9602)

Relaci n volumen y presi n

En un gas, si se mantienen la temperatura absoluta ($T$) y el número de partículas ($N$) constantes, se observa que el volumen ($V$) y la presión ($p$) var an de forma inversamente proporcional. Cada vez que se reduce el volumen ($V$), se observa que la presión ($p$) aumenta y viceversa,

$p \propto \displaystyle\frac{1}{V}$

como se ilustra en el siguiente gr fico:

La relaci n entre el número de partículas ($N$) y la temperatura absoluta ($T$) es que su producto es igual a una constante de la ley de Boyle ($C_b$), lo que corresponde a la ley de Boyle [1], en honor a su descubridor Robert Boyle:

$ p V = C_b $

Algunas veces se habla de la ley Boyle-Mariotte recordando al f sico frances Edme Mariotte que descubrio en 1676 la misma ley en forma independiente. [1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Nuevos experimentos f sico-mec nicos, tocando el resorte del aire y sus efectos), Robert Boyle, Oxford: printed by H. Hall, Printer to the University, for Tho. Robinson (1660).

(ID 9531)

Robert Boyle

Robert Boyle fue un cient fico irland s nacido en 1627. Es considerado uno de los fundadores de la qu mica moderna y es conocido por sus contribuciones en el campo del comportamiento de los gases. La relaci n entre Robert Boyle y la Ley de Boyle se debe a que l formul dicha ley en el siglo XVII. La Ley de Boyle establece que, a temperatura constante, el volumen de un gas es inversamente proporcional a su presi n. Boyle realiz experimentos que demostraron esta relaci n y sentaron las bases para comprender el comportamiento de los gases.

Robert Boyle (1627-1691)

(ID 1657)

Cambio de estado de un gas ideal seg n la ley de Boyle

La ley de Boyle establece que, con la temperatura absoluta ($T$) constante, se cumple que el producto de la presión ($p$) y el volumen ($V$) es igual a la constante de la ley de Boyle ($C_b$):

$ p V = C_b $

$p_i V_i = C_b = p_f V_f$

Por lo tanto, se tiene que:

$ p_i V_i = p_f V_f $

(ID 15688)

Equivalente a la ley de Boyle para densidades

$ p_i V_i = p_f V_f $

Entonces, se puede introducir la densidad ($\rho$), que con la masa ($M$) y el volumen ($V$) cumple:

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Lo que nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

(ID 15687)

Modelo

(ID 15313)

ID:(1472, 0)