Usuario:
Transferencia de calor
Storyboard 
El calor se conduce dentro de un medio hasta la interfaz con otro medio. Entre ambos, el calor se transfiere en función de la diferencia de temperatura entre los medios, la superficie de contacto y una constante de transferencia térmica. Cuando uno de los medios es un gas (por ejemplo, aire) o un líquido (por ejemplo, agua), la constante de transferencia térmica depende de la estructura de la interfaz y de la velocidad de desplazamiento del medio gaseoso o líquido.
ID:(776, 0)
Dependencia de la transmisión de calor de la geometría al conductor
Imagen
El principal impulsor de la transferencia de calor desde un medio a un conductor es la diferencia de temperatura. Cuando en el medio la temperatura en el interior ($T_i$), las partículas poseen más energía y al chocar con las del conductor a una temperatura en la superficie interior ($T_{is}$), tienden a aumentar la energía de este último. Esta interacción se puede representar de la siguiente manera:
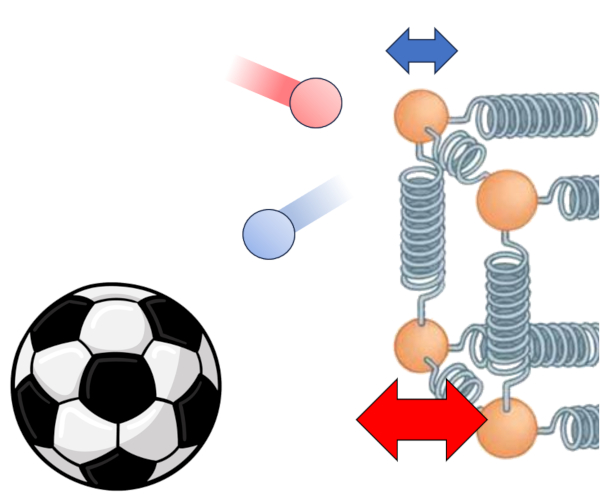
Además de la temperatura en sí, el flujo de calor depende de la diferencia de temperatura en interfaz interna ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Otro factor clave es el número de átomos a los que se les puede aumentar la amplitud de la oscilación, lo cual depende de la sección ($S$). Por último, debemos considerar las propiedades de la superficie, que se describen mediante el coeficiente de transmisión interno ($\alpha_i$), que corresponde a la relación entre el calor transmitido, la superficie, la diferencia de temperatura y el tiempo transcurrido:
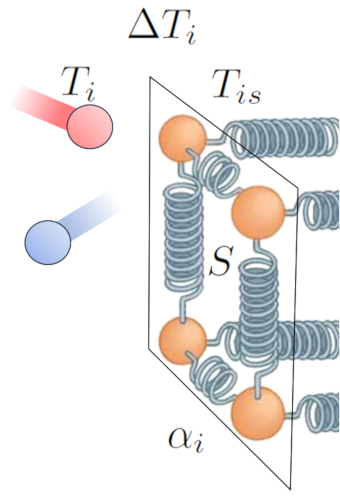
ID:(15237, 0)
Calculo de la transmisión de calor al conductor
Nota
De esta forma, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en interfaz interna ($\Delta T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
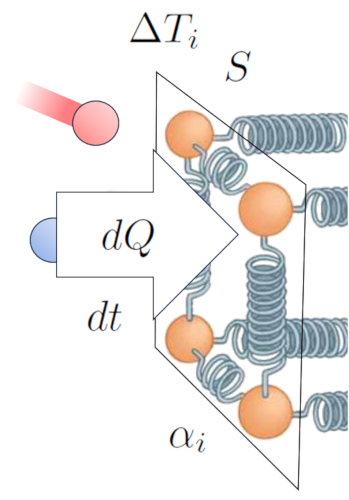
Esta expresión puede formularse matemáticamente de la siguiente manera:
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Dependencia de la transmisión de calor de la geometría desde el conductor
Cita
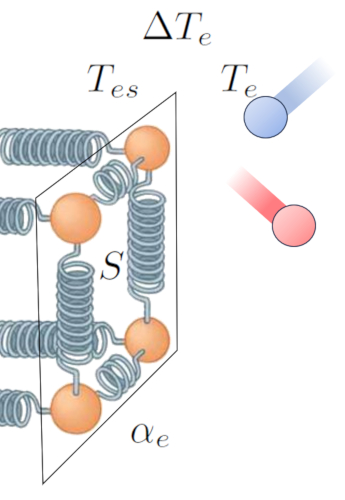
El principal impulsor de la transferencia de calor desde un conductor hacia un medio es la diferencia de temperatura. Cuando la temperatura en la superficie exterior ($T_{es}$), las partículas tienen más energía y oscilan con una amplitud mayor al interactuar con los átomos y moléculas del medio a una temperatura en el exterior ($T_e$). Esto tiende a aumentar la energía de estos últimos. Esta interacción se puede representar de la siguiente manera:
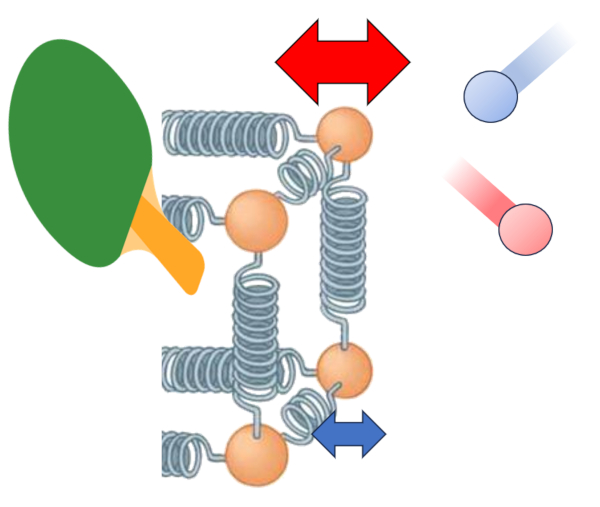
Además de la temperatura, el flujo de calor depende de la diferencia de temperatura en la interfaz externa ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Otro factor clave es el número de átomos que pueden tener aumentada su amplitud de oscilación, lo cual depende de la sección ($S$). Finalmente, debemos considerar las propiedades superficiales, representadas por el coeficiente de transmisión externo ($\alpha_e$), que corresponde a la relación entre el calor transmitido, el área superficial, la diferencia de temperatura y el tiempo transcurrido:
ID:(15239, 0)
Transmisión de calor desde el conductor
Ejercicio
De esta manera, establecemos una relación que nos permite calcular la tasa de flujo de calor ($q$) en función de la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y el coeficiente de transmisión externo ($\alpha_e$):
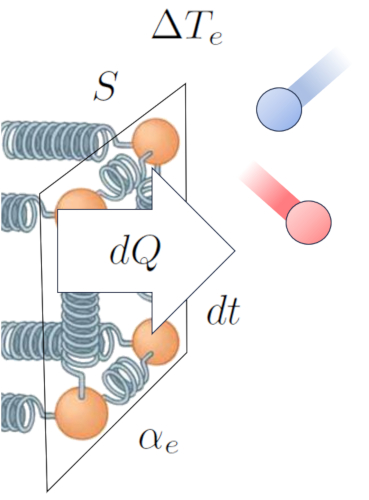
Matemáticamente, esto puede expresarse de la siguiente manera:
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Transmisión de calor desde y hacia el conductor
Ecuación
La primera descripción del modelo de transmisión de calor en la interfaz entre dos medios fue desarrollada por Thomas Graham Balfour [1]. Su teoría postula que la tasa de calor transmitido depende de la diferencia de temperatura y de una constante característica de la interfaz.
Cuando el calor se transfiere al conductor, representado por la tasa de flujo de calor ($q$) junto con el coeficiente de transmisión interno ($\alpha_i$) y la diferencia de temperatura en interfaz interna ($\Delta T_i$), la relación se expresa mediante:
| $ q = \alpha_i \Delta T_i $ |
En el caso de que el calor se transfiera desde el conductor, identificado por la tasa de flujo de calor ($q$) con el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$), la relación se especifica como:
| $ q = \alpha_e \Delta T_e $ |
[1] "The Theory of Heat" (La teoría del calor), Thomas Graham Balfour, 1876.
ID:(15123, 0)
Transporte de calor
Script
El sistema básico incluye una transferencia generada por la diferencia de temperatura ($\Delta T$), que consta de la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$). Por lo tanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Con la tasa de flujo de calor ($q$) siendo el responsable de la transferencia entre el interior y el conductor, mediante el coeficiente de transmisión interno ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
La conducción involucra a la conductividad térmica ($\lambda$) y el largo del conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Y la transferencia del conductor al exterior, con el coeficiente de transmisión externo ($\alpha_e$) se representa por:
| $ q = \alpha_e \Delta T_e $ |
Todo esto está representado gráficamente por:
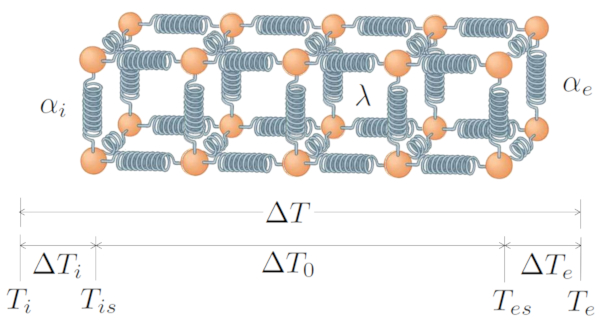
Transferencia de calor
ID:(7723, 0)
Dependencia del coeficiente de transferencia de la velocidad del medio
Variable
Uno de los efectos de la transferencia de calor de un conductor a un medio externo es el calentamiento del medio cercano a la interfaz, creando una zona de interferencia en la transmisión. Esto disminuye la eficiencia de la transferencia y tiende a formar una capa aislante que reduce el flujo de energía.
Sin embargo, este efecto puede modificarse en presencia de viento. El viento puede disipar la capa de átomos y moléculas a alta temperatura, aumentando la eficiencia de la transferencia de calor. Esto indica que el coeficiente de transmisión ($\alpha$) está influenciado por la velocidad del medio ($v_m$) [1,2]:
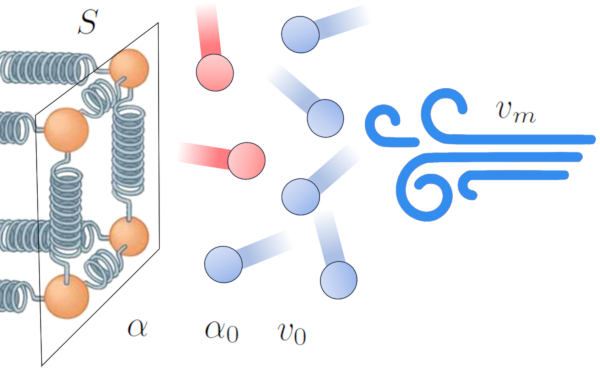
En este contexto, modelamos la relación en función de ERROR:9844,0 y un factor de referencia el velocidad de referencia del medio ($v_0$).
La relación matemática que describe este fenómeno para un gas con el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Y para un líquido con el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Esto demuestra cómo el viento puede afectar significativamente la eficiencia de la transferencia de calor entre un conductor y un medio externo.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" (Sobre el movimiento de fluidos con muy poca fricción), Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge" (La dependencia del coeficiente de transferencia de calor de la longitud del tubo), Wilhelm Nusselt, 1910
ID:(3620, 0)
Transferencia de calor
Storyboard
El calor se conduce dentro de un medio hasta la interfaz con otro medio. Entre ambos, el calor se transfiere en función de la diferencia de temperatura entre los medios, la superficie de contacto y una constante de transferencia térmica. Cuando uno de los medios es un gas (por ejemplo, aire) o un líquido (por ejemplo, agua), la constante de transferencia térmica depende de la estructura de la interfaz y de la velocidad de desplazamiento del medio gaseoso o líquido.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Si se suman la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y se usan las ecuaciones
y
se obtiene
$\Delta T_i + \Delta T_0 + \Delta T_e = T_i - T_e$
que con
resulta
Ejemplos
Considere un volumen con part culas que rebotan contra las paredes con una velocidad que representa su temperatura. Cada vez que estas part culas impactan una red ubicada en el centro, colisionan con los tomos del s lido y los inducen a oscilar. Esta oscilaci n se propaga a trav s del s lido hasta alcanzar el otro extremo, donde las part culas del gas reciben la energ a transferida a trav s de nuevos impactos.
Experimentaci n:
Es posible modificar la velocidad de las part culas en las cajas laterales y observar c mo la energ a es transferida al s lido y, posteriormente, al gas del lado opuesto.
El principal impulsor de la transferencia de calor desde un medio a un conductor es la diferencia de temperatura. Cuando en el medio la temperatura en el interior ($T_i$), las part culas poseen m s energ a y al chocar con las del conductor a una temperatura en la superficie interior ($T_{is}$), tienden a aumentar la energ a de este ltimo. Esta interacci n se puede representar de la siguiente manera:
Adem s de la temperatura en s , el flujo de calor depende de la diferencia de temperatura en interfaz interna ($\Delta T_i$):
Otro factor clave es el n mero de tomos a los que se les puede aumentar la amplitud de la oscilaci n, lo cual depende de la sección ($S$). Por ltimo, debemos considerar las propiedades de la superficie, que se describen mediante el coeficiente de transmisión interno ($\alpha_i$), que corresponde a la relaci n entre el calor transmitido, la superficie, la diferencia de temperatura y el tiempo transcurrido:
De esta forma, establecemos una relaci n que nos permite calcular la tasa de flujo de calor ($q$) en funci n de la diferencia de temperatura en interfaz interna ($\Delta T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
Esta expresi n puede formularse matem ticamente de la siguiente manera:
El principal impulsor de la transferencia de calor desde un conductor hacia un medio es la diferencia de temperatura. Cuando la temperatura en la superficie exterior ($T_{es}$), las part culas tienen m s energ a y oscilan con una amplitud mayor al interactuar con los tomos y mol culas del medio a una temperatura en el exterior ($T_e$). Esto tiende a aumentar la energ a de estos ltimos. Esta interacci n se puede representar de la siguiente manera:
Adem s de la temperatura, el flujo de calor depende de la diferencia de temperatura en la interfaz externa ($\Delta T_e$).
Otro factor clave es el n mero de tomos que pueden tener aumentada su amplitud de oscilaci n, lo cual depende de la sección ($S$). Finalmente, debemos considerar las propiedades superficiales, representadas por el coeficiente de transmisión externo ($\alpha_e$), que corresponde a la relaci n entre el calor transmitido, el rea superficial, la diferencia de temperatura y el tiempo transcurrido:
De esta manera, establecemos una relaci n que nos permite calcular la tasa de flujo de calor ($q$) en funci n de la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y el coeficiente de transmisión externo ($\alpha_e$):
Matem ticamente, esto puede expresarse de la siguiente manera:
La primera descripci n del modelo de transmisi n de calor en la interfaz entre dos medios fue desarrollada por Thomas Graham Balfour [1]. Su teor a postula que la tasa de calor transmitido depende de la diferencia de temperatura y de una constante caracter stica de la interfaz.
Cuando el calor se transfiere al conductor, representado por la tasa de flujo de calor ($q$) junto con el coeficiente de transmisión interno ($\alpha_i$) y la diferencia de temperatura en interfaz interna ($\Delta T_i$), la relaci n se expresa mediante:
En el caso de que el calor se transfiera desde el conductor, identificado por la tasa de flujo de calor ($q$) con el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$), la relaci n se especifica como:
[1] "The Theory of Heat" (La teor a del calor), Thomas Graham Balfour, 1876.
El sistema b sico incluye una transferencia generada por la diferencia de temperatura ($\Delta T$), que consta de la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$). Por lo tanto:
Con la tasa de flujo de calor ($q$) siendo el responsable de la transferencia entre el interior y el conductor, mediante el coeficiente de transmisión interno ($\alpha_i$):
La conducci n involucra a la conductividad térmica ($\lambda$) y el largo del conductor ($L$):
Y la transferencia del conductor al exterior, con el coeficiente de transmisión externo ($\alpha_e$) se representa por:
Todo esto est representado gr ficamente por:
Uno de los efectos de la transferencia de calor de un conductor a un medio externo es el calentamiento del medio cercano a la interfaz, creando una zona de interferencia en la transmisi n. Esto disminuye la eficiencia de la transferencia y tiende a formar una capa aislante que reduce el flujo de energ a.
Sin embargo, este efecto puede modificarse en presencia de viento. El viento puede disipar la capa de tomos y mol culas a alta temperatura, aumentando la eficiencia de la transferencia de calor. Esto indica que el coeficiente de transmisión ($\alpha$) est influenciado por la velocidad del medio ($v_m$) [1,2]:
En este contexto, modelamos la relaci n en funci n de ERROR:9844,0 y un factor de referencia el velocidad de referencia del medio ($v_0$).
La relaci n matem tica que describe este fen meno para un gas con el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es:
Y para un l quido con el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$), la velocidad del medio ($v_m$), el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$):
Esto demuestra c mo el viento puede afectar significativamente la eficiencia de la transferencia de calor entre un conductor y un medio externo.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre el movimiento de fluidos con muy poca fricci n), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (La dependencia del coeficiente de transferencia de calor de la longitud del tubo), Wilhelm Nusselt, 1910
La diferencia de temperatura en interfaz interna ($\Delta T_i$) se calcula restando la temperatura en la superficie interior ($T_{is}$) de la temperatura en el interior ($T_i$):
La diferencia de temperatura en la interfaz externa ($\Delta T_e$) se calcula restando la temperatura en la superficie exterior ($T_{es}$) de la temperatura en el exterior ($T_e$):
En el caso de un s lido, y de manera similar para un l quido, podemos describir el sistema como una estructura de tomos unidos por algo que se comporta como un resorte. Cuando ambos extremos tienen valores de temperatura de una diferencia de temperatura en el conductor ($\Delta T_0$), siendo la temperatura en la superficie interior ($T_{is}$) y la temperatura en la superficie exterior ($T_{es}$):
En el proceso de transporte de calor, la temperatura disminuye gradualmente desde el sistema con mayor temperatura (interno) al de menor temperatura (externo). En este proceso, primero desciende desde la temperatura media interna hasta llegar a la diferencia de temperatura en interfaz interna ($\Delta T_i$), luego a la diferencia de temperatura en el conductor ($\Delta T_0$) y finalmente a la diferencia de temperatura en la interfaz externa ($\Delta T_e$). La suma de estas tres variaciones equivale a la ca da total, es decir, la diferencia de temperatura ($\Delta T$), como se muestra a continuaci n:
El la tasa de flujo de calor ($q$) se define en funci n de la calor transportado ($dQ$) que pasa por la sección ($S$) en la variación de tiempo ($dt$):
De esta forma, establecemos una relaci n que nos permite calcular la tasa de flujo de calor ($q$) en funci n de la diferencia de temperatura en interfaz interna ($\Delta T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
De esta manera, establecemos una relaci n que nos permite calcular la tasa de flujo de calor ($q$) en funci n de la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y el coeficiente de transmisión externo ($\alpha_e$):
El flujo de calor ($q$) es una funci n de la conductividad térmica ($\lambda$), el largo del conductor ($L$) y la diferencia de temperatura en el conductor ($\Delta T_0$):
Si un medio se desplaza con una constante de el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$) y la velocidad del medio ($v_m$) es igual a
donde el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$) es la velocidad de referencia.
La constante de transferencia t rmica del material para el caso de un l quido en reposo es igual a $340 J/m^2sK$, mientras que la velocidad de referencia es de $0.0278 m/s$.
Si un medio se desplaza con una constante de el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$) y la velocidad del medio ($v_m$) es igual a
donde el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es la velocidad de referencia.
La constante de transferencia t rmica del material en el caso de un gas en reposo es de $5.6 J/m^2sK$, mientras que la velocidad de referencia es de $1.41 m/s$
ID:(776, 0)