Utilisateur:
Force et couple
Description 
Comme nous l'avons vu, le moment de force joue un rôle analogue à la force dans le cas de la rotation :
$F\longleftrightarrow T$
Pour établir les équations de mouvement, nous pouvons rappeler comment la force a été définie en termes de quantité de mouvement :
$F=\displaystyle\frac{\Delta p}{\Delta t}$
et comment le moment de force a été défini :
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Nous pouvons établir une relation entre les deux pour décrire la génération de moment de force en fonction de la force :
Par conséquent, nous devons d'abord définir ce qui équivaut à la Quantité de mouvement dans le contexte de la rotation.
ID:(325, 0)
Notion de centre de masse (CM)
Image
Si l'on considère la répartition de la masse dans l'espace, il devrait toujours être possible d'identifier un point où la force exercée par la masse d'un côté est égale à la force générée de l'autre côté :
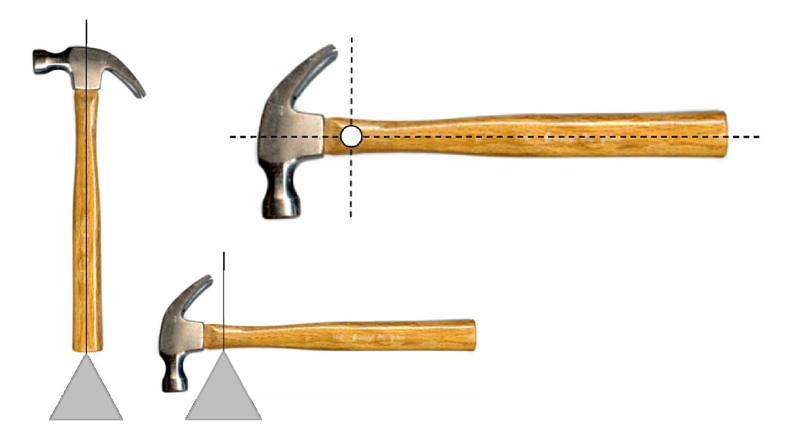
Ce concept implique que, pour n'importe quelle orientation d'un objet, un point d'appui peut être localisé, où l'objet est en équilibre. Chacun de ces points correspond à une ligne verticale. En répétant ce processus avec différentes orientations de l'objet, il devient évident que les lignes verticales se croisent en un point spécifique à l'intérieur de l'objet. Ce point est appelé centre de masse (CM). En essence, le centre de masse est le point unique à l'intérieur de l'objet où, quelle que soit son orientation, l'équilibre est toujours atteint.
ID:(323, 0)
Définition du centre de masse (CM)
Image
On peut définir le centre de masse comme le point où toutes les lignes verticales tracées à travers les points où le système est en équilibre se croisent :
ID:(11603, 0)
Trajectoire d'un corps avec translation et rotation
Image
Tout corps qui se déplace et tourne le fait de manière à ce que :
• son mouvement de translation puisse être décrit comme si toute la masse était concentrée au centre de masse,
• sa rotation s'effectue autour du centre de masse comme s'il n'était pas en translation.
ID:(11604, 0)
Couple, règle de la main droite
Image
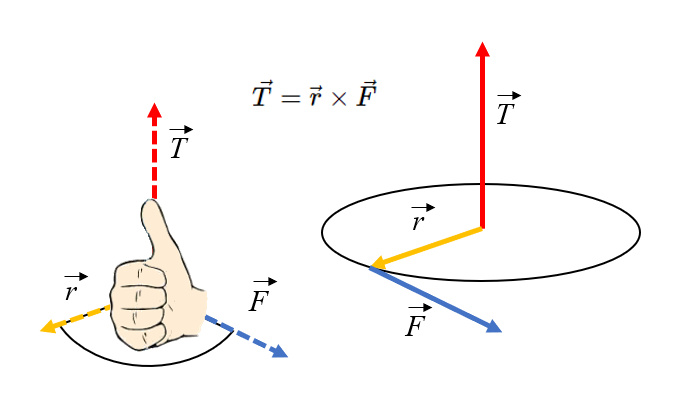
L'orientation du couple peut être déterminée à l'aide de la règle de la main droite : si vous pointez vos doigts dans la direction du rayon et que vous tournez dans le sens de la force,
ID:(11602, 0)
Génération de couple
Modèle
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3241)
Dans le cas d'une balance, une force gravitationnelle agit sur chaque bras, g n rant un couple
| $ T = r F $ |
Si les longueurs des bras sont $d_i$ et les forces sont $F_i$ avec $i=1,2$, la condition d' quilibre exige que la somme des couples soit nulle :
| $\displaystyle\sum_i \vec{T}_i=0$ |
Par cons quent, en consid rant que le signe de chaque couple d pend de la direction dans laquelle il induit une rotation,
$d_1F_1-d_2F_2=0$
ce qui donne comme r sultat
.
(ID 3250)
(ID 4431)
Exemples
Comme nous l'avons vu, le moment de force joue un r le analogue la force dans le cas de la rotation :
$F\longleftrightarrow T$
Pour tablir les quations de mouvement, nous pouvons rappeler comment la force a t d finie en termes de quantit de mouvement :
$F=\displaystyle\frac{\Delta p}{\Delta t}$
et comment le moment de force a t d fini :
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Nous pouvons tablir une relation entre les deux pour d crire la g n ration de moment de force en fonction de la force :
Par cons quent, nous devons d'abord d finir ce qui quivaut la Quantit de mouvement dans le contexte de la rotation.
(ID 325)
Si l'on consid re la r partition de la masse dans l'espace, il devrait toujours tre possible d'identifier un point o la force exerc e par la masse d'un c t est gale la force g n r e de l'autre c t :
Ce concept implique que, pour n'importe quelle orientation d'un objet, un point d'appui peut tre localis , o l'objet est en quilibre. Chacun de ces points correspond une ligne verticale. En r p tant ce processus avec diff rentes orientations de l'objet, il devient vident que les lignes verticales se croisent en un point sp cifique l'int rieur de l'objet. Ce point est appel centre de masse (CM). En essence, le centre de masse est le point unique l'int rieur de l'objet o , quelle que soit son orientation, l' quilibre est toujours atteint.
(ID 323)
On peut d finir le centre de masse comme le point o toutes les lignes verticales trac es travers les points o le syst me est en quilibre se croisent :
(ID 11603)
Tout corps qui se d place et tourne le fait de mani re ce que :
• son mouvement de translation puisse tre d crit comme si toute la masse tait concentr e au centre de masse,
• sa rotation s'effectue autour du centre de masse comme s'il n' tait pas en translation.
(ID 11604)
L'orientation du couple peut tre d termin e l'aide de la r gle de la main droite : si vous pointez vos doigts dans la direction du rayon et que vous tournez dans le sens de la force,
(ID 11602)
ID:(1416, 0)