Ground Flow
Storyboard 
In the case of soil, it can be modeled by assuming that it contains multiple pores that form small capillaries running through it. Based on this, equations for laminar flow through tubes can be applied, and the hydraulic resistances of capillary networks can be calculated. These resistances depend on the porosity and, thus, on the proportion of the different components.
ID:(370, 0)
Ground Flow
Description 
In the case of soil, it can be modeled by assuming that it contains multiple pores that form small capillaries running through it. Based on this, equations for laminar flow through tubes can be applied, and the hydraulic resistances of capillary networks can be calculated. These resistances depend on the porosity and, thus, on the proportion of the different components.
Variables
Calculations
Calculations
Equations
If we consider the area in the section that does not contain pores, subtracting the pore section ($S_p$) from the section Flow ($S$) and dividing it by the area of a generic grain with a radius of ERROR:10129,0, we obtain the number of visible grains in the cross-section:
$\displaystyle\frac{S-S_p}{\pi r_0^2}=\displaystyle\frac{(1-f)S}{\pi r_0^2}$
where we use the relation for the porosity ($f$):
| $ f = \displaystyle\frac{ S_p }{ S }$ |
If the number of grains is equal to ERROR:6039,0 with the expression:
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
where the radius is the tube radius ($R$). With this, we obtain the relation:
$\displaystyle\frac{(1-f)S}{\pi r_0^2}=\displaystyle\frac{fS}{\pi R^2}$
resulting in:
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
(ID 109)
With the height the infinitesimal distance ($ds$), the volume of the section Flow ($S$) is
$S ds$
and the volume of the pores with the pore section ($S_p$) is
$S_p ds$
Therefore, the porosity ($f$) is calculated as
$f = \displaystyle\frac{S_p ds}{S ds} = \displaystyle\frac{S_p}{S}$
resulting in the following equation:
| $ f = \displaystyle\frac{ S_p }{ S }$ |
(ID 938)
The volume of the capillary can be calculated from the tube radius ($R$) and the capillary length ($l$), which is equal to the volume of a chain of grains of the radius of a generic grain ($r_0$) and the tube length ($\Delta L$) multiplied by the generic own porosity ($q_0$):
$\pi R^2 l = q_0 \pi r_0^2 \Delta L$
This, in conjunction with the porosity ($f$) in the relationship
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
results in the following relationship:
| $ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $ |
(ID 2215)
As the porosity ($f$), calculated with the pore section ($S_p$) and the section Flow ($S$) using
| $ f = \displaystyle\frac{ S_p }{ S }$ |
together with the equation for the calculation of the pore section ($S_p$) based on the number of capillaries ($N_p$) and the tube radius ($R$) through
| $ S_p = N_p \pi R ^2$ |
results in
$f = \displaystyle\frac{N_p\pi R^2}{S}$
can be solved for the number of capillaries ($N_p$), yielding
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
(ID 4363)
To calculate the total flow ($J_{Vt}$) using the number of capillaries ($N_p$) and the volume flow ($J_V$) for each capillary through
| $ J_{Vt} = N_p J_V $ |
we obtain the number of capillaries ($N_p$) with the porosity ($f$), the section Flow ($S$), and the tube radius ($R$) through
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
and the Hagen-Poiseuille law using the viscosity ($\eta$), the pressure difference ($\Delta p$), and the capillary length ($l$) is calculated with
$J_v = - \displaystyle\frac{\pi R^4}{8\eta}\displaystyle\frac{\Delta p}{l}$
Using the relationship for the tube radius ($R$) in terms of the radius of a generic grain ($r_0$)
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
and for the capillary length ($l$), the generic own porosity ($q_0$), and the sample length ($\Delta L$)
| $ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $ |
we obtain
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
(ID 4365)
In the case of capillaries through which a liquid with the liquid density ($\rho_w$) flows due to the pressure difference ($\Delta p$) generated by ERROR:5446.1 under the influence of gravity represented by the gravitational Acceleration ($g$) and calculated with the equation:
| $ \Delta p = \rho_w g \Delta h $ |
this can be applied in the Hagen-Poiseuille equation, in terms of the total flow ($J_{Vt}$), which in turn depends on the radius of a generic grain ($r_0$), the generic own porosity ($q_0$), the porosity ($f$), the viscosity ($\eta$), the section or Area ($S$), and the sample length ($\Delta L$) as described in the equation:
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
Together with the definition of the flux density ($j_s$):
$j_s = \displaystyle\frac{J_{Vt}}{S}$
We have:
$j_s=\displaystyle\frac{J_{Vt}}{S}=\displaystyle\frac{ r_0 ^2 }{8 q_g }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ L }$
resulting in:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
(ID 4366)
Since the flux density ($j_s$) is related to the radius of a generic grain ($r_0$), the porosity ($f$), the liquid density ($\rho_w$), the gravitational Acceleration ($g$), the viscosity ($\eta$), the generic own porosity ($q_0$), the height difference ($\Delta h$), and the sample length ($\Delta L$) through the equation:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
We can define a factor that we'll call the hydraulic conductivity ($K_s$) as follows:
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
This factor encompasses all the elements related to the properties of both the soil and the liquid that flows through it.
(ID 4739)
With Darcy's law, where the pressure difference ($\Delta p$) equals the hydraulic resistance ($R_h$) and the total flow ($J_{Vt}$):
| $ \Delta p = R_h J_V $ |
Thus, with the equation for the soil with the section Flow ($S$), the radius of a generic grain ($r_0$), the viscosity ($\eta$), the generic own porosity ($q_0$), the porosity ($f$), the pressure difference ($\Delta p$), and the sample length ($\Delta L$):
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
Therefore, the hydraulic resistance ($R_h$) is:
| $ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$ |
(ID 10594)
Examples
(ID 15203)
The individual pores come together to form chains that create capillaries through which water flows.
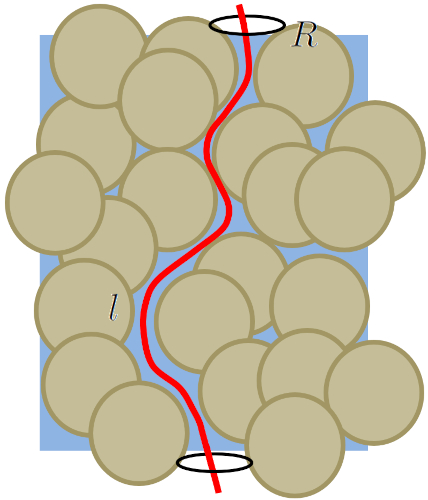
To model this phenomenon, it is necessary to estimate both the radius of these capillaries and their length, considering that they are typically not straight.
(ID 937)

(ID 2284)
The section Flow ($S$) includes the pore section ($S_p$) generated by the number of capillaries ($N_p$):
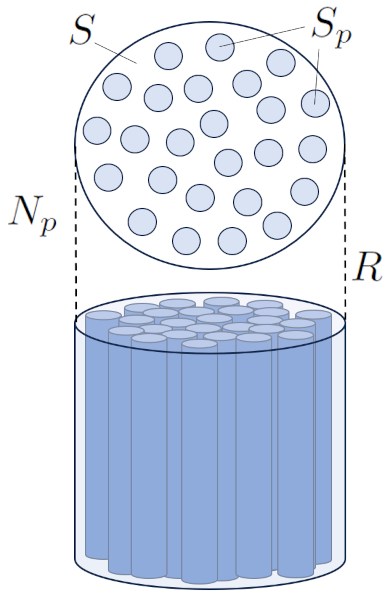
None
(ID 2285)
If we observe a cross-section of the soil, we'll notice that capillaries pass through the spaces between the grains. By doing so, their number is similar to that of the grains themselves, so we can assume that the number of capillaries ($N_p$) is similar to the number of grains present in the cross-section:
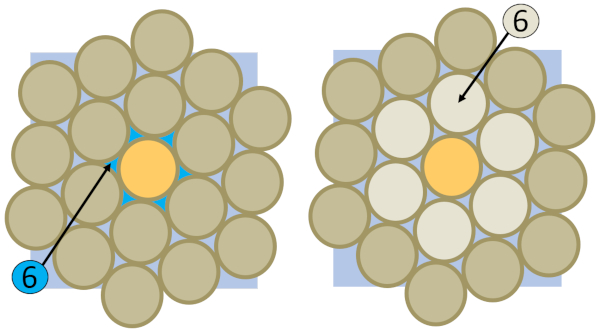
None
(ID 2283)

(ID 2291)
The total flow is calculated as the sum of the individual flows through the different pores:
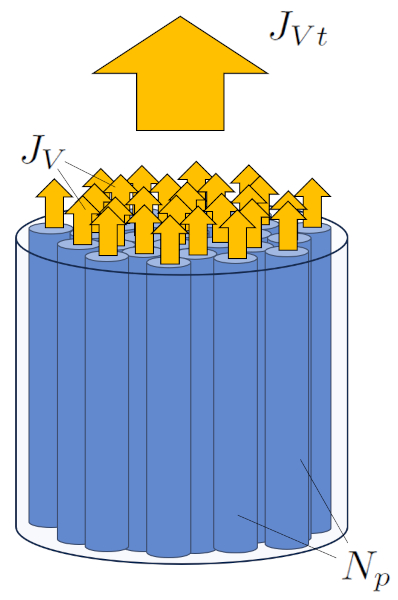
None
If we assume that all the pores are identical, we can obtain the total flow ($J_{Vt}$) by multiplying the volume flow ($J_V$) individually by the number of capillaries ($N_p$).
(ID 2286)
If we examine the literature, we can find estimates of hydraulic conductivity for different soil textures, which are shown here as a function of their exponent (i.e., -7 is indicated for a hydraulic conductivity of 1E-7 m/s):
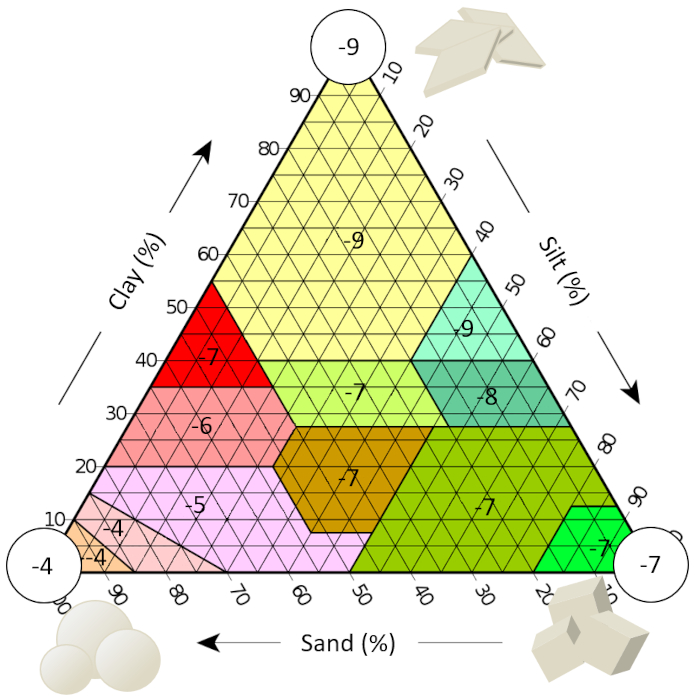
The results are summarized in the following table:
| Texture | $g_a$ [%] | $g_i$ [%] | $g_c$ [%] | $f$ [%] | $K$ [m/s] |
| Clay | 0-45 | 0-40 | 55-100 | 40-50 | 1E-9 - 1E-8 [1] |
| Loam | 23-52 | 28-50 | 8-27 | 40-50 | 1E-7 - 1E-5 [2] |
| Sand | 85-100 | 0-15 | 0-10 | 25-35 | 1E-4 - 1E-2 [3] |
| Silt | 0-20 | 80-100 | 0-13 | 35-45 | 1E-7 - 1E-5 [4] |
| Silty Clay | 0-20 | 40-60 | 40-60 | 40-50 | 1E-9 - 1E-8 [1] |
| Sandy Clay | 45-65 | 0-20 | 35-55 | 35-45 | 1E-7 - 1E-5 [5] |
| Sandy Loam | 20-45 | 15-53 | 28-40 | 40-50 | 1E-7 - 1E-5 [2] |
| Clayey Silt | 0-20 | 40-73 | 28-40 | 40-50 | 1E-8 - 1E-6 [6] |
| Sandy Clayey Loam | 45-80 | 0-33 | 20-35 | 35-45 | 1E-6 - 1E-4 [1] |
| Silt Loam | 0-50 | 50-88 | 0-28 | 35-45 | 1E-7 - 1E-5 [4] |
| Sandy Loam | 43-85 | 0-50 | 0-20 | 30-40 | 1E-5 - 1E-3 [2] |
| Sandy Silty Loam | 70-90 | 0-30 | 0-15 | 25-35 | 1E-4 - 1E-2 [4] |
These data were obtained from the following literature, which is referenced in the hydraulic conductivity column:
[1] "Geotechnical Engineering Principles and Practices" by Donald P. Coduto et al., Prentice Hall (1999)
[2] "Soil Mechanics and Foundations" by Muni Budhu, John Wiley & Sons. (2011)
[3] "Introduction to Environmental Engineering" by Mackenzie Davis and David Cornwell, McGraw Hill (2022)
[4] "Principles of Geotechnical Engineering" by Braja M. Das, CL-Engineering (2009)
[5] "Soil Mechanics in Engineering Practice" by Karl Terzaghi and Ralph B. Peck, John Wiley & Sons. (1996)
[6] "Soil Mechanics: Concepts and Applications" by William Powrie, CRC Press (2013)
(ID 4740)
(ID 15222)
ID:(370, 0)
