Flow through multiple layers
Storyboard 
Once the hydraulic resistance and conductivity have been calculated, it becomes possible to model a multi-layer soil system. To achieve this, it is essential to compute the total resistance and conductivity and, after establishing the overall flow, to determine the partial flows (in the case of parallel layers) or the pressure drop in each layer (in the case of series layers).
ID:(371, 0)
Flow through multiple layers
Description 
Once the hydraulic resistance and conductivity have been calculated, it becomes possible to model a multi-layer soil system. To achieve this, it is essential to compute the total resistance and conductivity and, after establishing the overall flow, to determine the partial flows (in the case of parallel layers) or the pressure drop in each layer (in the case of series layers).
Variables
Calculations
Calculations
Equations
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
| $ J_V = G_h \Delta p $ |
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
results in:
| $ \Delta p = R_h J_V $ |
(ID 3179)
One way to model a tube with varying cross-section is to divide it into sections with constant radius and then sum the hydraulic resistances in series. Suppose we have a series of the hydraulic resistance in a network ($R_{hk}$), which depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) via the following equation:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
In each segment, there will be a pressure difference in a network ($\Delta p_k$) with the hydraulic resistance in a network ($R_{hk}$) and the volume flow ($J_V$) to which Darcy's Law is applied:
| $ \Delta p = R_h J_V $ |
the total pressure difference ($\Delta p_t$) will be equal to the sum of the individual ERROR:10132,0:
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
therefore,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Thus, the system can be modeled as a single conduit with the hydraulic resistance calculated as the sum of the individual components:
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
(ID 3180)
The parallel total hydraulic conductance ($G_{pt}$) combined with the hydraulic conductance in a network ($G_{hk}$) in
| $ G_{pt} =\displaystyle\sum_k G_{hk} $ |
and along with the hydraulic resistance in a network ($R_{hk}$) and the equation
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
leads to the total hydraulic resistance in parallel ($R_{pt}$) via
| $\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$ |
(ID 3181)
The total hydraulic resistance in series ($R_{st}$), along with the hydraulic resistance in a network ($R_{hk}$), in
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
and along with the hydraulic conductance in a network ($G_{hk}$) and the equation
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
leads to the total Series Hydraulic Conductance ($G_{st}$) can be calculated with:
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$ |
(ID 3633)
With the total flow ($J_{Vt}$) being equal to the volume flow in a network ($J_{Vk}$):
| $ J_{Vt} =\displaystyle\sum_k J_{Vk} $ |
and with the pressure difference ($\Delta p$) and the hydraulic conductance in a network ($G_{hk}$), along with the equation
| $ J_V = G_h \Delta p $ |
for each element, it leads us to the conclusion that with the parallel total hydraulic conductance ($G_{pt}$),
$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$
we have
| $ G_{pt} =\displaystyle\sum_k G_{hk} $ |
.
(ID 3634)
Since the flux density ($j_s$) is related to the radius of a generic grain ($r_0$), the porosity ($f$), the liquid density ($\rho_w$), the gravitational Acceleration ($g$), the viscosity ($\eta$), the generic own porosity ($q_0$), the height difference ($\Delta h$), and the sample length ($\Delta L$) through the equation:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
We can define a factor that we'll call the hydraulic conductivity ($K_s$) as follows:
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
This factor encompasses all the elements related to the properties of both the soil and the liquid that flows through it.
(ID 4739)
As the hydraulic resistance ($R_h$) is associated with the hydraulic conductivity ($K_s$), the liquid density ($\rho_w$), the gravitational Acceleration ($g$), the column Section ($S$), and the sample length ($\Delta L$), it is expressed as
| $ R_h = \displaystyle\frac{ \rho_w g }{ K_s }\displaystyle\frac{ \Delta L }{ S }$ |
And the relationship for the hydraulic conductance ($G_h$)
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
leads to
| $ G_h = \displaystyle\frac{ K_s }{ \rho_w g }\displaystyle\frac{ S }{ \Delta L }$ |
(ID 10592)
With Darcy's law, where the pressure difference ($\Delta p$) equals the hydraulic resistance ($R_h$) and the total flow ($J_{Vt}$):
| $ \Delta p = R_h J_V $ |
Thus, with the equation for the soil with the section Flow ($S$), the radius of a generic grain ($r_0$), the viscosity ($\eta$), the generic own porosity ($q_0$), the porosity ($f$), the pressure difference ($\Delta p$), and the sample length ($\Delta L$):
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
Therefore, the hydraulic resistance ($R_h$) is:
| $ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$ |
(ID 10594)
Calculating the hydraulic resistance ($R_h$) using the viscosity ($\eta$), the generic own porosity ($q_0$), the radius of a generic grain ($r_0$), the porosity ($f$), the sample length ($\Delta L$), and the column Section ($S$) through
| $ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$ |
and utilizing the expression for the hydraulic conductivity ($K_s$)
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
is obtained after replacing the common factors
| $ R_h = \displaystyle\frac{ \rho_w g }{ K_s }\displaystyle\frac{ \Delta L }{ S }$ |
(ID 10635)
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
to arrive at:
| $ J_V = G_h \Delta p $ |
(ID 14471)
Examples
(ID 15204)
In the case of a sum where the elements are connected in series, the total hydraulic resistance of the system is calculated by summing the individual resistances of each element.

One way to model a tube with varying cross-section is to divide it into sections with constant radius and then sum the hydraulic resistances in series. Suppose we have a series of the hydraulic resistance in a network ($R_{hk}$), which depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) via the following equation:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
In each segment, there will be a pressure difference in a network ($\Delta p_k$) with the hydraulic resistance in a network ($R_{hk}$) and the volume flow ($J_V$) to which Darcy's Law is applied:
| $ \Delta p = R_h J_V $ |
the total pressure difference ($\Delta p_t$) will be equal to the sum of the individual ERROR:10132,0:
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
therefore,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Thus, the system can be modeled as a single conduit with the hydraulic resistance calculated as the sum of the individual components:
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
(ID 3630)
In the case of a sum where the elements are connected in series, the total hydraulic conductance of the system is calculated by adding the individual hydraulic conductances of each element.
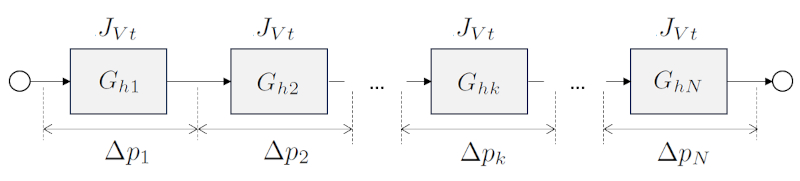
the total hydraulic resistance in series ($R_{st}$), along with the hydraulic resistance in a network ($R_{hk}$), in
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
and along with the hydraulic conductance in a network ($G_{hk}$) and the equation
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
leads to the total Series Hydraulic Conductance ($G_{st}$) can be calculated with:
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$ |
$\Delta p_k = \displaystyle\frac{J_{Vk}}{K_{hk}}$
So, the sum of the inverse of the hydraulic conductance in a network ($G_{hk}$) will be equal to the inverse of the total Series Hydraulic Conductance ($G_{st}$).
(ID 11067)
A situation in the soil where the elements are connected in series occurs when water infiltrates vertically through several layers, eventually ending up in the water table. In this case, the column Section ($S$) remains constant, while each layer has a different width that acts as the width of the kth layer ($L_k$).
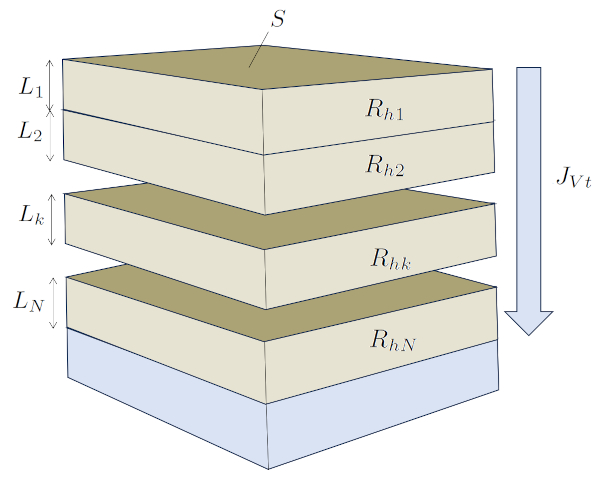
In this scenario, hydraulic resistances are directly summed, and their values depend on the type of soil, and therefore, on the hydraulic conductivity in the kth layer ($K_{sk}$) and the width of the kth layer ($L_k$).
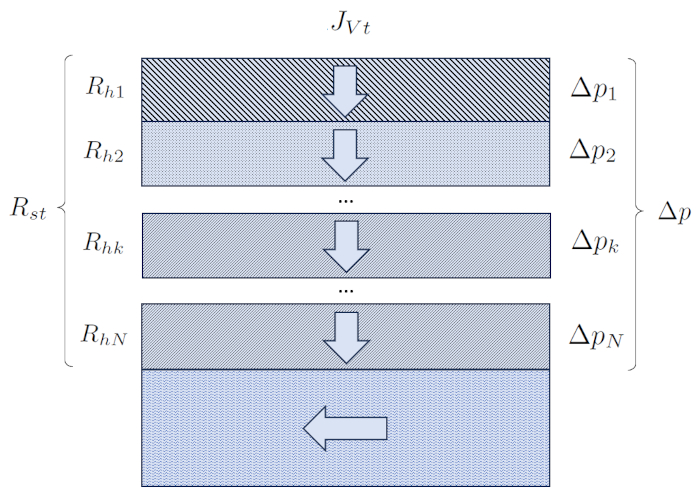
(ID 936)
One efficient way to model a tube with varying cross-sections is to divide it into sections with constant radii and then sum the hydraulic resistances in series. Suppose we have a series of elements the hydraulic resistance in a network ($R_{hk}$), whose resistance depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$), according to the following equation:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
In each element, we consider a pressure difference in a network ($\Delta p_k$) along with the hydraulic resistance in a network ($R_{hk}$) and the volumetric flow rate the volume flow ($J_V$), where Darcy's law is applied:
| $ \Delta p = R_h J_V $ |
The total resistance of the system, the flujo de Volumen Total ($J_{Vt}$), is equal to the sum of the individual hydraulic resistances ERROR:10133,0 of each section:
| $ J_{Vt} =\displaystyle\sum_k J_{Vk} $ |
Thus, we have:
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Therefore, the system can be modeled as a single conduit with a total hydraulic resistance calculated by summing the individual components:
| $\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$ |
(ID 11068)
A situation in the soil where the elements are connected in parallel occurs when water flows through different layers in parallel. If the layers have a slope, a pressure difference is generated. If the layers have a similar thickness, the pressure difference will be the same in all layers. In this case, the sample length ($\Delta L$) is constant, while each layer has a different the section of the kth layer ($S_k$).
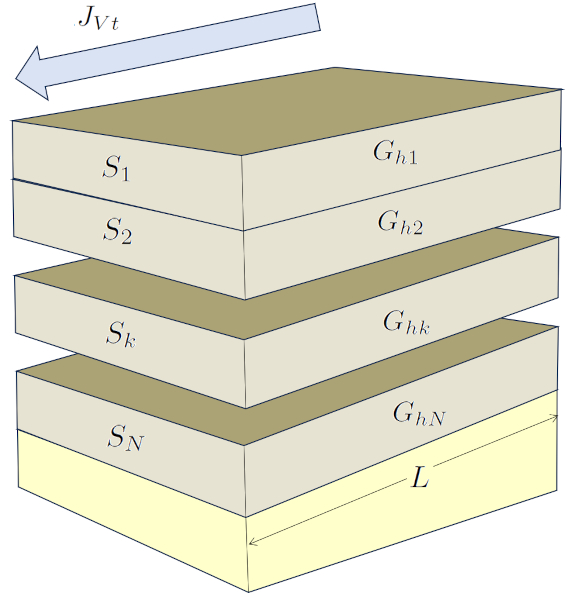
In this situation, hydraulic conductivities are directly summed, and their values depend on the type of soil, and therefore, on the hydraulic conductivity in the kth layer ($K_{sk}$) and the section of the kth layer ($S_k$).
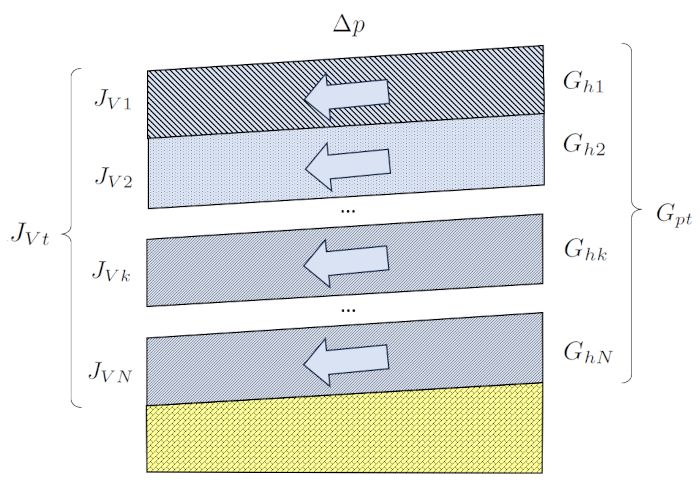
(ID 4373)
(ID 15223)
ID:(371, 0)
