Druyd:Knowledge

Modelo SEIR

Storyboard

ID:(349, 0)

Modelos SEIR modificados

Definición

Modelos que incluyen los casos en que existen personas infectadas pero que aun no muestran síntomas y no contagian. Dichas personas se denominan personas latentes.

ID:(873, 0)

Curva del modelo SEIR

Imagen

ID:(9703, 0)

Modelo SEIR

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$R_0$

R_0

Factor de Recuperación

$I_{crit}$

I_crit

Infectados Críticos

$I_t$

I_t

Infectados Totales al tiempo $t$

$E$

Latentes

$E_{crit}$

E_crit

Latentes Asimptótica

$C$

Número de Personas con que se Contacta

$N$

Población

$\beta$

beta

Probabilidad de Contagio por tiempo

1/s

$R_t$

R_t

Recuperados Totales al tiempo $t$

$S_{crit}$

S_crit

Susceptibles Críticos

$S_t$

S_t

Susceptibles Totales al tiempo $t$

$\mu_d$

mu_d

Tasa de Muerte por tiempo

$\mu_b$

mu_b

Tasa de Nacimiento por tiempo

$\sigma$

sigma

Tasa de Paso de Latente a Infectado por Tiempo

$\gamma$

gamma

Tasa de Recuperación por tiempo

1/s

$dI$

Variación de Infectados

$dE$

Variación de Latentes

$dR$

Variación de Recuperados

$dS$

Variación de Susceptibles

$dt$

Variación infinitesimal del tiempo

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

dS/dt=-(beta C/N)I(t)S(t)+mu_bN-mu_dS(t)

(ID 4086)

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

dE/dt=(beta C/N)I(t)S(t)-(sigma+mu_d)E(t)

(ID 4087)

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

dI/dt=sigma E(t)-(gamma+mu_d)I(t)

(ID 4088)

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

dR/dt=gamma I(t)-mu_dR(t)

(ID 4089)

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$

S_crit/N=(sigma+mu_d)(gamma+mu_d)/(beta C sigma)

(ID 4090)

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$

I_crit/N=(mu_bN-mu_dS_crit)/(beta C S_crit)

(ID 4091)

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$

E_crit/N=((gamma+mu_d)/sigma)I_crit/N

(ID 4092)

$R_0=\displaystyle\frac{\beta C\sigma}{(\sigma+\mu_d)(\gamma+\mu_d)}$

R_0=(beta C sigma)/((sigma+mu_d)(gamma+mu_d))

(ID 4093)

Ejemplos

Modelos SEIR modificados

Modelos que incluyen los casos en que existen personas infectadas pero que aun no muestran s ntomas y no contagian. Dichas personas se denominan personas latentes.

(ID 873)

Curva del modelo SEIR

En el caso de los modelos SEIR se tienen cuatro curvas, la de susceptibles, latentes, infectados y recuperados:

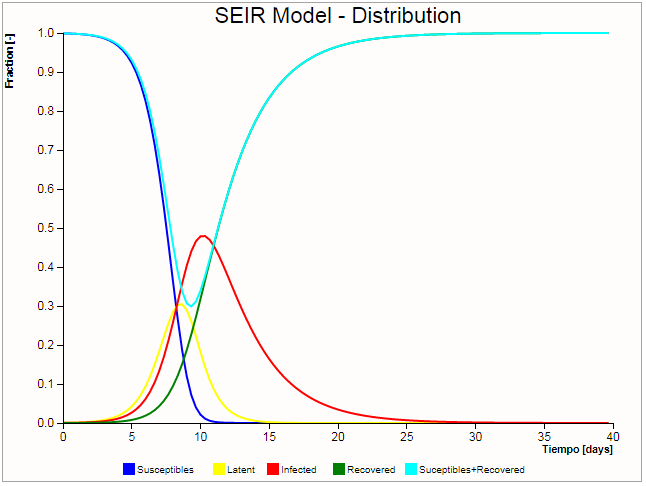
(ID 9703)

Simulaci n del modelo SEIR

El modelo se puede resolver num ricamente las ecuaciones para los susceptibles S, infectados I, latentes E y recuperados R:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

en donde t es el tiempo \beta la taza de contagio, \sigma la taza de surgimiento de los s ntomas en los infectados, \gamma la taza de recuperaci n, C el n mero de contactos, N la poblaci n, \mu_b la natalidad por habitante y \mu_d la mortalidad por habitante.

(ID 6834)

ID:(349, 0)