Usuario:
Derivadas & Diferenciales
Definición 
Construcción de diferenciales tanto exactos como inexactos en base a derivadas ordinarias y parciales.
ID:(565, 0)
Derivadas Parciales
Nota
En el caso de que la función depende de más de una variable es necesario generalizar el concepto de derivada parcial.
La forma mas simple es continuar con la misma definición anterior pero asumir que las demas variables se mantienen constantes.
A modo de ejemplo consideremos la función de dos variables $f(x,y)$. Supongamos que deseamos derivar respecto de $x$. El resultado puede variar si en el proceso de derivar el valor de $y$ se altera. Distinta es la situación si formzamos que $y$ se mantenga fijo $($constante$)$.
Para recordar que estamos realizando la derivada con la condición de que las restantes variables no se alteran $($o sea $y$ permanece fijo$)$ empelamos una $d$ distinta: $\partial$ $($$\partial$ es una $d$ griega$)$.
Por ello en este caso pasaremos de
$\displaystyle\frac{df}{dx}\rightarrow\displaystyle\frac{\partial f}{\partial x}\equiv f_x$
o correspondientemente
$\displaystyle\frac{df}{dy}\rightarrow\displaystyle\frac{\partial f}{\partial y}\equiv f_y$
ID:(563, 0)
Differentials y Ecuaciones Diferenciales
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 3462)
(ID 3463)
(ID 3464)
(ID 3466)
Ejemplos
Construcci n de diferenciales tanto exactos como inexactos en base a derivadas ordinarias y parciales.
(ID 565)
Funciones de dos Variables
(ID 1882)
En el caso de que la funci n depende de m s de una variable es necesario generalizar el concepto de derivada parcial.
La forma mas simple es continuar con la misma definici n anterior pero asumir que las demas variables se mantienen constantes.
A modo de ejemplo consideremos la funci n de dos variables $f(x,y)$. Supongamos que deseamos derivar respecto de $x$. El resultado puede variar si en el proceso de derivar el valor de $y$ se altera. Distinta es la situaci n si formzamos que $y$ se mantenga fijo $($constante$)$.
Para recordar que estamos realizando la derivada con la condici n de que las restantes variables no se alteran $($o sea $y$ permanece fijo$)$ empelamos una $d$ distinta: $\partial$ $($$\partial$ es una $d$ griega$)$.
Por ello en este caso pasaremos de
$\displaystyle\frac{df}{dx}\rightarrow\displaystyle\frac{\partial f}{\partial x}\equiv f_x$
o correspondientemente
$\displaystyle\frac{df}{dy}\rightarrow\displaystyle\frac{\partial f}{\partial y}\equiv f_y$
(ID 563)
Interpretaci n de Diferenciales Inexactos
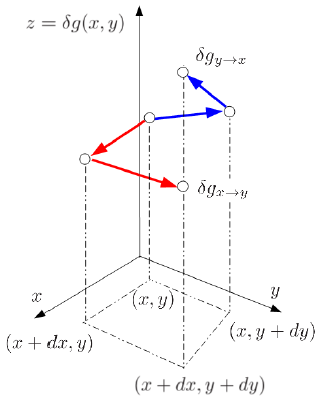
(ID 1883)
ID:(432, 0)