Benützer:


Zusammenfassung der Monte Carlo Methode (MCM)
Storyboard

Obwohl die Monte-Carlo-Methode (MCM) als Goldstandard in der Dosisberechnung angesehen wird, ist ihre Anwendung durch den Rechenaufwand begrenzt. Dies hängt mit der großen Anzahl von Partikeln zusammen, die simuliert werden müssen, um die numerische Unsicherheit zu reduzieren, die der Komplexität des Systems innewohnt. In dieser Übersicht wird die Methode beschrieben und das Problem der numerischen Unsicherheit erklärt.

>Modell

ID:(1161, 0)


Random Walk
Bild

>Top


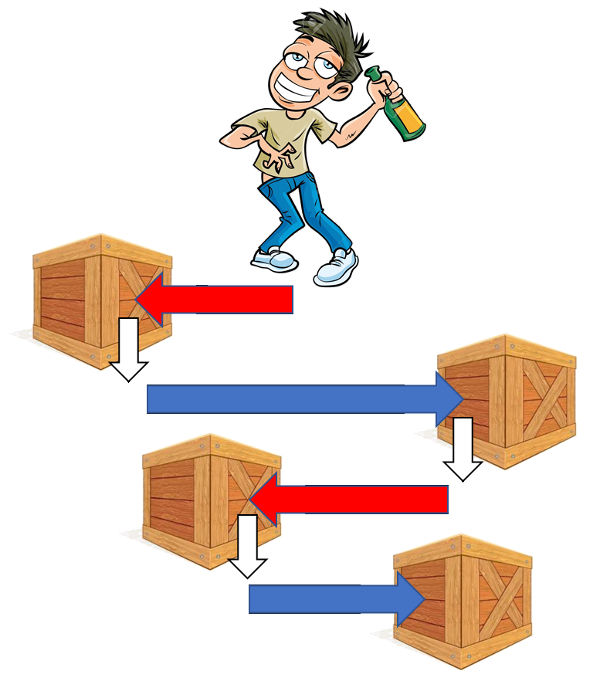
Um die Eigenschaften von Monte Carlo zu erforschen, nehmen wir an, dass wir das Verhalten eines Betrunkenen simulieren wollen.

Er bewegt sich unidimensional und kann nach rechts und nach links gehen.

Die Distanzen, die in jeder Richtung zurückgelegt wird, hängen von den Objekten auf dem Weg ab. Diese werden nach dem Zufallsprinzip verteilt.

Jedes Mal, wenn er ein Objekt erreicht, kehrt er in die umgekehrte Richtung zurückt.

ID:(9175, 0)


Random walk mit variabler Schrittlänge
Gleichung

>Top, >Modell


Der einfachste Fall ist der einer Partikel die sich entlang einer Achse bewegt und die nach einem Zusammenstoß mit einem Objekt die Bewegungsrichtung umkehrt.

Wenn die Wahrscheinlichkeit ein Abstand zwischen x und x + dx zu erreichen gleich P(x) ist, dann ist die Wahrscheinlichkeit des Zusammenstoßes

P(x)-P(x+dx)\sim-\display\frac{dP}{dx}dx

Falls diese Wahrscheinlichkeit proportional zur Wahrscheinlichkeit P ist, ergibt sich dass

\display\frac{dP}{dx}=-\display\frac{dx}{\lambda}P(x)

So folgt, dass

$p(x)dx = \displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx$

wobei \lambda der freie Weg ist.

ID:(9099, 0)


Simulador random walk paso variable
Php

>Top


Um die Verteilung der Positionen der Teilchen zu erhalten, kann folgende Iterationen durchgeführt werden

```

0. Position und Startadresse definiert

1. Partikel in eine Richtung bewegen in einem Abstand der durch die Zufallswahrscheinlichkeitsfunktion erzeugt wird,

2. Richtung umkehren

3. Fortsetzung 1

```

Angenommen, wir eine bestimmte Zeit und das sich das Teilchen mit einer konstanten Geschwindigkeit bewegt. Somit kam die Position nach einer Zeit oder einem zurück gelegten Weg bestimmt werden.

ID:(9100, 0)


Zusammenfassung
Beschreibung

>Top


Mit dem Simulator zu spielen, haben wir das bemerkt

```

1. Es ist nur sinnvoll, Verteilungen von möglichen Positionen zu betrachten

2. Die Verteilung basiert auf der Bestimmung von Positionen in diskreten Bereichen

3. Bereiche kleinerer Größe erfordern eine größere Anzahl von Iterationen

```

ID:(9101, 0)


Total effektiver Gesamtquerschnitt und freier Weg
Gleichung

>Top, >Modell


Der gesamte effektive Querschnitt \sigma bezieht sich auf den effektiven Abschnitt, den das Teilchen dem einfallenden Strahl anbietet und somit direkt auf den freien Weg wirkt. Wenn es mit der Konzentration der Teilchen c multipliziert wird, kann man sich zeigen, dass der freie Weg ist

$\lambda=\displaystyle\frac{1}{c\,\sigma}$

Mit denen es möglich ist, die Wahrscheinlichkeit der Auswirkungen mit dem insgesamt effektiven Abschnitt abzuschätzen:

ID:(9178, 0)


Compton Scattering
Bild

>Top


Compton-Streuung tritt auf, wenn ein Photon mit einer geladenen Teilchen in Wechselwirkung tritt, insbesondere mit einem Elektron. Im Prozess Verliert das Photon Energie und weicht ab wobei das Elektron in Bewegung setzen:

ID:(9176, 0)


Compton Streuung
Gleichung

>Top, >Modell


Die Compton-Streuung tritt auf, wenn ein Photon mit einem Elektron wechselwirkt, indem es der erste Energie auf den zweite (unelastische Wechselwirkung) überträgt. Die Wellenlänge des Photon nach dem Scattering kann durch

$\lambda_2=\lambda+\lambda_c(1-\cos\theta)$



berechnet werden, wobei

$\lambda_c=\displaystyle\frac{h}{m_ec}$

die Compton Wellenlänge ist und \theta der Ablenkungswinkel des Photons ist.

ID:(9145, 0)


Differentialquerschnitt für die Compton-Streuung
Gleichung

>Top, >Modell


Für Compton-Streuung ist der Differentialquerschnitt gemäß Klein-Nishina

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



wobei

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



der Gesamtquerschnitt von Thomson und

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

die normierte Energie ist.

ID:(9144, 0)


Gesamtquerschnitt für die Compton-Streuung
Gleichung

>Top, >Modell


Wenn der Differentialwirkungsabschnitt nach Klein-Nishina genommen wird

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



und integriert wird im Raumwinkel



wobei

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



der effektive Gesamtquerschnitt nach Thomson und

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

die normalisierte Energie ist.

Im Rahmen der kleinen \epsilon\ll1 ist der gesamtquerschnitt

\sigma_{KN}\sim\sigma_T\left(1-2\epsilon+\displaystyle\frac{26}{5}\epsilon^2\ldots\right)

und im Fall \epsilon\gg 1 muss der gleich

\sigma_{KN}\sim\displaystyle\frac{3}{8}\displaystyle\frac{\sigma_T}{\epsilon}\left(\log(2\epsilon)+\displaystyle\frac{1}{2}\right)

sein.

ID:(9111, 0)


Simulador random walk con Compton
Php

>Top


Sie können die Klein-Nishina Modell numerisch untersuchen. Für dies wird gezeigt

- der Gesamtquerschnitt als Funktion der Photonenenergie

- der Differentialabschnitt in Funktion des Winkel für die minimale, mittlere und maximale definierte Energien

- der effektive Gesamtquerschnitt als Funktion der Energie in einem eindimensionalen das Transmission oder Reflexion ergeben könnte

ID:(9114, 0)