Zusammenfassung der Lattice Boltzmann Methode (LBM)
Storyboard 
Die Lattice Boltzmann Methode (LBM) wurde geschaffen, um die Bearbeitungszeit bei der Lösung von hydro- und aerodynamischen Problemen zu reduzieren. Anstatt die Navier-Stokes-Differentialgleichung zu lösen, verwendet sie eine äquivalente Darstellung auf Basis der Boltzmann-Transportgleichung und reduziert den Verarbeitungsaufwand durch die Arbeit mit einem vereinfachten diskreten Phasenraum. Das Ergebnis ist ein Hochgeschwindigkeits-Simulator, der in der Lage ist, hochkomplexe Prozesse zu beschreiben.
ID:(1162, 0)
Lattice Boltzmann Method
Definition 
Das Problem mit Makro-Skalensystemen, die auf mikroskopischen Phänomenen basieren, ist das
- makroskopische Modelle sind zu einfach, um die Dynamik korrekt wiederzugeben
- mikroskopische Modelle zur Beschreibung der makroskopischen Wirklichkeit können nicht analytisch gelöst werden und numerische Lösungen sind schwerfällig (= erfordern viel rechnerische Ressourcen)
Die Boltzmann-Gittermethode sucht einen Zwischenpfad. Es basiert auf der Boltzmann-Transportgleichung, rettet den mikroskopischen Teil über den Kollisionstermin und implementiert eine vereinfachte Struktur zur Berechnung der makroskopischen Ergebnisse. Wir sprechen von einem mesoskopischen Ansatz wo wir nach Bedarf die mikroskopische Anstrengung reduzieren können, indem wir die Genauigkeit verlieren, aber Ressourcen sparen oder die Genauigkeit verbessern, indem wir mehr Ressourcen investieren.
ID:(8488, 0)
D2Q9 Modelle (zweidimensionale, 9 Punkte)
Bild 
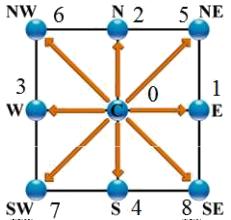
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gráfica:
ID:(8496, 0)
D3Q15 Modelle (dreidimensionale, 15 Punkte)
Notiz 
Das D3Q15 Modell ist ein zweidimensionales Modell (D3), in dem der Knoten (Punkt center) Knoten entlang der kartesischen Achsen verbindet\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)$
\\n\\nund in den Ecken des Würfels\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
was es in der folgenden Grafik dargestellt ist:
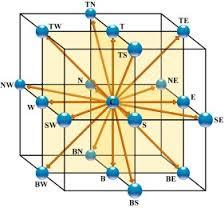
Es ist relativ einfach Modelle zu bauen vom Typ D3Q19 (einschließlich der Hälften der Seitenkanten ) oder D3Q27 (alle möglichen Punkte).
ID:(8497, 0)
Rückprall in Wänden orthogonal zu dem Netzwerk
Zitat 
Wenn der Rückprall nicht an einem Punkt des Netzes sondern in einem Abstand
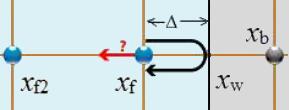
\\n\\ndann sollte die Funktion die Beiträge der Abweichungen berücksichtigen\\n\\n
$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$
ID:(8499, 0)
Rückprall bei geneigte Wände
Übung 
Wenn die Wand eine Neigung haben bezüglich des Netzwerk es in einer komplexere Modellierung notwendig:
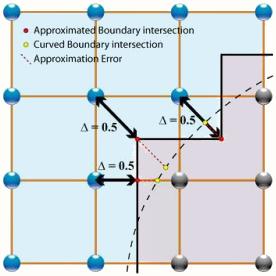
Allgemeine Umrandung
Zunächst muss eine ungefähre Grenze festgelegt werden um dann die entsprechende Gleichungen definiert werden. Diese wird dann innerhalb des Streamng Prozess angewandt.
ID:(8500, 0)
Beispiel von Streaming Gleichungen
Gleichung 
Im Falle eines D2Q9 Systems sind die 9 Werte ``` N[x,y] = N[x,y-1] NW[x,y] = NW[x+1,y-1] E[x,y] = E[x-1,y] NE[x,y] = NE[x-1,y-1] S[x,y] = S[x,y+1] SE[x,y] = SE[x-1,y+1] W[x,y] = W[x+1,y] SW[x,y] = SW[x+1,y+1] ```
ID:(9151, 0)
Ejemplo de elemento de Colisión
Script 
En el caso D2Q9 el termino colision se calcula sumando los distintos factores
| $f_i^{eq}=\rho\omega_i\left(1+\displaystyle\frac{3\vec{u}\cdot\vec{e}_i}{c}+\displaystyle\frac{9(\vec{u}\cdot\vec{e}_i)^2}{2c^2}-\displaystyle\frac{3u^2}{2c^2}\right)$ |
por lo que se tiene para cada celda
```
O = O+w(4rho/9)(1-3u2/2) - O)
E = E+w(rho/9)(1 + u_x/3+5u_x^2-3u2/2)-E)
W = W+w(rho/9)(1 - u_x/3+5u_x^2-3u2/2)-W)
N = N+w(rho/9)(1 + u_y/3+5u_y^2-3u2/2)-N)
S = S+w(rho/9)(1 - u_y/3+5u_y^2-3u2/2)-S)
NE = NE+w(rho/36)(1+u_x/3+u_y/3+5(u2+2u_xu_y)/2-3u2/2) - NE)
SE = SE+w(rho/36)(1+u_x/3-u_y/3+5(u2-2u_xu_y)/2-3u2/2) - SE)
NW = NW+w(rho/36)(1-u_x/3+u_y/3+5(u2-2u_xu_y)/2-3u2/2) - NW)
SW = SW+w(rho/36)(1-u_x/3-u_y/3+5(u2+2u_xu_y)/2-3u2/2) - SW)
```
con
```
u2 = u_x^2+u_y^2
```
ID:(9155, 0)
Ejemplo Simulador Hidrodinamico
Variable 
En el caso de partículas de un liquido el método LBM permite desarrollar simuladores como se muestra en el ejemplo:
ID:(9156, 0)
Zusammenfassung der Lattice Boltzmann Methode (LBM)
Storyboard 
Die Lattice Boltzmann Methode (LBM) wurde geschaffen, um die Bearbeitungszeit bei der Lösung von hydro- und aerodynamischen Problemen zu reduzieren. Anstatt die Navier-Stokes-Differentialgleichung zu lösen, verwendet sie eine äquivalente Darstellung auf Basis der Boltzmann-Transportgleichung und reduziert den Verarbeitungsaufwand durch die Arbeit mit einem vereinfachten diskreten Phasenraum. Das Ergebnis ist ein Hochgeschwindigkeits-Simulator, der in der Lage ist, hochkomplexe Prozesse zu beschreiben.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Boltzmann -Funktion beschreibt den Transport eines Partikelsystem durch die Verteilungsfunktion der Geschwindigkeit beschrieben:
wobei der Begriff
Wenn die Parameter durch Mittelung ber Geschwindigkeit berechnet werden
dann kann die Dichte wird durch Sch tzung Masse erhalten werden:
Wenn die Parameter durch die Mittelung ber Geschwindigkeit berechnet werden
dann ist die Str mungsgeschwindigkeit durch Integration der Geschwindigkeitsverteilung ber alle Geschwindigkeiten gegeben und wird durch:
berechnet.
Wenn die Parameter durch Mittelung ber Geschwindigkeit berechnet werden
und es ist der Gleichverteilungssatz betrachtet wird, kann die Temperatur durch die Integration der kinetische Energie durch die Verteilung der Geschwindigkeit durch die Gas Konstante geteilt gewichtet abgesch tzt werden:
Wenn die Parameter durch Mittelung ber Geschwindigkeit berechnet werden
dann wird der Spannungstensor wird durch Integration der Str mungsgeschwindigkeitsverteilung ber alle Geschwindigkeiten Gewichtung auf Geschwindigkeitsdifferenzen berechnet:
Das Problem mit Makro-Skalensystemen, die auf mikroskopischen Ph nomenen basieren, ist das
- makroskopische Modelle sind zu einfach, um die Dynamik korrekt wiederzugeben
- mikroskopische Modelle zur Beschreibung der makroskopischen Wirklichkeit k nnen nicht analytisch gel st werden und numerische L sungen sind schwerf llig (= erfordern viel rechnerische Ressourcen)
Die Boltzmann-Gittermethode sucht einen Zwischenpfad. Es basiert auf der Boltzmann-Transportgleichung, rettet den mikroskopischen Teil ber den Kollisionstermin und implementiert eine vereinfachte Struktur zur Berechnung der makroskopischen Ergebnisse. Wir sprechen von einem mesoskopischen Ansatz wo wir nach Bedarf die mikroskopische Anstrengung reduzieren k nnen, indem wir die Genauigkeit verlieren, aber Ressourcen sparen oder die Genauigkeit verbessern, indem wir mehr Ressourcen investieren.
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gr fica:
Das D3Q15 Modell ist ein zweidimensionales Modell (D3), in dem der Knoten (Punkt center) Knoten entlang der kartesischen Achsen verbindet\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)$
\\n\\nund in den Ecken des W rfels\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
was es in der folgenden Grafik dargestellt ist:
Es ist relativ einfach Modelle zu bauen vom Typ D3Q19 (einschlie lich der H lften der Seitenkanten ) oder D3Q27 (alle m glichen Punkte).
F r Diskretisierung in LBM arbeitet nicht Modelle mit Funktionen der Geschwindigkeit, wenn nicht mit diskreten Komponenten. So ist die Komponente
wobei
In Streaming Prozess werden die Partikel entlang ihrer Geschwindigkeitsrichtungen von benachbarten Zellen bewegen
wobei
Wenn der R ckprall nicht an einem Punkt des Netzes sondern in einem Abstand
$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$
Wenn die Wand eine Neigung haben bez glich des Netzwerk es in einer komplexere Modellierung notwendig:
Allgemeine Umrandung
Zun chst muss eine ungef hre Grenze festgelegt werden um dann die entsprechende Gleichungen definiert werden. Diese wird dann innerhalb des Streamng Prozess angewandt.
Im Falle eines D2Q9 Systems sind die 9 Werte ``` N[x,y] = N[x,y-1] NW[x,y] = NW[x+1,y-1] E[x,y] = E[x-1,y] NE[x,y] = NE[x-1,y-1] S[x,y] = S[x,y+1] SE[x,y] = SE[x-1,y+1] W[x,y] = W[x+1,y] SW[x,y] = SW[x+1,y+1] ```
En el caso D2Q9 el termino colision se calcula sumando los distintos factores
por lo que se tiene para cada celda
```
O = O+w(4rho/9)(1-3u2/2) - O)
E = E+w(rho/9)(1 + u_x/3+5u_x^2-3u2/2)-E)
W = W+w(rho/9)(1 - u_x/3+5u_x^2-3u2/2)-W)
N = N+w(rho/9)(1 + u_y/3+5u_y^2-3u2/2)-N)
S = S+w(rho/9)(1 - u_y/3+5u_y^2-3u2/2)-S)
NE = NE+w(rho/36)(1+u_x/3+u_y/3+5(u2+2u_xu_y)/2-3u2/2) - NE)
SE = SE+w(rho/36)(1+u_x/3-u_y/3+5(u2-2u_xu_y)/2-3u2/2) - SE)
NW = NW+w(rho/36)(1-u_x/3+u_y/3+5(u2-2u_xu_y)/2-3u2/2) - NW)
SW = SW+w(rho/36)(1-u_x/3-u_y/3+5(u2+2u_xu_y)/2-3u2/2) - SW)
```
con
```
u2 = u_x^2+u_y^2
```
In der Relaxationsn herung wird davon ausgegangen, dass die Verteilung
$\displaystyle\frac{df_i}{dt}=-\displaystyle\frac{f_i-f_i^{eq}}{\tau}$
die in der diskreten Approximation die Gleichung hat
wo der Begriff der Unterschiede in den Verteilungsfunktionen die Kollisionen darstellt.
Die Gleichgewichtsverteilung kann durch eine Maxwell-Boltzmann Verteilung angen hert werden,
wobei
En la aproximaci n Bhatnagar-Gross-Krook la distribuci n en equilibrio se asume como la de un gas de part culas sin interacci n
con
con
| Modelo | $\omega_i$ | Index |
| 1DQ3 | ? | i=0 |
| - | ? | i=1, 2 |
| 2DQ9 | 4/9 | i=0 |
| - | 1/9 | i=1,...,4 |
| - | 1/36 | i=5,...,8 |
| 3DQ15 | 1/3 | i=0 |
| - | 1/18 | i=1,...,6 |
| - | 1/36 | i=7,...,14 |
| 3DQ19 | ? | i=0 |
| - | ? | i=1,...,6 |
| - | ? | i=7,...,18 |
que se determinan asegurando que la distribuci n equilibrio cumpla las leyes de conservaci n.
En el caso de part culas de un liquido el m todo LBM permite desarrollar simuladores como se muestra en el ejemplo:
ID:(1162, 0)
