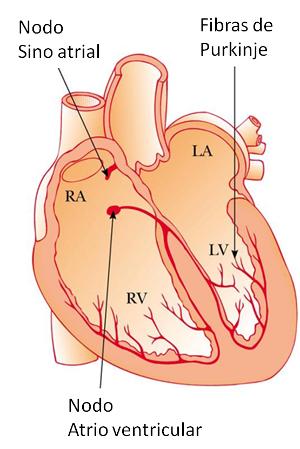
El coraz n funciona como un di-polo que va rotando.

Modelo del di-polo

image

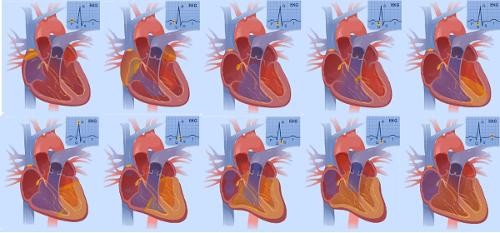
Electrocardiograma

image

Cardiograma y fase

image

La fuerza \vec{F} que representa matem ticamente como actual los campos el ctricos \vec{E} y magn ticos \vec{B} sobre una part cula se denomina la ley de Lorentz. Si la carga de la part cula es q y esta tiene una velocidad \vec{v} la fuerza de Lorentz ser

equation

La fuerza ($F$), que genera la densidad de flujo magnético ($B$) sobre la carga ($q$), el cual se desplaza bajo un angulo entre velocidad y campo magnético ($\theta$) con la velocidad ($v$), se expresa como:

kyon

La ecuaci n de movimiento resulta del equilibrio de la fuerza originada por la densidad de flujo magnético ($B$) sobre la carga ($q$) con la masa de la partícula ($m$) que viaja con la velocidad de la partícula ($v$) a el radio ($r$) de modo que

kyon

Polarizaci n

image

La rbita a un radio de giro de partícula en campo magnético ($r$) depende de la masa de la partícula ($m$), la velocidad ($v$), la carga ($Q$) y la densidad de flujo magnético ($B$), y se describe mediante la siguiente relaci n:

kyon