User:
Column of water in the sea
Storyboard 
In the case of the ocean, the density of water, depending on its temperature and salinity, varies with depth. For this reason the pressure cannot be calculated with the traditional pressure formula for the water column. It is necessary to consider the effect of the variation in density and calculate by integrating the mass along the column the pressure that occurs at the depth that we wish to estimate.
ID:(1598, 0)
Characterization of the ocean layers
Definition
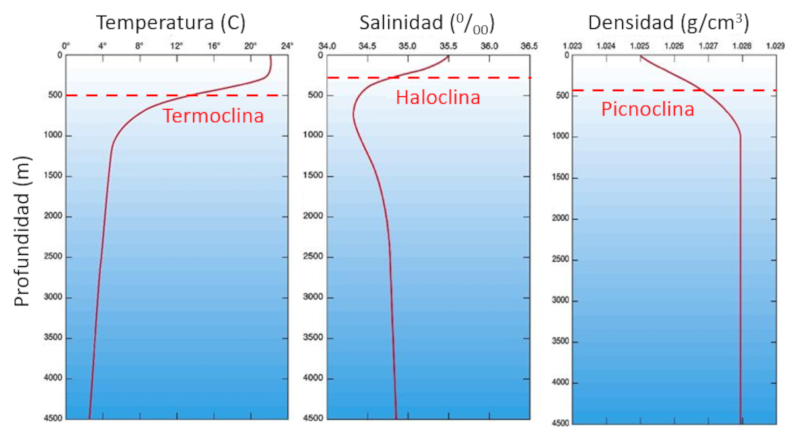
Ekman's transport causes the boundaries between the surface and deepest layers in the ocean to shift. These are characterized by sudden changes in parameters depending on the temperature. In particular there are changes in:
• Temperature (thermocline)
• Salinity (halocline)
• Density (pycnocline)
ID:(11684, 0)
Column with variable density
Image
To calculate the pressure under the sea at a given depth, one must first estimate the mass of a volume element at a certain depth:
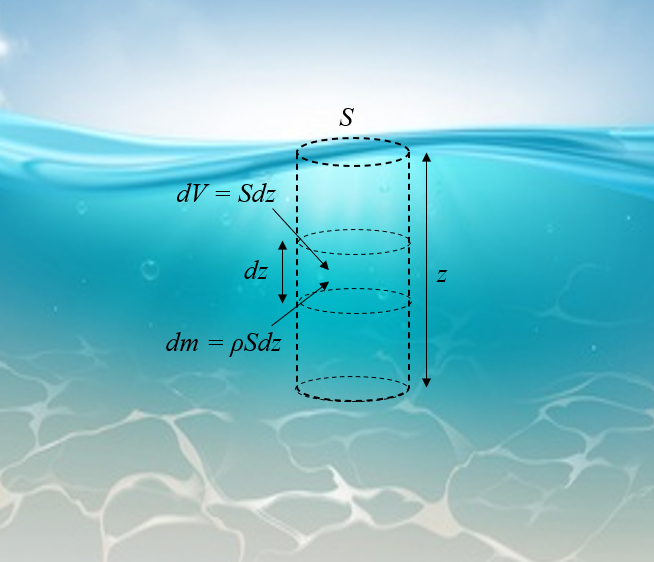
The problem in this case is that the density is not constant so the typical relationship of the pressure of the water column cannot be applied.
ID:(12008, 0)
Density modeling
Note
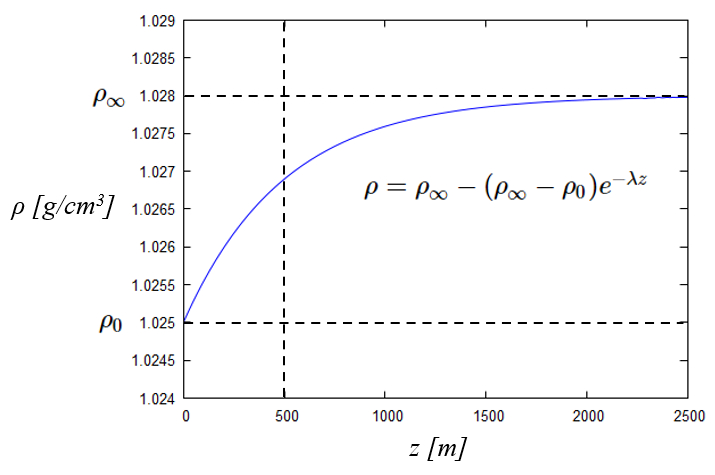
If you look at the curve of the density of ocean water as a function of depth, you see that it has the shape of an inverted exponential. In other words, the upper part is allowed to compress, reaching a limit where the weight of the column does not lead to greater compression:
ID:(12014, 0)
Column of water in the sea
Storyboard
In the case of the ocean, the density of water, depending on its temperature and salinity, varies with depth. For this reason the pressure cannot be calculated with the traditional pressure formula for the water column. It is necessary to consider the effect of the variation in density and calculate by integrating the mass along the column the pressure that occurs at the depth that we wish to estimate.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
Ekman's transport causes the boundaries between the surface and deepest layers in the ocean to shift. These are characterized by sudden changes in parameters depending on the temperature. In particular there are changes in:
• Temperature (thermocline)
• Salinity (halocline)
• Density (pycnocline)
To calculate the pressure under the sea at a given depth, one must first estimate the mass of a volume element at a certain depth:
The problem in this case is that the density is not constant so the typical relationship of the pressure of the water column cannot be applied.
A water element of a height
Con la definici n de la fuerza gravitacional
el aumento de la fuerza en funci n de la masa es
Con la variaci n de la masa
y la variaci n de la fuerza en funci n de la masa
con lo que se obtiene
Con la definici n de la presi n
la presi n aumenta con la fuerza seg n
en donde se asume que la secci n no varia.
Con la definici n de la presi n
el aumento de la fuerza
lleva a un aumento de la presi n
If you look at the curve of the density of ocean water as a function of depth, you see that it has the shape of an inverted exponential. In other words, the upper part is allowed to compress, reaching a limit where the weight of the column does not lead to greater compression:
If you observe the curve of density with depth you can model this with a value for surface density
Con el incremento de la presi n
se puede mediante integraci n calcular la presi n para cualquier profundidad:
Si se emplea la funci n de la densidad
en la ecuaci n de la presi n
se obtiene
ID:(1598, 0)