Benützer:
Wassersäule im Meer
Storyboard 
Im Falle des Ozeans variiert die Dichte des Wassers in Abhängigkeit von seiner Temperatur und seinem Salzgehalt mit der Tiefe. Aus diesem Grund kann der Druck nicht mit der herkömmlichen Druckformel für die Wassersäule berechnet werden. Es ist notwendig, den Effekt der Dichteschwankung zu berücksichtigen und durch Integration der Masse entlang der Säule den Druck zu berechnen, der in der Tiefe auftritt, die wir schätzen möchten.
ID:(1598, 0)
Charakterisierung der Ozeanschichten
Definition
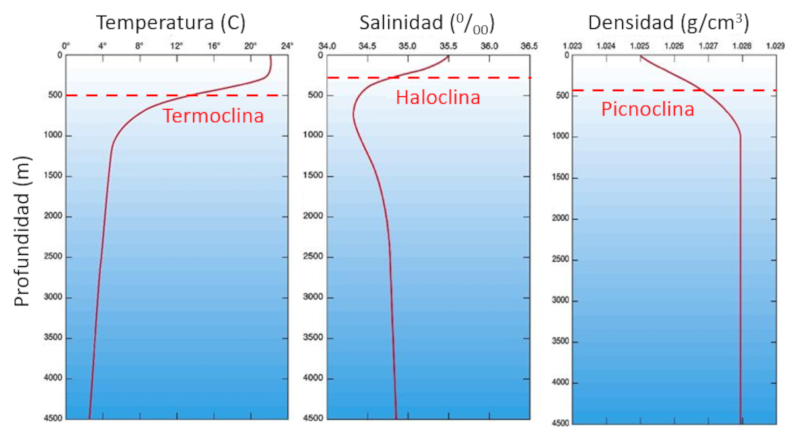
Durch Ekmans Transport verschieben sich die Grenzen zwischen den Oberflächenschichten und den tiefsten Schichten im Ozean. Diese sind durch plötzliche Änderungen der Parameter in Abhängigkeit von der Temperatur gekennzeichnet. Insbesondere gibt es Änderungen in:
• Temperatur (Thermokline)
• Salzgehalt (Halokline)
• Dichte (Pyknokline)
ID:(11684, 0)
Säule mit variabler Dichte
Bild
Um den Druck unter dem Meer in einer bestimmten Tiefe zu berechnen, muss zuerst die Masse eines Volumenelements in einer bestimmten Tiefe geschätzt werden:
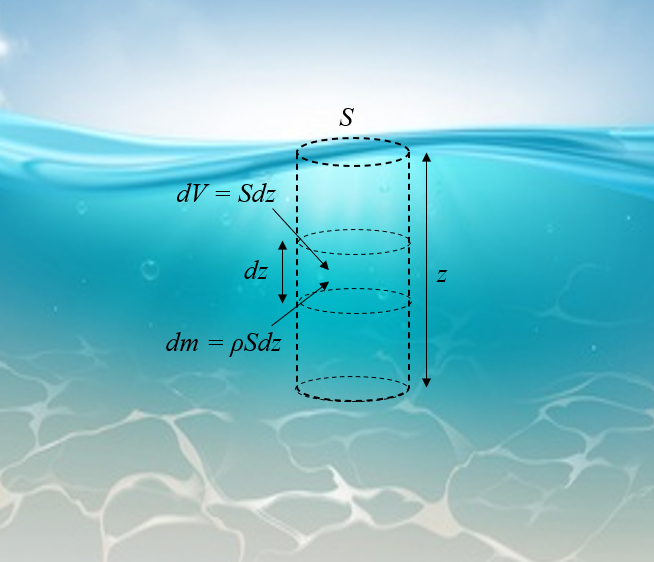
Das Problem in diesem Fall ist, dass die Dichte nicht konstant ist, so dass das typische Verhältnis des Drucks der Wassersäule nicht angewendet werden kann.
ID:(12008, 0)
Dichtemodellierung
Notiz
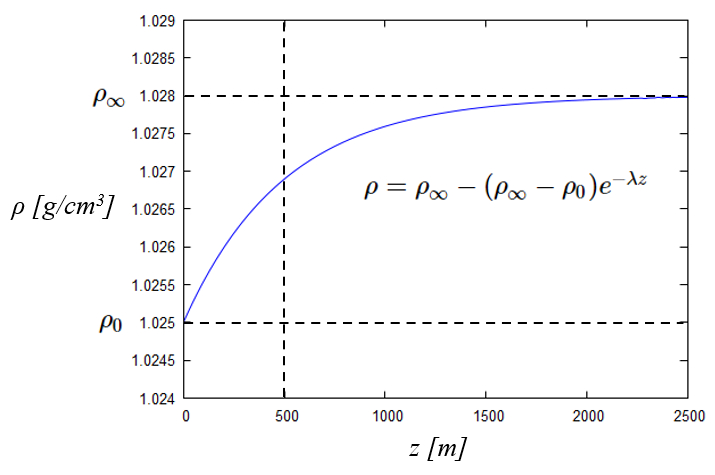
Wenn Sie die Kurve der Dichte des Meerwassers als Funktion der Tiefe betrachten, sehen Sie, dass es die Form eines invertierten Exponentials hat. Mit anderen Worten, der obere Teil kann komprimiert werden und erreicht eine Grenze, bei der das Gewicht der Säule nicht zu einer stärkeren Komprimierung führt:
ID:(12014, 0)
Wassersäule im Meer
Storyboard
Im Falle des Ozeans variiert die Dichte des Wassers in Abhängigkeit von seiner Temperatur und seinem Salzgehalt mit der Tiefe. Aus diesem Grund kann der Druck nicht mit der herkömmlichen Druckformel für die Wassersäule berechnet werden. Es ist notwendig, den Effekt der Dichteschwankung zu berücksichtigen und durch Integration der Masse entlang der Säule den Druck zu berechnen, der in der Tiefe auftritt, die wir schätzen möchten.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
Durch Ekmans Transport verschieben sich die Grenzen zwischen den Oberfl chenschichten und den tiefsten Schichten im Ozean. Diese sind durch pl tzliche nderungen der Parameter in Abh ngigkeit von der Temperatur gekennzeichnet. Insbesondere gibt es nderungen in:
• Temperatur (Thermokline)
• Salzgehalt (Halokline)
• Dichte (Pyknokline)
Ein Wasserelement mit einer H he
Um den Druck unter dem Meer in einer bestimmten Tiefe zu berechnen, muss zuerst die Masse eines Volumenelements in einer bestimmten Tiefe gesch tzt werden:
Das Problem in diesem Fall ist, dass die Dichte nicht konstant ist, so dass das typische Verh ltnis des Drucks der Wassers ule nicht angewendet werden kann.
Con la definici n de la fuerza gravitacional
el aumento de la fuerza en funci n de la masa es
Con la variaci n de la masa
y la variaci n de la fuerza en funci n de la masa
con lo que se obtiene
Con la definici n de la presi n
la presi n aumenta con la fuerza seg n
en donde se asume que la secci n no varia.
Con la definici n de la presi n
el aumento de la fuerza
lleva a un aumento de la presi n
Wenn Sie die Kurve der Dichte des Meerwassers als Funktion der Tiefe betrachten, sehen Sie, dass es die Form eines invertierten Exponentials hat. Mit anderen Worten, der obere Teil kann komprimiert werden und erreicht eine Grenze, bei der das Gewicht der S ule nicht zu einer st rkeren Komprimierung f hrt:
Wenn Sie die Kurve der Dichte mit der Tiefe beobachten k nnen dies mit einem Wert f r die Oberfl chendichte
Con el incremento de la presi n
se puede mediante integraci n calcular la presi n para cualquier profundidad:
Si se emplea la funci n de la densidad
en la ecuaci n de la presi n
se obtiene
ID:(1598, 0)