Flujos de circulación profunda
Storyboard 
Existen varios puntos donde se generan flujos desde la superficie oceánica hacia mayores profundidades, lo que induce una circulación profunda. Esta circulación está sujeta a la fuerza de Coriolis, lo que provoca desviaciones y algunos flujos hacia la superficie (ascenso) que se asocian con las corrientes superficiales.
El modelo clásico para estas corrientes es el de Stommel y Arons, que, aunque simple, explica los diferentes flujos de profundidad observados.
[1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
ID:(1623, 0)
Circulación termohalina
Imagen 
El flujo de agua en las capas más profundas del océano se conoce como circulación termohalina (Termohaline Circulation - THC), ya que su movimiento está asociado con variaciones de temperatura (termo) y salinidad (halina). Para comprender cómo ocurre esto, es necesario describir primero la estructura del sistema.
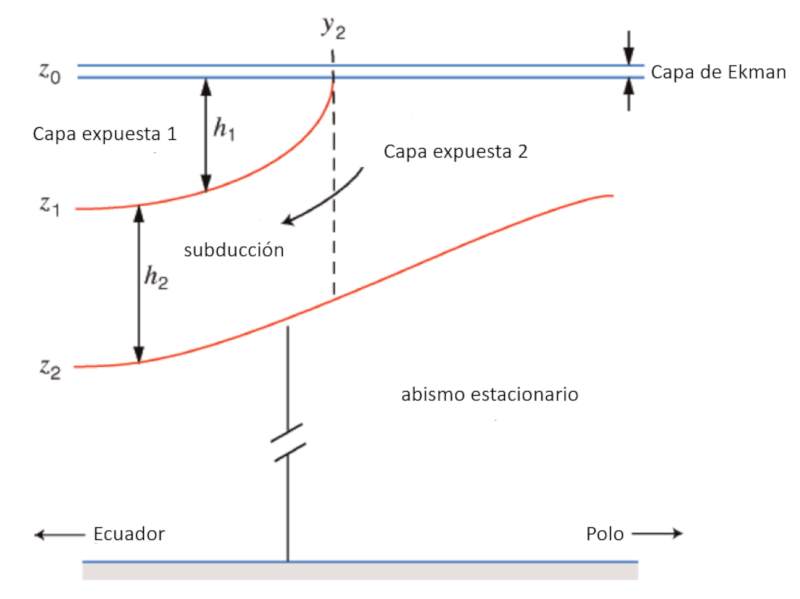
De manera simplificada, el océano se puede modelar como un sistema de tres capas:
- Una capa superior en la cual el movimiento del agua es generado por las corrientes de aire que actúan sobre ella.
- Una capa intermedia cuyo movimiento se genera debido a diferencias de densidad en los océanos, las cuales son causadas por diferencias de temperatura y salinidad (termohalina).
- Una capa profunda que se considera en reposo.
El aumento de la densidad hacia los polos, donde el agua es más fría, provoca que el agua literalmente se hunda, generando una subducción debajo de la capa superficial. El siguiente diagrama resume lo descrito:
ID:(12095, 0)
Circulación termohalina sobre el planeta
Nota 
Si observamos el globo terráqueo, la circulación termohalina se genera cerca de uno de los polos (norte o sur) mediante agua que, debido a su mayor salinidad y menor temperatura, comienza a hundirse. Su flujo se dirige hacia el ecuador, dando lugar a una surgencia que provoca que parte del agua ascienda y fluya en dirección al polo para reemplazar el agua que desciende.
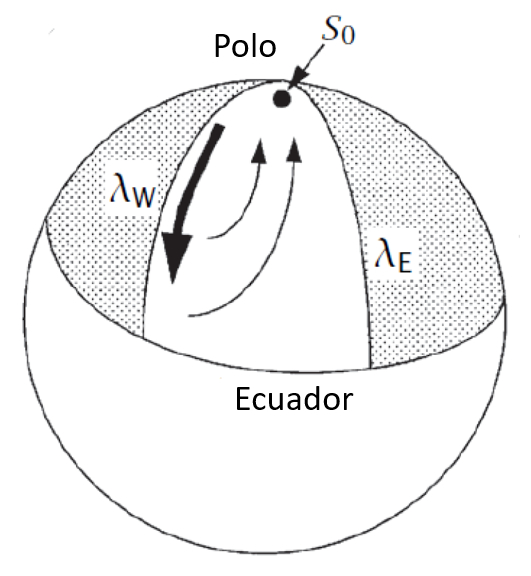
Representación del atlantico norte en el modelo de Stommel y Arons [1], [2]
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulación abisal del océano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulación abisal del océano mundial - II. Un modelo idealizado del patrón y la amplitud de la circulación en cuencas oceánicas.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12096, 0)
Modelo de caja
Cita 
El modelo de Stommel y Arons [1], [2] considera el océano como una caja bidimensional con coordenadas en el eje x e y. En particular:
- Coordenadas en el eje x: $x_w$ (oeste) y $x_e$ (este).
- Coordenadas en el eje y: $y_s$ (sur) y $y_n$ (norte).
Estas coordenadas se representan en el siguiente gráfico:
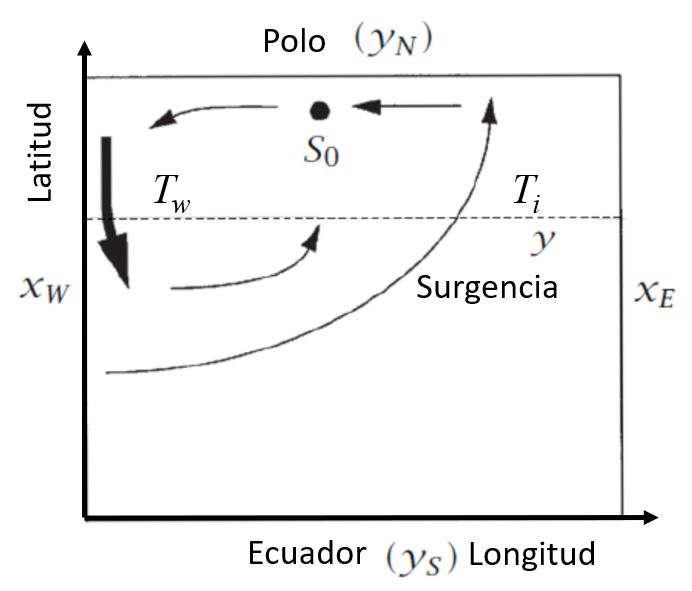
Modelo caja del atlantico [1], [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulación abisal del océano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulación abisal del océano mundial - II. Un modelo idealizado del patrón y la amplitud de la circulación en cuencas oceánicas.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12082, 0)
Tiempos característicos
Ejercicio 
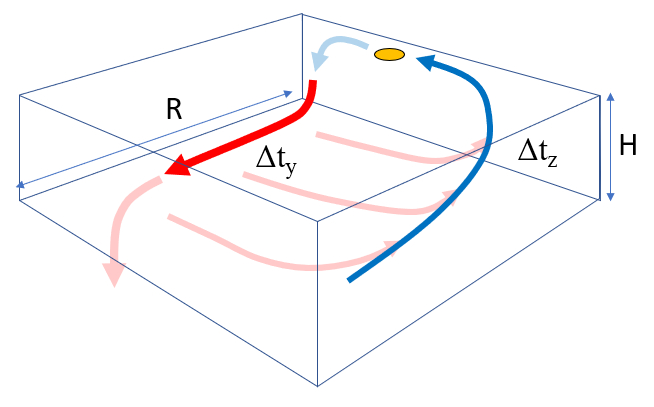
Cada etapa está asociada a un tiempo característico:
- Tiempo de viaje con el flujo principal $\Delta t_y$
- Tiempo de desvío con el flujo de pérdida $\Delta t_x$
- Tiempo de surgencia $\Delta t_z$
ID:(13426, 0)
Velocidades y aceleraciones por flujo
Ecuación 
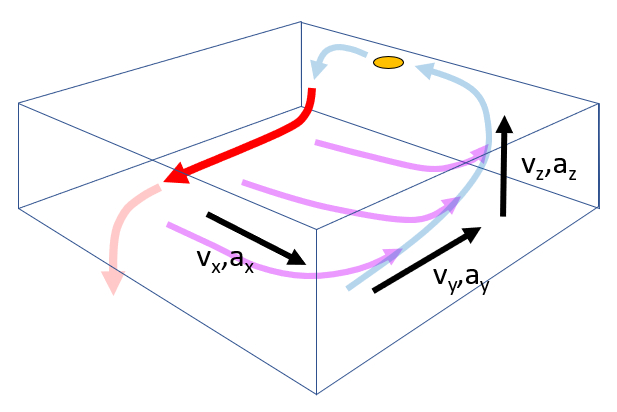
Cada tiempo característico se asocia vía el camino recorrido a las velocidades y aceleraciones:
- Con el flujo principal $v_y, a_y$.
- Con el flujo de pérdida $v_x, a_x$.
- Con la surgencia $v_z, a_z$.
Por lo general, la velocidad inicial (
ID:(13427, 0)
Geometría del flujo de perdida
Script 
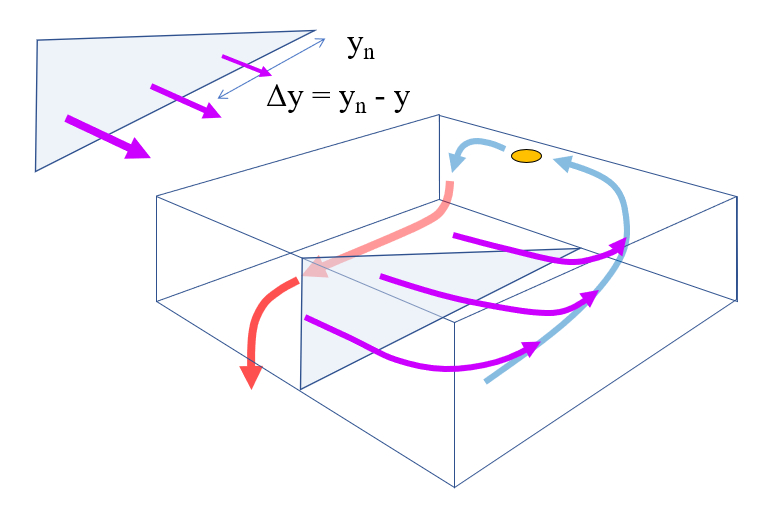
El flujo de pérdida no es uniforme y se distribuye a lo largo de la latitud, por lo que se modela en función de su distancia a la posición más al norte. De esta manera, es nulo en latitudes del norte y máximo en el borde sur del rectángulo donde se modela la circulación:
ID:(13428, 0)
Geometría del flujo de surgencia
Variable 
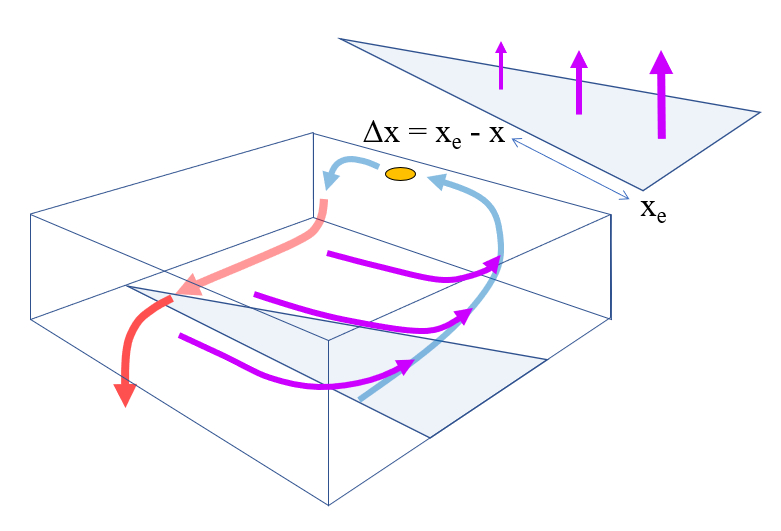
Dado que el flujo de pérdida no es uniforme, la surgencia tampoco lo será. Dentro del mismo modelo, se asume que la surgencia es máxima en el borde este del rectángulo donde se modela la circulación. De manera análoga a la pérdida, se asume una relación lineal:
ID:(13429, 0)
Principales flujos de corrientes profundas
Audio 
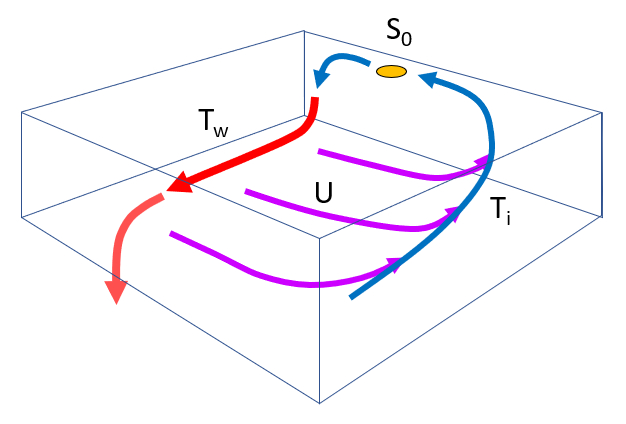
En la modelación del flujo profundo, se deben considerar cuatro flujos:
El flujo principal $F_w$, que se desplaza a lo largo del fondo.
El flujo de pérdida $F_i$, que es la fracción desviada debido a la fuerza de Coriolis.
El flujo de surgencia $U_x$, que corresponde a la fracción de pérdida que alcanza la superficie.
El flujo de hundimiento $S_0$, proveniente de las corrientes superficiales, incluyendo las pérdidas que vuelven a hundirse.
ID:(13425, 0)
Corrientes submarinas y Coriolis
Video 
La denominada Fuerza de Coriolis desempeña un papel esencial en la dinámica del agua en los polos, influenciando cómo las masas de agua descienden debido a las variaciones en temperatura y salinidad.
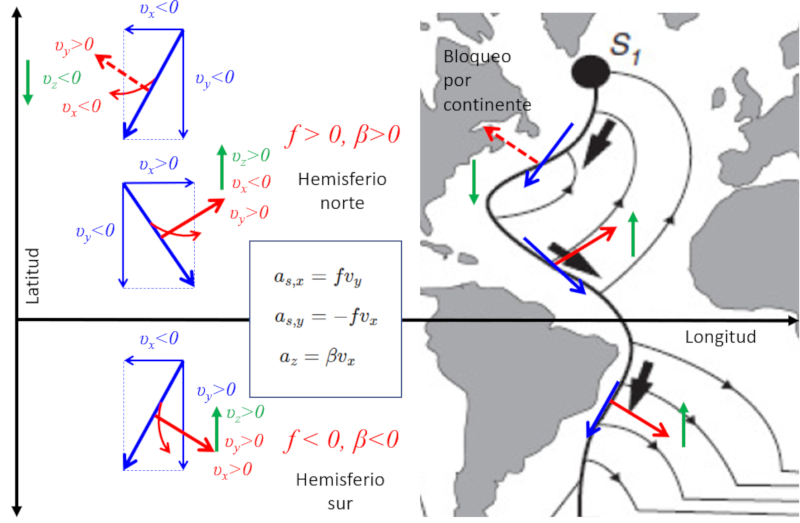
Al analizar el Océano Atlántico, se puede notar un movimiento del agua desde el polo hacia el ecuador, que se desvía hacia el oeste. Este fenómeno es causado por el retraso en relación con la rotación del planeta, al pasar de una zona de menor velocidad a lo largo de la latitud a una de mayor. Este comportamiento se puede modelar mediante la ecuación de Coriolis para la dirección x, que con es
| $ a_{c,x} = f v_y $ |
En esta ecuación, el factor de Coriolis
El contorno geográfico del continente permite un movimiento en la dirección
| $ a_{c,y} = - f v_x $ |
Este cálculo revela que cerca del ecuador se generan desplazamientos que alejan agua de la corriente principal, moviéndola hacia el norte. Si se examina la aceleración en la dirección
| $ a_{cz} = R \beta v_x $ |
ID:(12122, 0)
Flujos de profundidad de Stommel-Arons
Unidad 
Stommel y Arons [1], [2] al final resuelven el modelo indicando los principales flujos de profundidad que existen sobre todo el globo:
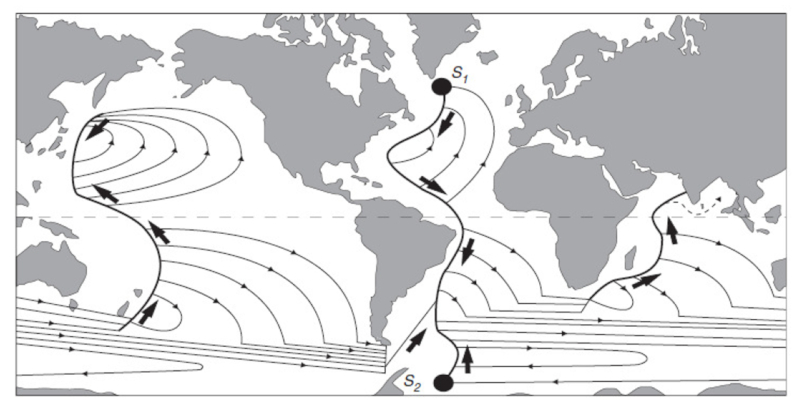
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulación abisal del océano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulación abisal del océano mundial - II. Un modelo idealizado del patrón y la amplitud de la circulación en cuencas oceánicas.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12099, 0)
Estructura del modelo de Stommel-Arons
Code 
Cuando Stommel y Arons [1], [2] establecieron su primer modelo de circulación termohalina, subdividieron los distintos océanos en zonas con surgencia definida (flechas hacia arriba) y con dos fuentes, una en el Ártico y otra en la Antártida:
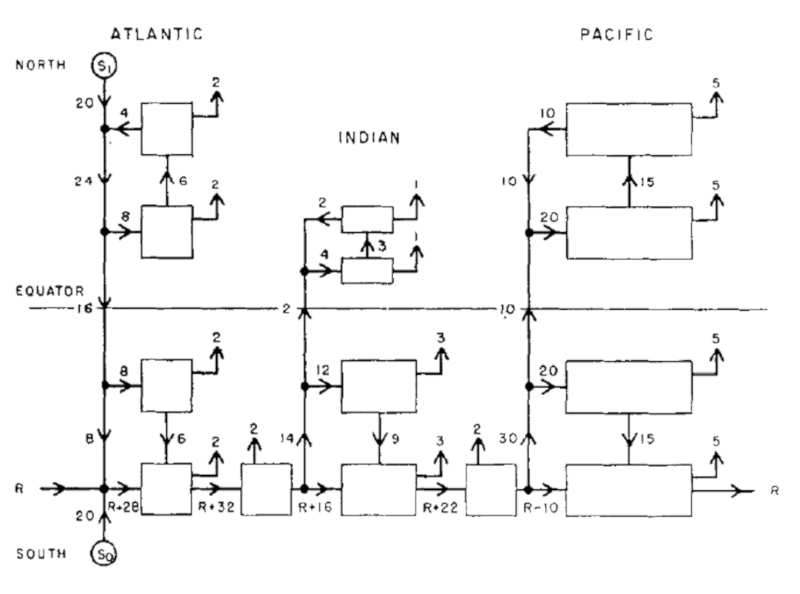
Modelo de circulación a nivel global en Sv (Sverdrup) ($10^6 m^3/s$) [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulación abisal del océano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulación abisal del océano mundial - II. Un modelo idealizado del patrón y la amplitud de la circulación en cuencas oceánicas.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12098, 0)
Circulación termohalina real
Flujo 
Las mediciones han demostrado que la circulación termohalina es un sistema globalmente integrado. Este sistema tiene al menos dos puntos que pueden considerarse como fuentes, y su recorrido se extiende a través de todos los océanos.
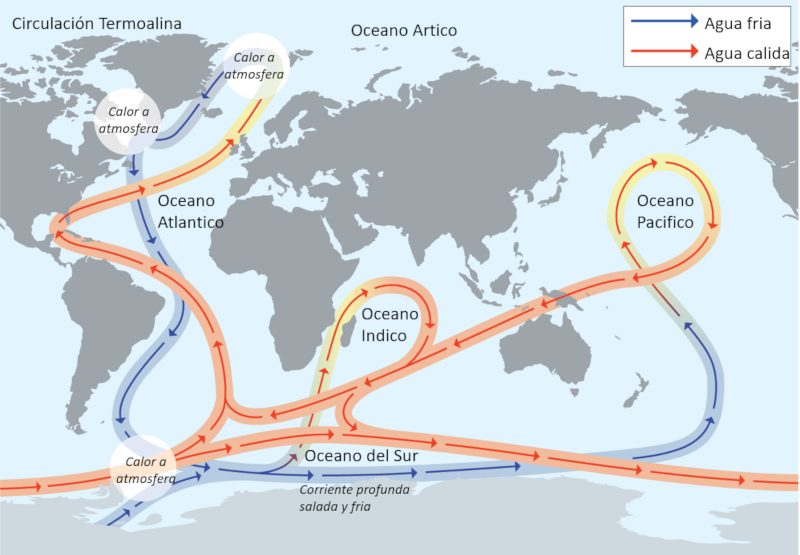
ID:(12097, 0)
Estudio del posible colapso del flujo profundo
Matriz 
A través de múltiples simulaciones se estudian los efectos del deshielo de los casquetes polares en la supresión de los hundimientos y su impacto en la circulación profunda. Existen indicios de que la circulación ha comenzado a reducirse, sin embargo, el colapso de la circulación profunda no implica necesariamente que ocurra lo mismo con la circulación superficial, que es generada por los vientos. Lo que podría suceder es un desplazamiento en la circulación superficial, lo que resultaría en una reducción de la contribución de la Corriente del Golfo de aguas cálidas en el norte de Europa.
A continuación se muestra un diagrama de las variaciones de los flujos en unidades de Sv (Sverdrup), que equivale a $10^6,m^3/s$:
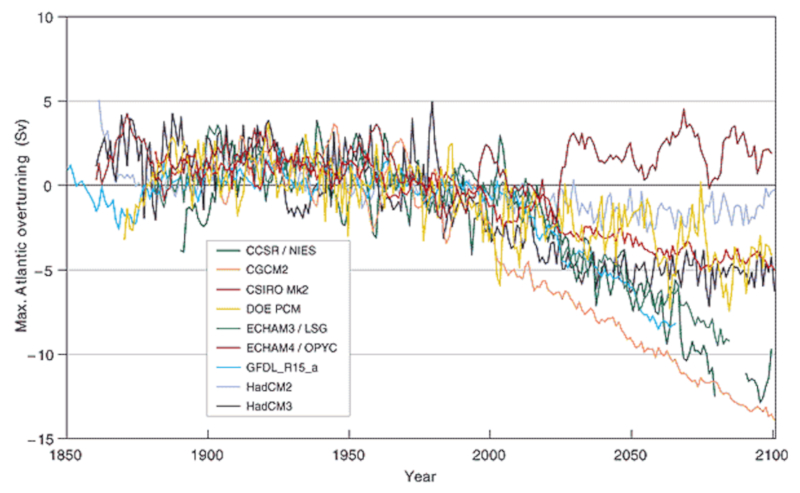
Si asumimos una tasa de hundimiento de aproximadamente 20 Sv, se concluye que en algunas simulaciones se observa la detención de la circulación profunda. Estas variaciones están asociadas a diferentes escenarios futuros de la actividad humana y consideraciones para aspectos en los que se tiene menos certeza sobre su ocurrencia. Para obtener más detalles, se pueden consultar los informes del Panel Intergubernamental sobre Cambio Climático (IPCC).
ID:(13430, 0)
Flujos de circulación profunda
Storyboard 
Existen varios puntos donde se generan flujos desde la superficie oceánica hacia mayores profundidades, lo que induce una circulación profunda. Esta circulación está sujeta a la fuerza de Coriolis, lo que provoca desviaciones y algunos flujos hacia la superficie (ascenso) que se asocian con las corrientes superficiales. El modelo clásico para estas corrientes es el de Stommel y Arons, que, aunque simple, explica los diferentes flujos de profundidad observados. [1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
Variables
Cálculos
Cálculos
Ecuaciones
Como la aceleración de Coriolis en dirección x ($a_{c,x}$) se compone de la velocidad angular del planeta ($\omega$), la latitud ($\varphi$), la velocidad y del objeto ($v_y$) y la velocidad z del objeto ($v_z$):
y la definici n de el factor de Coriolis ($f$) es:
adem s de la restricci n de un movimiento en la superficie en la que:
$v_z = 0$
esto lleva a que la aceleración de Coriolis en dirección x ($a_{c,x}$) sea:
Como la aceleración de Coriolis en dirección y ($a_{c,y}$) se compone de la velocidad angular del planeta ($\omega$), la velocidad x del objeto ($v_x$) y la latitud ($\varphi$):
y la definici n de el factor de Coriolis ($f$) es:
adem s de la restricci n de un movimiento en la superficie en la que:
$v_z = 0$
esto lleva a que la aceleración de Coriolis en dirección y ($a_{c,y}$) sea:
Si introducimos tiempos t picos para cada dimensi n, podemos estimar las aceleraciones de Coriolis $a_i$ como velocidades $v_i$ divididas por sus tiempos t picos $\Delta t_i$, es decir:
$v_i =a_i \Delta t_i$
con $i=x,y,z$. Para la aceleración de Coriolis en dirección z ($a_{c,z}$), con el radio del planeta ($R$), el factor Beta de Coriolis ($\beta$) y la velocidad en paralelo ($v_x$) tenemos que:
Entonces tenemos que la velocidad en surgencia ($v_z$) es el factor Beta de Coriolis ($\beta$), el radio del planeta ($R$), la velocidad en paralelo ($v_x$) y el intervalo de tiempo característico movimiento en $z$ ($\Delta t_z$):
$v_z=\beta R v_x\Delta t_z$
Por otro lado, con la ecuaci n para la componente $y$ de la aceleraci n de Coriolis, se tiene para la aceleración de Coriolis en la superficie, en dirección y ($a_{c,y}$) con el factor de Coriolis ($f$) y la velocidad x del objeto ($v_x$)
por lo que la velocidad y del objeto ($v_y$) con el intervalo de tiempo característico movimiento en $y$ ($\Delta t_y$):
$v_y=a_{s,y}\Delta t_y=- f v_x \Delta t_y$
Reemplazando la velocidad en paralelo ($v_x$) en esta ecuaci n anterior, obtenemos:
Cuando hay un movimiento en la direcci n x (este-oeste), se genera la aceleración de Coriolis en dirección z ($a_{c,z}$) con la velocidad x del objeto ($v_x$), la velocidad angular del planeta ($\omega$) y la latitud ($\varphi$):
Esta situaci n se complementa con la aceleración de Coriolis en la superficie, en dirección x ($a_{c,x}$) (este-oeste), utilizando el factor de Coriolis ($f$) y la velocidad y del objeto ($v_y$):
y la aceleración de Coriolis en la superficie, en dirección y ($a_{c,y}$) (norte-sur) con el factor de Coriolis ($f$) y la velocidad x del objeto ($v_x$), que se define como:
Donde el factor de Coriolis ($f$) est definido como:
As , podemos introducir el factor Beta de Coriolis ($\beta$), definido como:
Obteniendo:
En analog a a el factor de Coriolis ($f$) definido con la latitud ($\varphi$) y la velocidad angular del planeta ($\omega$) como:
el factor var a en el arco $R\theta$, con el radio del planeta ($R$) y la latitud ($\varphi$) como la latitud, seg n:
$\displaystyle\frac{\partial f}{\partial (R\varphi) }=\displaystyle\frac{ 2\omega\cos\varphi }{R}$
por lo que se puede definir el factor Beta de Coriolis ($\beta$) como:
Ejemplos
El flujo de agua en las capas m s profundas del oc ano se conoce como circulaci n termohalina (Termohaline Circulation - THC), ya que su movimiento est asociado con variaciones de temperatura (termo) y salinidad (halina). Para comprender c mo ocurre esto, es necesario describir primero la estructura del sistema.
De manera simplificada, el oc ano se puede modelar como un sistema de tres capas:
- Una capa superior en la cual el movimiento del agua es generado por las corrientes de aire que act an sobre ella.
- Una capa intermedia cuyo movimiento se genera debido a diferencias de densidad en los oc anos, las cuales son causadas por diferencias de temperatura y salinidad (termohalina).
- Una capa profunda que se considera en reposo.
El aumento de la densidad hacia los polos, donde el agua es m s fr a, provoca que el agua literalmente se hunda, generando una subducci n debajo de la capa superficial. El siguiente diagrama resume lo descrito:
Si observamos el globo terr queo, la circulaci n termohalina se genera cerca de uno de los polos (norte o sur) mediante agua que, debido a su mayor salinidad y menor temperatura, comienza a hundirse. Su flujo se dirige hacia el ecuador, dando lugar a una surgencia que provoca que parte del agua ascienda y fluya en direcci n al polo para reemplazar el agua que desciende.
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulaci n abisal del oc ano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulaci n abisal del oc ano mundial - II. Un modelo idealizado del patr n y la amplitud de la circulaci n en cuencas oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
El modelo de Stommel y Arons [1], [2] considera el oc ano como una caja bidimensional con coordenadas en el eje x e y. En particular:
- Coordenadas en el eje x: $x_w$ (oeste) y $x_e$ (este).
- Coordenadas en el eje y: $y_s$ (sur) y $y_n$ (norte).
Estas coordenadas se representan en el siguiente gr fico:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulaci n abisal del oc ano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulaci n abisal del oc ano mundial - II. Un modelo idealizado del patr n y la amplitud de la circulaci n en cuencas oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
Cada etapa est asociada a un tiempo caracter stico:
- Tiempo de viaje con el flujo principal $\Delta t_y$
- Tiempo de desv o con el flujo de p rdida $\Delta t_x$
- Tiempo de surgencia $\Delta t_z$
Cada tiempo caracter stico se asocia v a el camino recorrido a las velocidades y aceleraciones:
- Con el flujo principal $v_y, a_y$.
- Con el flujo de p rdida $v_x, a_x$.
- Con la surgencia $v_z, a_z$.
Por lo general, la velocidad inicial (
El flujo de p rdida no es uniforme y se distribuye a lo largo de la latitud, por lo que se modela en funci n de su distancia a la posici n m s al norte. De esta manera, es nulo en latitudes del norte y m ximo en el borde sur del rect ngulo donde se modela la circulaci n:
Dado que el flujo de p rdida no es uniforme, la surgencia tampoco lo ser . Dentro del mismo modelo, se asume que la surgencia es m xima en el borde este del rect ngulo donde se modela la circulaci n. De manera an loga a la p rdida, se asume una relaci n lineal:
En la modelaci n del flujo profundo, se deben considerar cuatro flujos:
El flujo principal $F_w$, que se desplaza a lo largo del fondo.
El flujo de p rdida $F_i$, que es la fracci n desviada debido a la fuerza de Coriolis.
El flujo de surgencia $U_x$, que corresponde a la fracci n de p rdida que alcanza la superficie.
El flujo de hundimiento $S_0$, proveniente de las corrientes superficiales, incluyendo las p rdidas que vuelven a hundirse.
La denominada Fuerza de Coriolis desempe a un papel esencial en la din mica del agua en los polos, influenciando c mo las masas de agua descienden debido a las variaciones en temperatura y salinidad.
Al analizar el Oc ano Atl ntico, se puede notar un movimiento del agua desde el polo hacia el ecuador, que se desv a hacia el oeste. Este fen meno es causado por el retraso en relaci n con la rotaci n del planeta, al pasar de una zona de menor velocidad a lo largo de la latitud a una de mayor. Este comportamiento se puede modelar mediante la ecuaci n de Coriolis para la direcci n x, que con
En esta ecuaci n, el factor de Coriolis
El contorno geogr fico del continente permite un movimiento en la direcci n
Este c lculo revela que cerca del ecuador se generan desplazamientos que alejan agua de la corriente principal, movi ndola hacia el norte. Si se examina la aceleraci n en la direcci n
Stommel y Arons [1], [2] al final resuelven el modelo indicando los principales flujos de profundidad que existen sobre todo el globo:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulaci n abisal del oc ano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulaci n abisal del oc ano mundial - II. Un modelo idealizado del patr n y la amplitud de la circulaci n en cuencas oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
Cuando Stommel y Arons [1], [2] establecieron su primer modelo de circulaci n termohalina, subdividieron los distintos oc anos en zonas con surgencia definida (flechas hacia arriba) y con dos fuentes, una en el rtico y otra en la Ant rtida:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre la circulaci n abisal del oc ano mundial - I. Patrones de flujo planetario estacionario en una esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre la circulaci n abisal del oc ano mundial - II. Un modelo idealizado del patr n y la amplitud de la circulaci n en cuencas oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
Las mediciones han demostrado que la circulaci n termohalina es un sistema globalmente integrado. Este sistema tiene al menos dos puntos que pueden considerarse como fuentes, y su recorrido se extiende a trav s de todos los oc anos.
A trav s de m ltiples simulaciones se estudian los efectos del deshielo de los casquetes polares en la supresi n de los hundimientos y su impacto en la circulaci n profunda. Existen indicios de que la circulaci n ha comenzado a reducirse, sin embargo, el colapso de la circulaci n profunda no implica necesariamente que ocurra lo mismo con la circulaci n superficial, que es generada por los vientos. Lo que podr a suceder es un desplazamiento en la circulaci n superficial, lo que resultar a en una reducci n de la contribuci n de la Corriente del Golfo de aguas c lidas en el norte de Europa.
A continuaci n se muestra un diagrama de las variaciones de los flujos en unidades de Sv (Sverdrup), que equivale a $10^6,m^3/s$:
Si asumimos una tasa de hundimiento de aproximadamente 20 Sv, se concluye que en algunas simulaciones se observa la detenci n de la circulaci n profunda. Estas variaciones est n asociadas a diferentes escenarios futuros de la actividad humana y consideraciones para aspectos en los que se tiene menos certeza sobre su ocurrencia. Para obtener m s detalles, se pueden consultar los informes del Panel Intergubernamental sobre Cambio Clim tico (IPCC).
Cuando se modela el Atl ntico Norte como una caja con un sistema de coordenadas cercano al ecuador y en la regi n del Caribe, el ancho de la caja se determina restando la posici n oeste de la posici n este:
Al modelar el Atl ntico Norte como una caja con un sistema de coordenadas cercano al ecuador y en la regi n del Caribe, la altura de la caja se calcula restando la posici n sur de la posici n norte:
Siguiendo una analog a con el factor de Coriolis, podemos investigar c mo var a este factor a lo largo del arco, lo cual nos lleva a obtener el factor Beta de Coriolis ($\beta$) dado por la latitud ($\varphi$), el radio del planeta ($R$) y la velocidad angular del planeta ($\omega$) mediante:
Bas ndonos en la relaci n entre la aceleraci n de Coriolis y las velocidades en cada eje, podemos estimar la aceleraci n de la surgencia que se producir en la circulaci n. Utilizando la parametrizaci n que depende del tama o del sector y la latitud de la ubicaci n, obtenemos la aceleración de Coriolis en dirección z ($a_{c,z}$) en funci n de el factor Beta de Coriolis ($\beta$), el radio del planeta ($R$) y la velocidad en paralelo ($v_x$):
Como la aceleración de Coriolis en dirección x ($a_{c,x}$) puede reescribirse con el factor de Coriolis ($f$) y bajo la condici n de que no hay movimiento vertical:
$v_z = 0$
Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección x ($a_{c,x}$) es:
Como la aceleración de Coriolis en dirección x ($a_{c,x}$) puede reescribirse con el factor de Coriolis ($f$) y bajo la condici n de que no hay movimiento vertical:
$v_z = 0$
Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección y ($a_{c,y}$) es:
El movimiento a lo largo de una latitud, debido a la rotaci n de la Tierra, genera una aceleraci n de Coriolis la aceleración de Coriolis en la superficie, en dirección y ($a_{c,y}$), lo que en el intervalo de tiempo característico movimiento en $y$ ($\Delta t_y$) produce la velocidad en meridiano ($v_y$) seg n:
La velocidad de surgencia la velocidad en surgencia ($v_z$) est determinada por la aceleración de Coriolis en dirección z ($a_{c,z}$) en funci n de el intervalo de tiempo característico movimiento en $z$ ($\Delta t_z$):
Para simplificar las ecuaciones, trabajamos con un factor de Coriolis ($f$), que es una constante para el lugar f sico, ya que incluye la velocidad angular del planeta ($\omega$) para la Tierra y la latitud ($\varphi$) para el lugar:
En el hemisferio sur, la latitud es negativa, y con ella 8600, lo que explica que los sistemas roten en direcci n opuesta al hemisferio norte.
La circulaci n del flujo hace que la velocidad en paralelo ($v_x$) tienda a tener una magnitud similar a la velocidad en meridiano ($v_y$) en un giro negativo:
La continuidad del flujo nos permite determinar c mo est n relacionadas las velocidades en cada fase. De esta manera, podemos estimar la velocidad en surgencia ($v_z$) en funci n de el factor Beta de Coriolis ($\beta$), el factor de Coriolis ($f$), el intervalo de tiempo característico movimiento en $y$ ($\Delta t_y$), el intervalo de tiempo característico movimiento en $z$ ($\Delta t_z$), el radio del planeta ($R$) y la velocidad en meridiano ($v_y$):
Como la velocidad de surgencia es con
y la relaci n entre los tiempos debe cumplir con
la velocidad en el fondo es con
La surg ncia depende da velocidade em dire o superf cie e da posi o na caixa. Como maior em dire o ao equador e bastante uniforme ao longo da largura, ela modelada de forma que varia apenas com a dist ncia at a borda norte da caixa:
$y_n - y$
Portanto, com
La velocidad de surgencia se determina utilizando el valor
Se puede modelar el flujo dentro del interior de la caja utilizando la ecuaci n
.
En particular, se observa que la velocidad de surgencia es mayor hacia el borde oeste, lo cual puede ser representado con
La presencia del factor 2 en el modelo es debido a que se est tomando un promedio considerando el gradiente existente.
El tiempo en la direcci n
La conservaci n del flujo implica que el flujo que se desplaza a lo largo de la costa este de Am rica, representado por $T_w$, y las componentes que experimentan surgencia, representadas por $U_x$, son inicialmente generados por el volumen que se hunde, denotado como $S_0$, adem s de aquellos provenientes de la circulaci n a trav s de la surgencia. Por lo tanto, podemos expresarlo de la siguiente manera:
En este caso, existen dos tipos de flujos: el flujo superficial y el flujo hacia o desde la profundidad. Por conservaci n, podemos asumir que el flujo total que fluye hacia las profundidades en el punto S_0 debe ser igual al flujo total generado por la surgencia. Esta ltima ocurre en toda la superficie y con la velocidad vertical, por lo tanto:
Si se multiplica la velocidad con
por la altura
$T_i \sim v_y H \Delta x$
o sea que con
Considerando la ecuaci n de balance, con
la contribuci n de la fuente con
el flujo de fondo
y la surgencia, con
asumiendo que la zona llega al ecuador (
Ya que el factor de Coriolis se define como
puede relacionarse con el factor beta en funci n de su variaci n alrededor de una posici n. Esto se debe a que, en el desarrollo de Taylor, se obtiene:
$f \sim f_0 + \frac{df}{dy}y$
donde la derivada es:
$\frac{df}{dy} = 2\omega\cos\theta = \beta$
Por lo tanto, utilizando
Con
se puede reescribir con
con
ID:(1623, 0)
