Gemessener Wärmeausdehnungskoeffizient
Definition 
Der thermische Ausdehnungskoeffizient für ozeanisches Wasser, wenn er gemessen wird, hat die in der folgenden Grafik dargestellte Form:
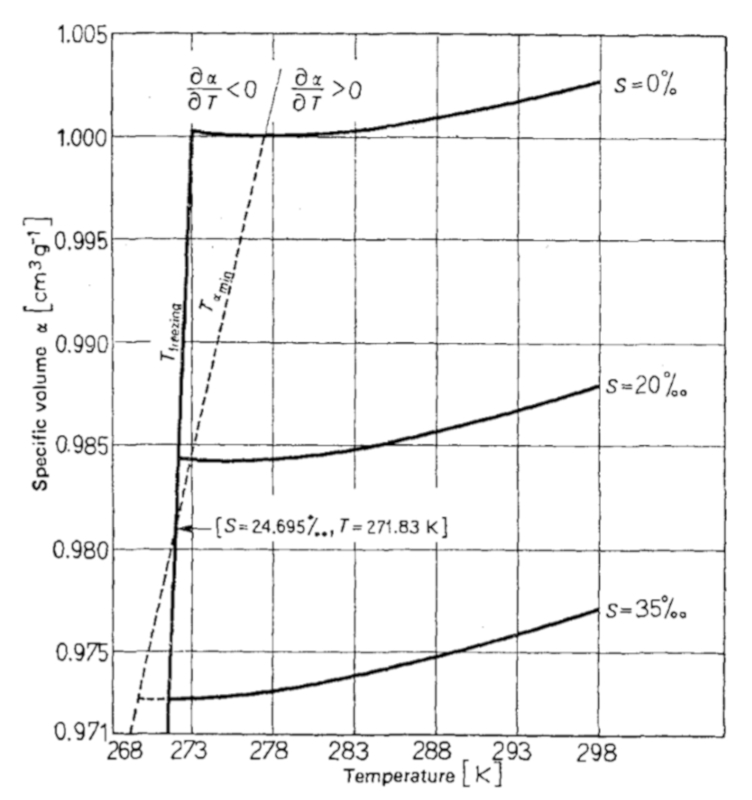
Es ist wichtig zu beachten, dass es, abhängig vom Salzgehalt, einen Bereich gibt, in dem der thermische Ausdehnungskoeffizient negativ ist:
Für einen Salzgehalt von mehr als 24.695 ppt gibt es einen Temperaturbereich, in dem der thermische Ausdehnungskoeffizient negativ ist, was bedeutet, dass sich das Volumen bei steigender Temperatur zusammenzieht.
ID:(11985, 0)
Verursacht eine Vorzeichenänderung des Wärmeausdehnungskoeffizienten
Bild 
Der Grund dafür, dass der thermische Ausdehnungskoeffizient einen Bereich hat, in dem er negativ ist, kann durch die Art und Weise erklärt werden, wie sich Moleküle bei abnehmender Temperatur vor dem Übergang in den festen Zustand neu anordnen. Zwischen 273 K und 277 K bilden Wassermoleküle Ketten, die mehr Volumen benötigen, was erklärt, warum das Volumen bei niedrigeren Temperaturen zunimmt.
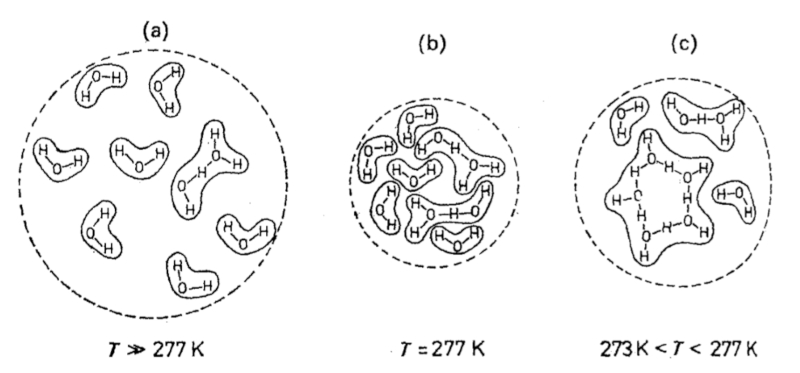
Diese Abbildung veranschaulicht, wie sich Wassermoleküle innerhalb dieses Temperaturbereichs zu Ketten anordnen. Mit abnehmender Temperatur kommen die Moleküle näher zusammen und bilden stabilere Bindungen, was zu einer Volumenexpansion führt. Sobald die Temperatur ausreichend sinkt und das Wasser erstarrt, ordnen sich die Moleküle in eine geordnete kristalline Struktur ein, was zu einer Verringerung des Volumens führt.
Dieses Phänomen wird als "Anomalie des Wassers" bezeichnet und ist eine einzigartige Eigenschaft dieser Verbindung. Die detaillierte Erklärung dieses Verhaltens umfasst Konzepte wie die molekulare Struktur des Wassers und die Bildung von Wasserstoffbrückenbindungen, die entscheidend sind, um zu verstehen, warum der thermische Ausdehnungskoeffizient von Wasser diesen negativen Temperaturbereich aufweist.
Zusammenfassend lässt sich sagen, dass der Bereich, in dem der thermische Ausdehnungskoeffizient von Wasser negativ ist, darauf zurückzuführen ist, dass sich Wassermoleküle bei niedrigen Temperaturen neu anordnen und zu Ketten verbinden, was zu einer Volumenzunahme führt. Diese Erklärung wird durch das Verständnis der molekularen Struktur und der Wasserstoffbrückenbindungen unterstützt, die im Wasser vorhanden sind.
ID:(11986, 0)
Tabelle der Wärmeausdehnungskoeffizienten
Notiz 
Die Koeffizienten der thermischen Ausdehnung in Abhängigkeit von Temperatur und Salinität werden nachstehend aufgelistet:
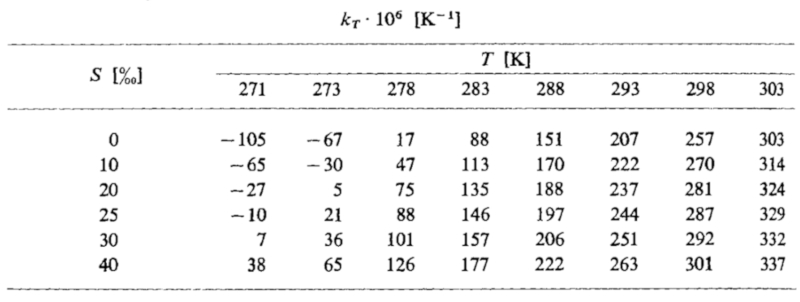
ID:(11987, 0)
Wärmeausdehnung
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
Der thermische Ausdehnungskoeffizient ist definiert durch
| $ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $ |
Im Fall von ozeanischem Wasser arbeiten wir mit dem spezifischen Volumen
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
anstelle des Volumens $V$. Daher kann eine Variablentransformation durchgef hrt werden, wodurch der thermische Ausdehnungskoeffizient wie folgt lautet:
| $ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$ |
.
(ID 11980)
Beispiele
Simulation des Volumenausdehnungsprozesses durch Temperatur. Wenn sich das Wasser erwärmt, vergrößert sich das resultierende Volumen.
(ID 16229)
Der thermische Ausdehnungskoeffizient f r ozeanisches Wasser, wenn er gemessen wird, hat die in der folgenden Grafik dargestellte Form:

Es ist wichtig zu beachten, dass es, abh ngig vom Salzgehalt, einen Bereich gibt, in dem der thermische Ausdehnungskoeffizient negativ ist:
F r einen Salzgehalt von mehr als 24.695 ppt gibt es einen Temperaturbereich, in dem der thermische Ausdehnungskoeffizient negativ ist, was bedeutet, dass sich das Volumen bei steigender Temperatur zusammenzieht.
(ID 11985)
Der Grund daf r, dass der thermische Ausdehnungskoeffizient einen Bereich hat, in dem er negativ ist, kann durch die Art und Weise erkl rt werden, wie sich Molek le bei abnehmender Temperatur vor dem bergang in den festen Zustand neu anordnen. Zwischen 273 K und 277 K bilden Wassermolek le Ketten, die mehr Volumen ben tigen, was erkl rt, warum das Volumen bei niedrigeren Temperaturen zunimmt.

Diese Abbildung veranschaulicht, wie sich Wassermolek le innerhalb dieses Temperaturbereichs zu Ketten anordnen. Mit abnehmender Temperatur kommen die Molek le n her zusammen und bilden stabilere Bindungen, was zu einer Volumenexpansion f hrt. Sobald die Temperatur ausreichend sinkt und das Wasser erstarrt, ordnen sich die Molek le in eine geordnete kristalline Struktur ein, was zu einer Verringerung des Volumens f hrt.
Dieses Ph nomen wird als "Anomalie des Wassers" bezeichnet und ist eine einzigartige Eigenschaft dieser Verbindung. Die detaillierte Erkl rung dieses Verhaltens umfasst Konzepte wie die molekulare Struktur des Wassers und die Bildung von Wasserstoffbr ckenbindungen, die entscheidend sind, um zu verstehen, warum der thermische Ausdehnungskoeffizient von Wasser diesen negativen Temperaturbereich aufweist.
Zusammenfassend l sst sich sagen, dass der Bereich, in dem der thermische Ausdehnungskoeffizient von Wasser negativ ist, darauf zur ckzuf hren ist, dass sich Wassermolek le bei niedrigen Temperaturen neu anordnen und zu Ketten verbinden, was zu einer Volumenzunahme f hrt. Diese Erkl rung wird durch das Verst ndnis der molekularen Struktur und der Wasserstoffbr ckenbindungen unterst tzt, die im Wasser vorhanden sind.
(ID 11986)
Die Koeffizienten der thermischen Ausdehnung in Abh ngigkeit von Temperatur und Salinit t werden nachstehend aufgelistet:

(ID 11987)
Das Problem bei der Arbeit mit dem Volumen im Fall von Meerwasser ist, dass es von den Variationen in Temperatur, Salinit t und Druck abh ngt. Auf der anderen Seite ist die Masse weniger anf llig f r diese Variationen, daher macht es Sinn, mit dem sogenannten spezifischen Volumen zu arbeiten, das durch die Division des Volumens $V$ durch die Masse $M$ berechnet wird:
$\displaystyle\frac{V}{M}$
Allerdings repr sentiert $M/V$ die Dichte, daher wird das spezifische Volumen definiert als:
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
(ID 11984)
Die thermische Ausdehnung, dargestellt durch $\alpha$, kann definiert werden als das Verh ltnis der Volumen nderung $\Delta V/V$ zur Temperaturerh hung $\Delta T$. Mathematisch l sst es sich wie folgt ausdr cken:
| $ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $ |
Das positive Vorzeichen ist mit der Tatsache verbunden, dass eine Temperaturerh hung $\Delta T > 0$ zu einer Volumenexpansion $\Delta V > 0$ f hrt.
(ID 211)
Im Falle des Ozeans wird das Konzept des spezifischen Volumens $\alpha$ anstelle des thermischen Ausdehnungskoeffizienten $k_T$ verwendet. Daher ist es notwendig, den thermischen Ausdehnungskoeffizienten, der normalerweise in Bezug auf die Volumen nderung definiert ist, in Bezug auf die nderung des spezifischen Volumens umzuwandeln. Somit kann f r eine Temperatur nderung $T$ der thermische Ausdehnungskoeffizient in Bezug auf das spezifische Volumen $\alpha$ wie folgt ausgedr ckt werden:
| $ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$ |
(ID 11980)
ID:(1533, 0)
