Utilisateur:
Vitesse du son en mer
Storyboard 
La vitesse du son dans la mer dépend de la pression, de la température et de la salinité.
ID:(1548, 0)
Vitesse du son en mer
Storyboard
La vitesse du son dans la mer dépend de la pression, de la température et de la salinité.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
tant donn que le fréquence des photons ($\nu$) est l'inverse de le période ($T$) :
$\nu=\displaystyle\frac{1}{T}$
cela signifie que a surface de la fontaine ($c$) est gal la distance parcourue en une oscillation, c'est- -dire ERROR:8439, divis e par le temps coul , qui correspond la p riode :
$c=\displaystyle\frac{\lambda}{T}$
En d'autres termes, la relation suivante s'applique :
tant donn que le fréquence des photons ($\nu$) est l'inverse de le période ($T$) :
$\nu=\displaystyle\frac{1}{T}$
cela signifie que a surface de la fontaine ($c$) est gal la distance parcourue en une oscillation, c'est- -dire ERROR:8439, divis e par le temps coul , qui correspond la p riode :
$c=\displaystyle\frac{\lambda}{T}$
En d'autres termes, la relation suivante s'applique :
Exemples
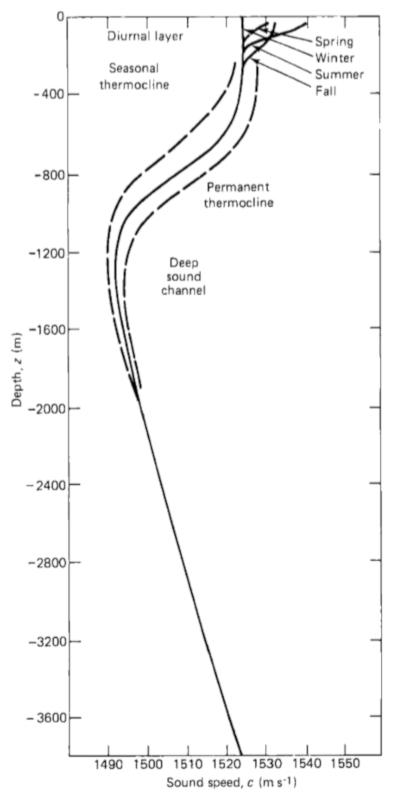
La vitesse du son dans l'oc an varie avec la profondeur, comme le montre le graphiquexa0:
La forme de la courbe peut varier selon la p riode de l'ann e.
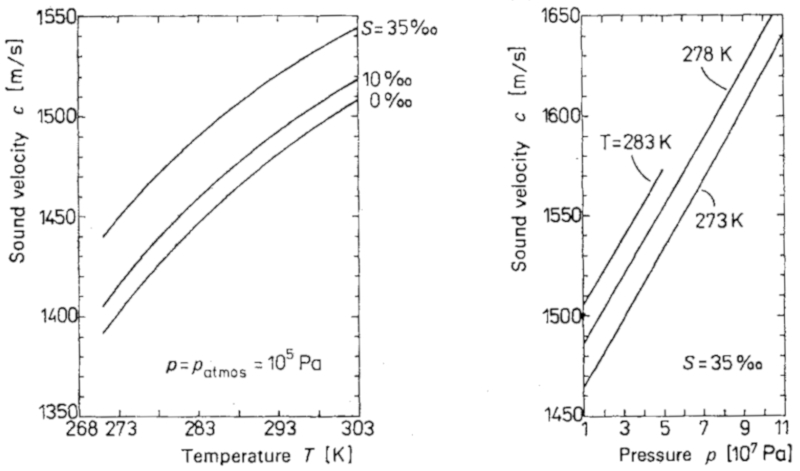
La vitesse du son dans l'oc an d pend de la temp rature et de la pression, comme le montre le graphiquexa0:
En 1977, Clay et Medwin ont d velopp un mod le pour estimer la vitesse du son en fonction de la temp rature, de la salinit et de la pression.
La vitesse du son a vitesse du son ($c$) peut tre estim e en fonction de ERROR:8800, a température ($T$) et a salinité ($s$) l'aide de l'expression suivante :
o $c_i$ sont des constantes empiriques.
R f rence : "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah et Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, novembre 2017.
En 1977, Clay et Medwin ont d velopp un mod le pour estimer la vitesse du son en fonction de la temp rature, de la salinit et de la pression.
La vitesse du son a vitesse du son ($c$) peut tre estim e en fonction de ERROR:8800, a température ($T$) et a salinité ($s$) l'aide de l'expression suivante :
o $c_i$ sont des constantes empiriques.
R f rence : "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah et Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, novembre 2017.
En 1977, Clay et Medwin ont d velopp un mod le pour estimer la vitesse du son en fonction de la temp rature, de la salinit et de la pression.
La vitesse du son a vitesse du son ($c$) peut tre estim e en fonction de ERROR:8800, a température ($T$) et a salinité ($s$) l'aide de l'expression suivante :
o $c_i$ sont des constantes empiriques.
R f rence : "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah et Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, novembre 2017.
Une onde de le fréquence des photons ($\nu$) est li e ERROR:8439 par l'interm diaire de a surface de la fontaine ($c$), selon la formule suivante :
Cette formule correspond la relation en m canique qui tablit que la vitesse dune onde est gale sa longueur donde (distance parcourue) divis e par la p riode doscillation, ou bien directement proportionnelle la fr quence (linverse de la p riode).
Une onde de le fréquence des photons ($\nu$) est li e ERROR:8439 par l'interm diaire de a surface de la fontaine ($c$), selon la formule suivante :
Cette formule correspond la relation en m canique qui tablit que la vitesse dune onde est gale sa longueur donde (distance parcourue) divis e par la p riode doscillation, ou bien directement proportionnelle la fr quence (linverse de la p riode).
ID:(1548, 0)
