Utilisateur:
Sonar
Storyboard 
Un autre usage du son dans l'eau est le sonar, utilisé à la fois comme outil technologique et comme technique employée par les baleines et les dauphins (biosonar) pour déterminer les distances.
Le biosonar est utilisé à la fois pour la navigation et la chasse, en estimant les distances et même les vitesses pour prédire les mouvements futurs de la proie.
ID:(1597, 0)
Sonar
Storyboard
Un autre usage du son dans l'eau est le sonar, utilisé à la fois comme outil technologique et comme technique employée par les baleines et les dauphins (biosonar) pour déterminer les distances. Le biosonar est utilisé à la fois pour la navigation et la chasse, en estimant les distances et même les vitesses pour prédire les mouvements futurs de la proie.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
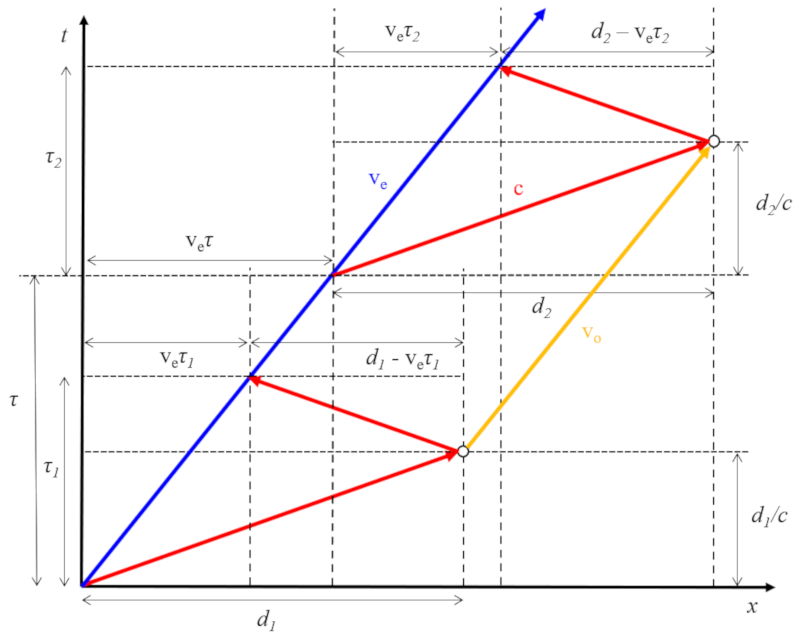
Avec a distance à l'objet lors de l'émission du premier signal ($d_1$) et a vitesse du son ($c$), on peut estimer le moment o le premier signal se refl te comme $d_1/c$, et avec a distance à l'objet lors de l'émission du premier signal ($d_2$), le deuxi me moment comme $\tau + d_2/c$. Ainsi, le temps entre les r flexions des deux signaux est donn par :
$\Delta\tau = \tau + \displaystyle\frac{ d_2 }{ c } - \displaystyle\frac{ d_1 }{ c }$
La position o le premier signal se refl te est a distance à l'objet lors de l'émission du premier signal ($d_1$), et la deuxi me est ERROR:v_e\tau_2 + d_2. Par cons quent, la distance parcourue par le r flecteur est :
$ \Delta x = v_e \tau + d_2 - d_1 $
Ainsi, la vitesse du r flecteur est :
$v_o=\displaystyle\frac{\Delta x}{\Delta t}=\displaystyle\frac{ v_e\tau + d_2 - d_1}{ \tau + \displaystyle\frac{d_2}{c} - \displaystyle\frac{d_1}{c}}$
Comme mentionn pr c demment dans
$d_2-d_1=\displaystyle\frac{1}{2}( c + v_e )( \tau_2 - \tau_1 )$
et la vitesse r sultante est :
Exemples
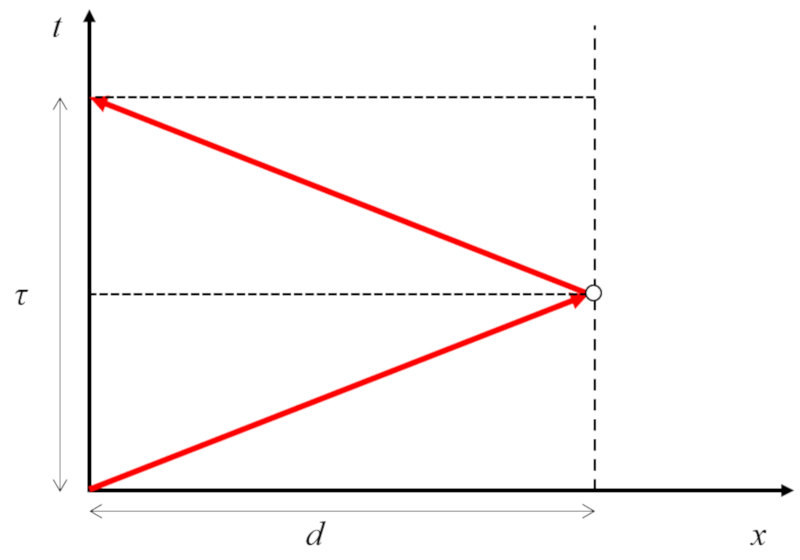
Dans le cas o la fois l' metteur et le r flecteur ne se d placent pas, le trajet parcouru par le son est gal deux fois ERROR:9911 :
Comme le trajet se parcourt a vitesse du son ($c$) en a temps d'écho ($\tau_1$), nous avons que ERROR:9911 est :
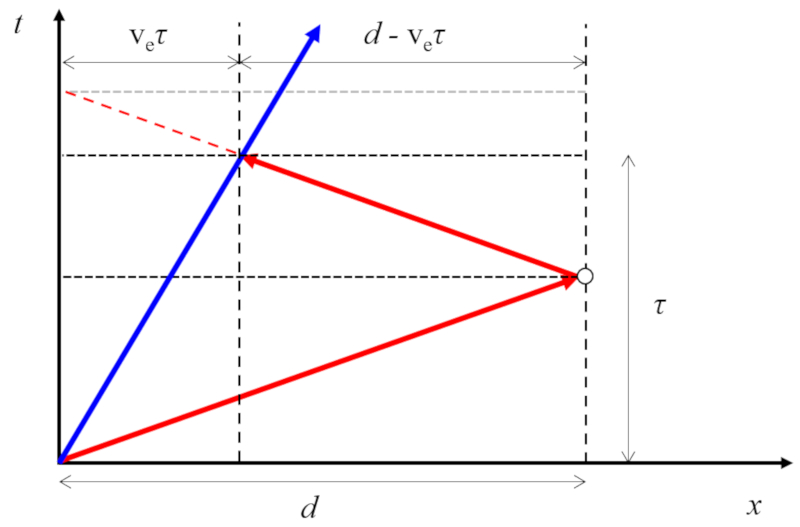
Dans le cas o l' metteur se d place une vitesse a vitesse de l'émetteur ($v_e$) et que le r flecteur est au repos, a vitesse du son ($d_0$) varie en fonction de si le son voyageant a vitesse du son ($c$) n cessite a temps d'écho ($\tau_1$) soit plus grande (si les corps s' loignent) ou plus petite (si les corps se rapprochent) :
Par cons quent, a vitesse du son ($d_0$) est gal
et la position du r flecteur par rapport l' metteur est
en fonction de le temps écoulé depuis le début du suivi ($t$).
Dans le cas o l' metteur se d place une vitesse a vitesse de l'émetteur ($v_e$) et o le r flecteur se d place une vitesse a vitesse du réflecteur ou du récepteur ($v_o$), la distance entre l' metteur et le r flecteur peut tre soit plus grande ($v_e > v_o$) soit plus petite ($v_e < v_o$). Si l'on repr sente cette situation en incluant a temps d'écho ($\tau_1$), le temps du deuxième écho ($\tau_2$) et le temps entre les impulsions ($\tau$), on obtient :
En calculant le chemin parcouru et le temps coul par le r flecteur entre les deux impulsions, on obtient a vitesse du réflecteur ou du récepteur ($v_o$) comme suit :
Connaissant la fois a vitesse de l'émetteur ($v_e$) et a vitesse du réflecteur ou du récepteur ($v_o$), on peut exprimer a position relative de l'émetteur en mouvement et du réflecteur au repos ($x$) en fonction de le temps écoulé depuis le début du suivi ($t$) de la mani re suivante :
avec a vitesse du son ($c$).
En l'absence de mouvement, le temps n cessaire au signal a temps d'écho ($\tau_1$) pour parcourir la distance la vitesse du son a vitesse du son ($c$) est de $c \tau$, soit le double de la distance entre l' metteur et le r flecteur.
Par cons quent, ERROR:9911 est :
Dans le cas o l' metteur se d place une vitesse de a vitesse de l'émetteur ($v_e$) et que le r flecteur reste immobile, sa distance initiale a vitesse du son ($d_0$) peut tre estim e en utilisant le temps d' cho a temps d'écho ($\tau_1$). Dans ce sc nario, la distance parcourue est gale $c \tau_1$, qui est gal la distance initiale entre l' metteur et le r flecteur a vitesse du son ($d_0$), plus le retour, qui est le m me $d_0$ moins la distance parcourue par l' metteur $v_e\tau_1$. Ainsi, nous avons :
$d_0 + d_0 - v_e\tau_1 = c\tau_1$
ou que a vitesse du son ($d_0$) est :
Pour d terminer a position relative de l'émetteur en mouvement et du réflecteur au repos ($x$), il faut consid rer a vitesse du son ($d_0$) et soustraire le chemin parcouru par l' metteur. Ce dernier est calcul partir de a vitesse de l'émetteur ($v_e$) et le temps écoulé depuis le début du suivi ($t$), ce qui donne :
A vitesse du réflecteur ou du récepteur ($v_o$) peut tre calcul partir de a vitesse de l'émetteur ($v_e$) et a vitesse du son ($c$), ainsi que a temps d'écho ($\tau_1$), le temps du deuxième écho ($\tau_2$) et le temps entre les impulsions ($\tau$), en utilisant la formule suivante :
ID:(1597, 0)
