Usuario:
Intercambio de momento
Storyboard 
El intercambio de momento entre la atmósfera y el océano se refiere al proceso mediante el cual la atmósfera impulsa al océano, generando las correspondientes corrientes marinas.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1631, 0)
Tensión en superficie
Descripción
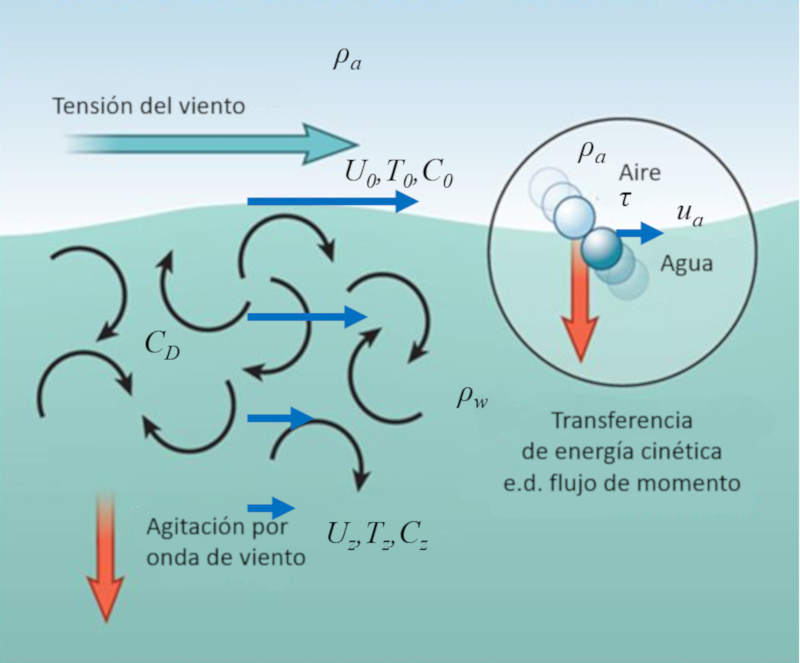
El viento sobre la superficie del océano está compuesto por un gran número de moléculas que golpean periódicamente las moléculas del agua en la superficie.
De esta manera, parte de la energía cinética de las moléculas del aire se transfiere a las moléculas del agua, lo que puede representarse como una tensión que el aire ejerce sobre el agua.
El efecto resultante es la creación de remolinos superficiales que, a su vez, afectan a capas más profundas, transmitiendo la velocidad del viento a una capa superficial del océano. De esta manera, la energía del viento se transfiere a una capa cercana a la superficie del océano, aumentando la velocidad del agua en esa zona.
ID:(12303, 0)
Esquema general de tipos de perturbaciones
Imagen
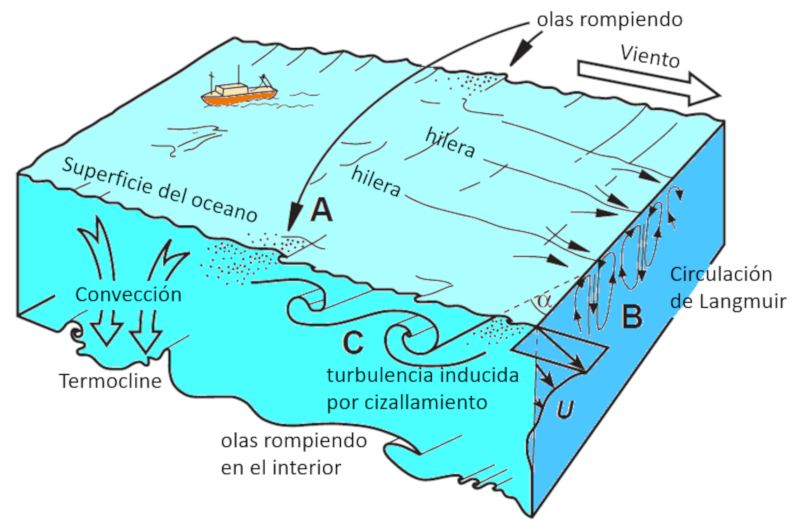
En general, al observar el océano, se pueden identificar diversos mecanismos que generan vórtices y turbulencias, contribuyendo así a los procesos de mezcla.
Dentro de la capa superficial, destacan:
• Las olas superficiales generadas por los vientos.
• La circulación de Langmuir, que forma hileras visibles desde el aire en la superficie.
• El rompimiento de olas superficiales.
Mientras que entre el borde inferior de la capa de mezcla y la termoclina, se destacan:
• Turbulencias por cizallamiento en el borde superior.
• Ondas internas rompiendo en el borde inferior.
• Convección.
• Inestabilidades verticales.
Estos fenómenos se representan en el siguiente diagrama:
ID:(12180, 0)
Ondas estables de Langmuir
Descripción
Uno de los fenómenos que surge de las corrientes superficiales inducidas por el viento es la conocida circulación de Langmuir:
The instability of the ocean to Langmuir circulations, S. Leibovich and S. Paoluccit, J. Fluid Mech. (1981). vol. 102, pp. 141-167
Este fenómeno se origina de manera similar al transporte de Ekman, donde debido a la fuerza de Coriolis se forman zonas de hundimiento que generan remolinos ascendentes. La circulación se completa con la formación de una zona de surgencia:
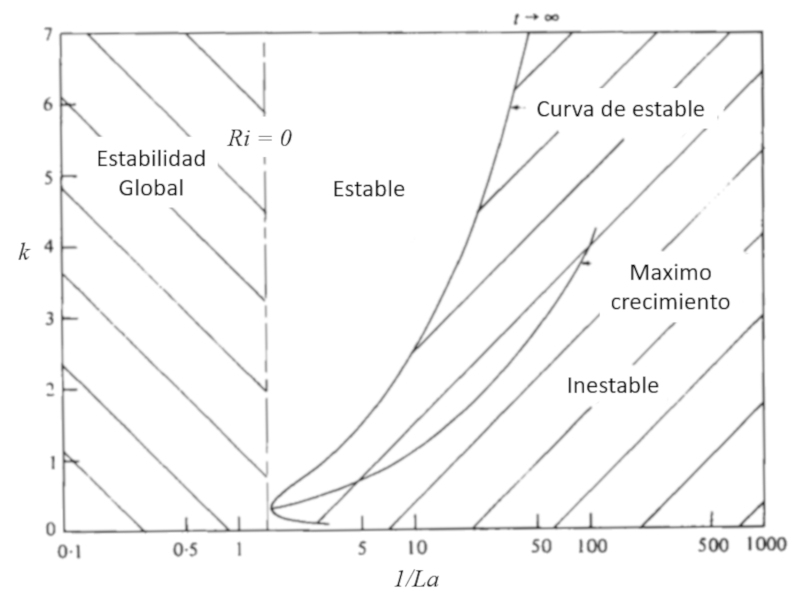
En el artículo mencionado en la próxima imagen se llega a la conclusión de que existen condiciones específicas para la formación de la circulación de Langmuir, las cuales dependen de diversas variables y de la propia oscilación:
ID:(12221, 0)
Modelo
Top
Cálculos
Variables
Parámetros
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar Ecuación
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$
La = sqrt( u_a / u_w )
$ \tau = \tau_t + \tau_w + \tau_{\eta} $
tau = tau_t + tau_w + tau_eta
$ \tau_t = \rho_a C_D ( u_a - u_w )^2$
tau_t = rho_a * C_D * ( u_a - u_w )^2
$ \tau_t = \rho_a u_a ^2 $
tau_t = rho_a * u_a ^2
$ \displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$
u_a ^2/ u_w ^2 = rho_w / rho_a
ID:(15643, 0)
Perfil de velocidad en la capa superficial (MOST)
Ecuación
La fuerza el tensión del viento ($\tau_t$) ejercida sobre la superficie puede modelarse según la teoría de similaridad de Monin-Obukhov (MOST) como la transferencia de energía cinética del aire a la capa superior del océano.
Para ello, se asume que el tensión del viento ($\tau_t$) es proporcional a el densidad del aire ($\rho_a$) y a la diferencia al cuadrado entre el velocidad del aire ($u_a$) y el velocidad del agua ($u_w$). La proporcionalidad se considera mediante la introducción de el constante de arrastre ($C_D$), lo que lleva a la conclusión de que:
| $ \tau_t = \rho_a C_D ( u_a - u_w )^2$ |
ID:(12222, 0)
Tensión en la superficie (MOST)
Ecuación
El modelo de Teoría de Similitud de Monin-Obukhov (MOST) modela la tensión superficial, que es proporcional al cuadrado de el velocidad del aire ($u_a$) en la superficie y a el densidad del aire ($\rho_a$).
En este caso, la fracción superficial se estima mediante la densidad de la energía cinética, que se correlaciona con la tensión superficial.
Por lo tanto, se estima que el velocidad del aire ($u_a$) es
| $ \tau_t = \rho_a u_a ^2 $ |
ID:(12220, 0)
Tensión total en la interfase
Ecuación
La variable el tensión superficial aire-agua ($\tau$) incluye el tensión del viento ($\tau_t$), el tensión de las olas ($\tau_w$), y el tensión de la viscosidad ($\tau_{\eta}$). Por consiguiente, puede expresarse como:
| $ \tau = \tau_t + \tau_w + \tau_{\eta} $ |
ID:(12232, 0)
Relación entre velocidades
Ecuación
Si suponemos una transición continua en la densidad de energía en la interfaz entre el aire y el agua, y consideramos que esta energía es de naturaleza cinética, entonces con el densidad del aire ($\rho_a$), el velocidad del aire ($u_a$) y el densidad del agua ($\rho_w$), el velocidad del agua ($u_w$), podemos establecer la siguiente relación:
$\rho_a u_a^2=\rho_w u_w^2$
Por lo tanto, podemos establecer la relación:
| $ \displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$ |
Además, podemos considerar que la densidad de energía tiene la misma unidad que la tensión superficial, lo que explica la igualdad, ya que en un sistema en equilibrio, las tensiones deben ser iguales.
ID:(12234, 0)
Número de Langmuir
Ecuación
La relación entre el velocidad del aire ($u_a$) y el velocidad del agua ($u_w$) se estudia a través de el numero de Langmuir ($La$). Por lo tanto, el número de Langmuir se puede definir como la proporción de la raíz cuadrada de ambas velocidades:
| $ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$ |
ID:(12219, 0)
Intercambio de CO2, velocidad desde el aire
Ecuación
La velocidad de transferencia del gas en el agua ($k_w$) del gas se describe en función de el velocidad del agua ($u_w$), el velocidad del aire ($u_a$), el número de Schmidt ($Sc$), el factor beta del transporte aire a agua de CO2 ($\beta$) y exponente de Schmidt ($n$) de la siguiente manera:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)