mechanisms

La radiaci n puede ser absorbida y reflejada en interfaces entre dos medios (en este caso aire y nubes/suelo). La intensidad incidente ($I_s$) se refleja en funci n de el albedo ($a$) resultando la intensidad reflejada ($I_r$) seg n:

equation=9987

Por otro lado existe una componente la intensidad absorbida ($I_a$) que es el complemento de la intensidad reflejada ($I_r$) seg n:

equation=10325

Esto se puede repressentar en forma grafica como se ve a continuaci n:

image

Los albedos seg n el tipo de superficie son:

Fuente: Effects of Implementing MODIS Land Cover and Albedo in MM5 at Two Contrasting U.S. Regions, Ismail Yucel, American Meteorological Society, 2006, October, page 1043

La clasificaci n est definida en (MODIS Land Cover and Land-Cover Change)

En general, la luz puede interactuar con el medio a trav s del cual se propaga.

Para modelar esta interacci n, se puede introducir una probabilidad de que ocurra dicha interacci n.

En este sentido, habr una fracci n de luz que interact a y el complemento que contin a propag ndose sin interactuar.

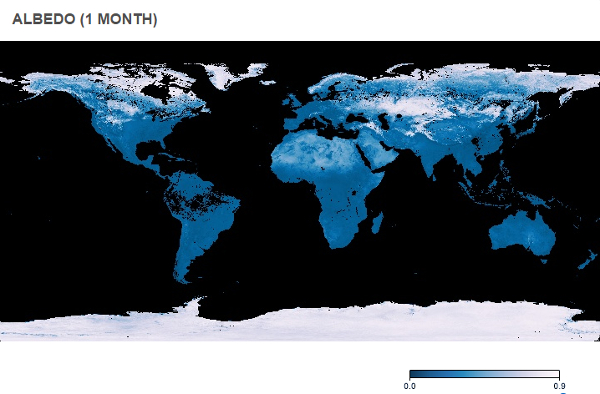
El albedo de un cuerpo indica la fracci n de radiaci n que es reflejada. Aunque esta es una funci n de la frecuencia de la luz, se puede considerar que la variaci n es menor dentro de un tipo de radiaci n. En este caso, nos interesa principalmente c mo se refleja la luz visible. En el caso de la Tierra, esto es:

image

La NASA, a trav s de su Observatorio de la Tierra, permite estudiar la distribuci n mensual e incluso diaria del albedo de la superficie en su p gina:

NASA Earth Observatory - Albedo

Las diferentes reas se pueden identificar utilizando la clasificaci n de la p gina:

NASA Earth Observatory - Land Cover

para establecer el albedo promedio t pico por tipo de rea (el albedo puede fluctuar durante el a o).

Uno de los par metros que no es medido directamente por los sat lites es el albedo atmosf rico. Sin embargo, este se relaciona con la radiaci n de manera similar al grosor ptico de la atm sfera, como se indica en la siguiente gr fica:

image

Por ello, se puede inferir un comportamiento del albedo $a_a$ del tipo:

$a_a \sim 1 - e^{-\delta/\delta_0}$

donde $\delta$ es el grosor ptico y $\delta_0$ es un grosor caracter stico de aproximadamente 55 [-].

El albedo resulta algo mayor que el valor estimado por las mediciones de flujos, mostrando que se mantiene constante en el tiempo no existiendo una explicaci n clara para el nico valor que diverge:

php

La marcada estacionalidad se puede deber a las nieves en invierno en el hemisferio norte que aumentan el albedo en forma sustancial.

Para estimar el albedo, se puede considerar el grosor ptico de la atm sfera, que tiende a ser mayor en la segunda mitad del a o y ha mostrado una leve tendencia a la baja en los ltimos a os:

php

La marcada estacionalidad puede deberse a las nevadas en el invierno del hemisferio norte, que aumentan el albedo de manera sustancial.

Si se promedia el albedo por latitud se obtiene una curva de la forma:

php

Resaltan los altos albedos en los extremos que corresponden a la alta reflexi n debido a los hieles de la ant rtica y del rtico siendo estos ltimos menores por los deshielo de verano. El menor valor promedio en el hemisferio sur radica de la mayor superficie de oc anos que existe en comparaci n con el hemisferio sur. La baja a cero en el hemisferio sur corresponde a una falta de mediciones ya que en esta zona solo hay oc ano y solo un periodo veraniego con luz solar.

Si se promedia el grosor ptico por latitud, se obtiene una curva con la siguiente forma:

php

Destacan altos grosores pticos en los extremos, que corresponden a la alta reflexi n debido a los hielos de la Ant rtida y del rtico, siendo estos ltimos menores por el deshielo de verano. El menor valor promedio en el hemisferio sur se debe a la mayor superficie de oc anos en comparaci n con el hemisferio norte. La baja a cero en el hemisferio sur corresponde a una falta de mediciones, ya que en esta zona solo hay oc ano y solo un periodo veraniego con luz solar.

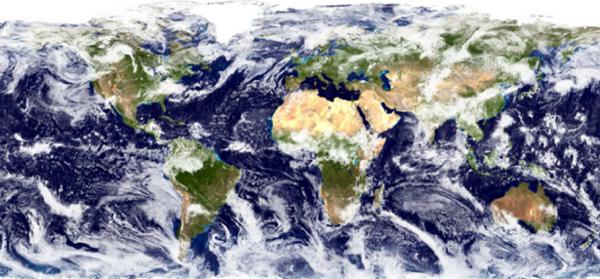
En promedio, las nubes cubren m s del 40% de la superficie de la Tierra:

image

Dado que son visibles, las nubes reflejan la luz, lo que se traduce en radiaci n visible y est relacionado con el albedo atmosf rico.

La cobertura muestra valores promedios mayores a los que se obtiene de los modelos. Ademas muestra una leve tendencia al aumento que puede corresponder a efectos del cambio clim tico de aumento de agua en la atm sfera:

php

La estacionalidad corresponde a los periodos de verano/invierno en que se concentran las temperadas de lluvias.

Si se promedia la fracci n de cobertura de las nubes seg n la latitud se obtiene la siguiente distribuci n:

php

Se observa que existe un m ximo central que corresponde a la convecci n ecuatorial. Luego se observan dos m nimos en las latitudes en torno a los borde de las celdas de Hardley ambos hemisferios. Finalmente baja nuevamente hacia la celda polar.

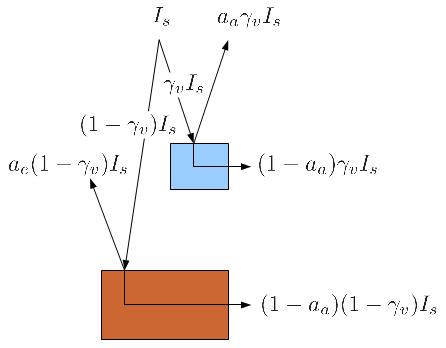
De la intensidad media de la tierra ($I_p$), una fracci n igual a la cobertura de atmósfera para radiación VIS ($\gamma_v$),

$\gamma_v I_p$

interact a con la atm sfera, mientras que el resto,

$(1-\gamma_v) I_p$

llega a la superficie terrestre. La cobertura de atmósfera para radiación VIS ($\gamma_v$) representa la proporci n de la superficie que est cubierta por nubes.

En el caso de la atm sfera, el albedo de la atmósfera de la tierra ($a_a$) determina la absorci n y la reflexi n. De la fracci n que interact a con la atm sfera, una fracci n,

$a_a \gamma_v I_p$

es reflejada, mientras que,

$(1-a_a) \gamma_v I_p$

es absorbida.

En el caso del planeta, el albedo de la superficie del planeta ($a_e$) determina la absorci n y la reflexi n. De la fracci n que llega al planeta, una fracci n,

$a_e (1-\gamma_v) I_p$

es reflejada, mientras que,

$(1-a_e) (1-\gamma_v) I_p$

es absorbida.

image

De la radiaci n solar la intensidad media de la tierra ($I_p$) incidente, una fracci n la cobertura de atmósfera para radiación VIS ($\gamma_v$) interact a con la nube que absorbe una intensidad VIS que interactua con las atmósfera ($I_{sav}$), calcul ndose de la siguiente manera:

equation=9986

Si consideramos los valores del modelo D1+0, la radiaci n solar es del orden de:

$I_s \sim 342 W/m^2$

y un total de:

$I_{sav} \sim 157 W/m^2$

interact a con la atm sfera, lo que significa que la cobertura visible es del orden de:

$\gamma_v \sim 0.46$

.

La intensidad VIS reflejadas por la atmósfera ($I_{asv}$) se calcula utilizando el albedo de la atmósfera de la tierra ($a_a$) y la intensidad VIS que interactua con las atmósfera ($I_{sav}$) mediante:

equation=9987,1

Reflejando en un modelo D1+0,

$I_{asv} \sim 79 W/m^2$

del total de

$\gamma_v I_s \sim 157 W/m^2$

que interact a con la atm sfera, se concluye que el albedo de esta debe ser del orden de

$a_a \sim 0.503$

.

La intensidad VIS absorbida por la atmósfera ($I_{sa}$) se calcula utilizando el albedo de la atmósfera de la tierra ($a_a$) y la intensidad VIS que interactua con las atmósfera ($I_{sav}$) mediante:

equation=10325,2

En un modelo D1+0, esto corresponde a:

$I_{sa} \sim 78 W/m^2$

lo que equivale al 22.8% de la radiaci n incidente.

De la intensidad media de la tierra ($I_p$), solo una fracci n llega a la superficie de la Tierra. El factor que lo determina es la cobertura de atmósfera para radiación VIS ($\gamma_v$), por lo que la intensidad VIS que llega a la superficie de la tierra ($I_{sev}$) se expresa como:

equation=10324

Con una intensidad solar de

$I_s \sim 342 W/m^2$

y una cobertura atmosf rica de

$\gamma_v \sim 0.459$

la radiaci n que alcanza la superficie de la Tierra es:

$I_{sev} \sim 185 W/m^2$

Esto corresponde al 54.1% de la radiaci n solar. Esta radiaci n, que tiene en cuenta la p rdida de intensidad debido a la cobertura atmosf rica, es lo que se conoce como insolaci n solar.

La insolaci n terrestre muestra valores algo mas altos que lo que se estima con el modelo. Por otro lado se observa un incremento importante desde el 2010 cuyo origen no queda bien claro:

php

Cabe mencionar que en el 2010 las manchas solares pasaron por un m nimo y en 2017 ya se sobrepaso el m ximo que se asocia a un incremento de la radiaci n solar. Sin embargo el efecto es menor (menos de 0.1%) por lo que no explicar a la magnitud del incremento.

Por otro lado se observa un efecto estacionalidad que marca un valor mayor para el inicio del a o.

La insolaci n en la tierra es la radiaci n visible (onda larga) que llega a la superficie de la tierra. El promedio general, en tiempo y posici n en la tierra, es de 184,W/m^2 (modelo tipo D0). Sin embargo, si se observa diferenciando la latitud se obtiene una distribuci n como se muestra a continuaci n:

php

Esta curva muestra que la intensidad en el ecuador es m xima superando los 260,W/m^2 y m nima hacia los polos en donde llega a un nivel entre 110-120,W/m^2. La baja general hacia los polis se debe al angulo de incidencia. La falta de simetr a entre ambos hemisferios se debe a la in-homogeneidad en la distribuci n de tierra firma y con ello la formaci n de nubes que reduce la insolaci n.

En un modelo D1+0, la radiaci n que llega a la superficie terrestre se estima en:

$I_{sev} \sim 184 W/m^2$

De esta cantidad, una fracci n aproximada de:

$I_{esv} \sim 23 W/m^2$

es reflejada de vuelta al espacio. Por lo tanto, se puede concluir que el albedo de la superficie terrestre debe ser del orden de:

$a_e \sim 0.125$

Este valor est influenciado por el bajo albedo de los oc anos (0.06), los cuales cubren aproximadamente el 72% del planeta.

De la intensidad VIS que llega a la superficie de la tierra ($I_{sev}$), una fracci n proporcional a el albedo de la superficie del planeta ($a_e$) es reflejada, mientras que el complemento es absorbido por la Tierra. Por lo tanto, la intensidad VIS absorbida por la tierra ($I_{ev}$) se calcula como:

equation=10325,1

Con un albedo de

$a_e \sim 0.125$

y una radiaci n solar incidente de

$I_{sev} \sim 184 W/m^2$

se obtiene que:

$I_{ev} \sim 161 W/m^2$

es la cantidad de radiaci n solar absorbida por la Tierra. Esto corresponde al 87.5% de la radiaci n solar incidente.

La reflexi n de onda corta corresponde a la suma de lo que refleja la atm sfera (unos 79 W/m2) y la superficie de la tierra (unos 23 W/m2) lo que corresponde unos 102 W/m2 lo que es algo superior a los 97 W/m2 que indican las estimaciones.

php

En la curva estacional se observan valores sobre el valor esperado alrededor del inicio del a o lo que podr a corresponder al incremento del albedo por efecto de nieve en el hemisferio norte.

La reflexi n en onda corta (luz visible) se origina tanto en la superficie como en las nubes. Al ser la primera solo del orden de 23,W/m^2 y la segunda del orden de 169,W/m^2 dominara en la zona de alta radiaci n solar el efecto de la atm sfera. Por ello se observa en la distribuci n de radiaci n de onda corta en funci n de la latitud:

php

una baja en las zonas aleda as al ecuador. Esto es en las zonas en las celdas de Hardley en que existe una baja cobertura y por ello una menor reflexi n. Esto cambia hacia los polos en que la radiaci n en si disminuye al igual que la cobertura pero aumenta dram ticamente el albedo y con ello la reflexi n por parte del hielo de las capas polares.

model

La intensidad transmitida ($I_t$) es igual a la intensidad incidente ($I_s$) disminuido por ERROR:8393, de modo que se obtiene:

kyon

La intensidad que interactua ($I_i$) es la fracci n definida por ERROR:8393 de la intensidad incidente ($I_s$), calculada de la siguiente manera:

kyon

La intensidad absorbida ($I_a$) es el complemento de la fracci n reflejada, calculada utilizando el albedo ($a$) y la intensidad incidente ($I_s$) de la siguiente manera:

kyon

La intensidad absorbida ($I_a$) es el complemento de la fracci n reflejada, calculada utilizando el albedo ($a$) y la intensidad incidente ($I_s$) de la siguiente manera:

kyon

La intensidad reflejada ($I_r$) corresponde a la fracci n definida por el albedo ($a$) de la intensidad incidente ($I_s$):

kyon

La intensidad reflejada ($I_r$) corresponde a la fracci n definida por el albedo ($a$) de la intensidad incidente ($I_s$):

kyon