Transporte de nubes
Storyboard 
Las nubes son desplazadas por las corrientes de aire generadas por las diferencias de presiones en las distintas zonas. Cada gota es acelerada por efecto de fuerzas tipo Stokes hasta alcanzar la velocidad del aire en movimiento que pueden ser varios metros por segundo y que dependen de la altura sobre la tierra.
ID:(800, 0)
Desplazamiento horizontal
Definición 
Cuando corre viento por un lugar en que existen nubes o neblina el movimiento del aire comienza a ejercer fuerza sobre las pequeñas gotas pudiendo arrastrarlas.
ID:(7786, 0)
Medición de tamaño de gota en neblina
Imagen 
Las gotas de agua contenidas en la neblina son de un tamaño entre fracciones y algunas decenas de micrones:
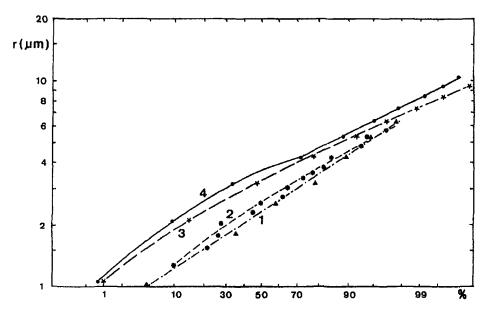
Distribución de gotas de neblina en distintas ubicaciones (Studia geoph. et geod. 41 (1997), 277-296)
Según la gráfica el 50% de las gotas tienen un radio inferior a unos 2.2 mu. Por ello podemos concluir que
> La típica gota de neblina tiene un radio de 2.2 mu
ID:(7815, 0)
Medición de tamaño de gota en lluvia
Nota 
Las gotas de lluvia son de un tamaño entre fracciones y algunos milímetros:
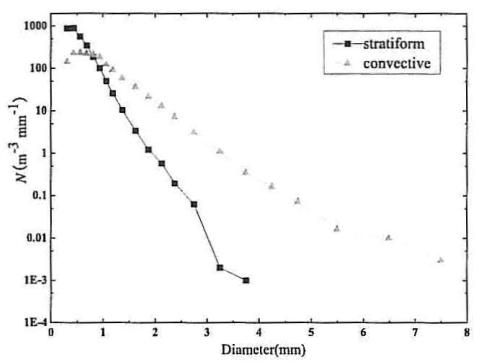
Distribución de gotas de lluvia según origen (Niu, J. Appl. Mcteor., 10 (2010), 632-645)
Según la gráfica, el máximo se encuentra en ambos casos para gotas que tienen un radio de alrededor de 0.5 mm. Por ello podemos concluir que
> La típica gota de lluvia tiene un radio de 0.5 mm
ID:(7816, 0)
Distancia Recorrida con $V=1\,m/s$
Cita 
Si se considera que el viento viaja a
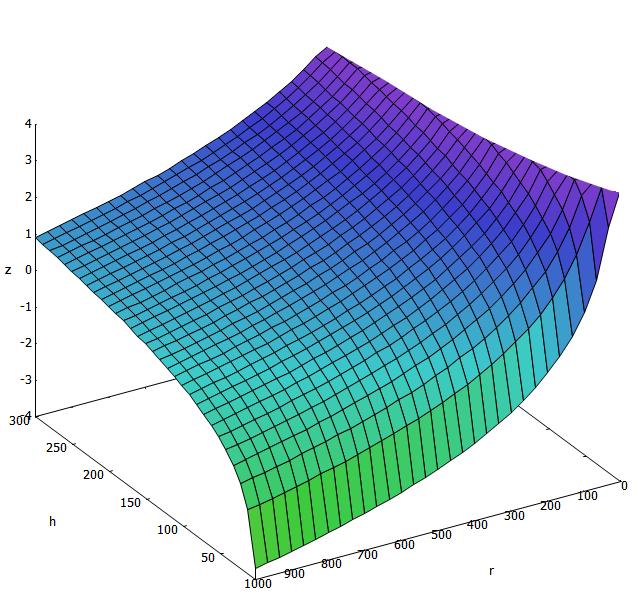
Distancia recorrida para viento de $1\,m/s$.\\n
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
ID:(7820, 0)
Distancia Recorrida con $V=5\,m/s$
Ejercicio 
Si se considera que el viento viaja a
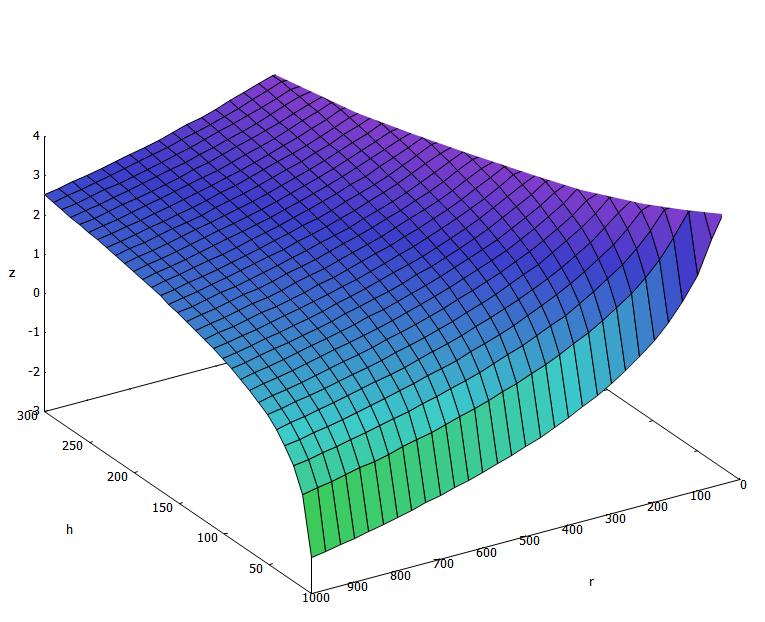
Distancia recorrida para viento de $5\,m/s$.\\n
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
ID:(7819, 0)
Distancia Recorrida con $V=10\,m/s$
Ecuación 
Si se considera que el viento viaja a
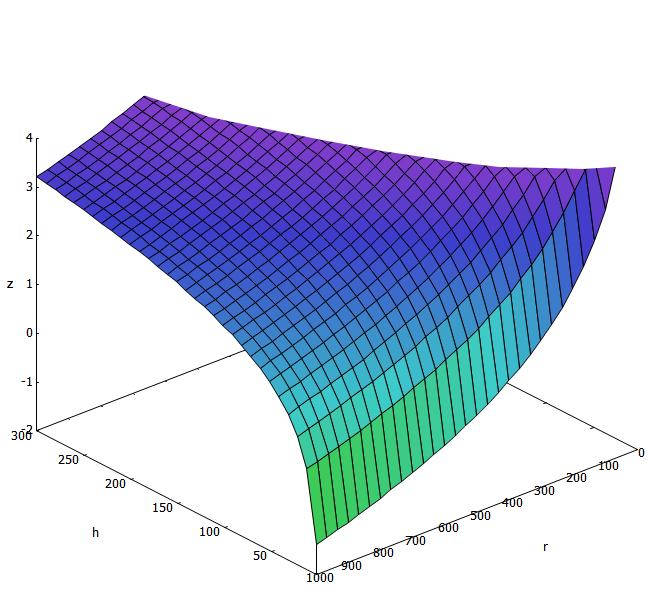
Distancia recorrida para viento de $10\,m/s$.
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
ID:(7821, 0)
Transporte de nubes
Storyboard 
Las nubes son desplazadas por las corrientes de aire generadas por las diferencias de presiones en las distintas zonas. Cada gota es acelerada por efecto de fuerzas tipo Stokes hasta alcanzar la velocidad del aire en movimiento que pueden ser varios metros por segundo y que dependen de la altura sobre la tierra.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Cuando corre viento por un lugar en que existen nubes o neblina el movimiento del aire comienza a ejercer fuerza sobre las peque as gotas pudiendo arrastrarlas.
La resistencia se define en funci n de la viscosidad del fluido y la velocidad de la esfera de la siguiente manera:
Stokes calcul expl citamente la resistencia experimentada por la esfera y determin que la viscosidad es proporcional al radio de la esfera y su velocidad, lo que lleva a la siguiente ecuaci n para la resistencia:
Como la fuerza que ejerce el viento de velocidad
se tiene que la velocidad de puede calcular de resolver la ecuaci n
donde
se tiene la ecuaci n
con el tiempo caracter stico
La soluci n es por ello
y concluimos que:
> *Las gotas de lluvia tienden a alcanzar en un tiempo igual al tiempo caracter stico $\tau$ la velocidad del viento.*
El tiempo caracter stico es
lo que permite estudiar en que escala de tiempo ocurre la aceleraci n.
Para gotas en una neblina o nube el radio medio lo podemos asumir como de
> *El arrastre de neblina por el viento es casi instant neo.*
En el caso de gotas de lluvia el radio es del orden de
> *El arrastre de gotas de lluvia por el viento muestra una inercia m nima.*
Las gotas de agua contenidas en la neblina son de un tama o entre fracciones y algunas decenas de micrones:
Seg n la gr fica el 50% de las gotas tienen un radio inferior a unos 2.2 mu. Por ello podemos concluir que
> La t pica gota de neblina tiene un radio de 2.2 mu
Las gotas de lluvia son de un tama o entre fracciones y algunos mil metros:
Seg n la gr fica, el m ximo se encuentra en ambos casos para gotas que tienen un radio de alrededor de 0.5 mm. Por ello podemos concluir que
> La t pica gota de lluvia tiene un radio de 0.5 mm
Si se integra la ecuaci n
en el tiempo se obtiene que el camino en el tiempo es igual a
Al ser la escala de tiempo que interesa mucho mayor que el tiempo caracter stico
> *Las gotas de neblina se mueven pr cticamente con la masa de aire en que est n suspendidas.*
> $x(t)=Vt$
Dado que el tiempo caracter stico es solo de algunos segundos se puede considerar que las gotas viajan a velocidad constante tanto con el viento como en su ca da. Por ello, si la velocidad del viento es
Como
se tiene que el tiempo de ca da ser
por lo que la distancia viajada ser
Por ello
> *La distancia recorrida es proporcional a la velocidad del viento y la altura inicial e inversamente proporcional al radio de la gota:*
> $d\propto\displaystyle\frac{Vh}{r^2}$
Si se considera que el viento viaja a
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
Si se considera que el viento viaja a
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
Si se considera que el viento viaja a
La parte superior recortada corresponde a distancias mayores que
Para el caso de lluvia (
Para el caso de neblina (
ID:(800, 0)
