Usuario:


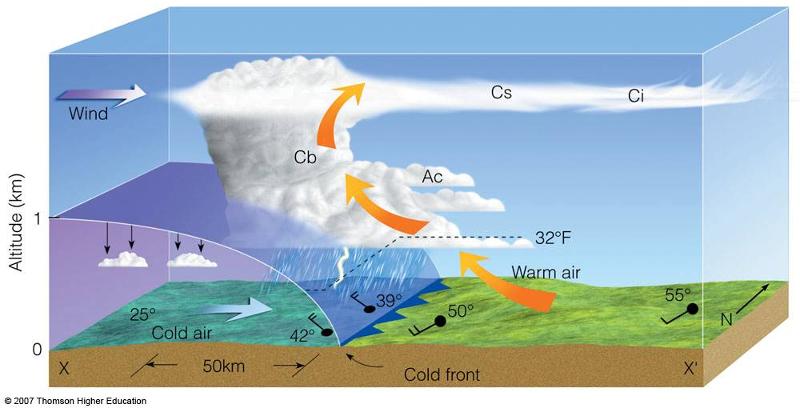
Formación de nubes
Storyboard

Las nubes se forman cuando el aire con humedad asciende, se dilata adiabaticamente por efecto de la menor presión llevando a su saturación y condensación que se vuelve visible como nubes.

>Modelo

ID:(553, 0)


Nubes y su covertura
Imagen

>Top


Según un informe del IPCC el promedio de cobertura por grosor óptico se distribuye en el planeta de la forma indicada en la siguiente imagen:

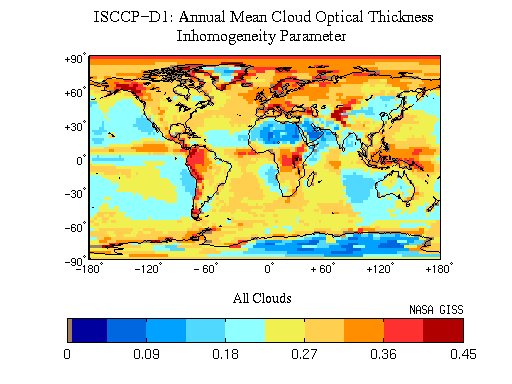
Grosor óptico medio anual * 100

En una estimación gruesa se puede estimar que el 10% de la superficie seria en el rango 0.0-3.6 o Cirrus, 70% en el rango 3.6-23 o Stratus y 20% en el rango 23-379 o Nimbus.

El grosor óptico de la nube se asocia al tipo de nube depende de la altura (r radio en um y r' radio efectivo um) y del tamaño de las gotas y su numero por centímetro cubico (N) de lo que depende el contenido de agua L en g/m3:

Medio | Tipo de nubes | r | r' | N | L

---------|---------------------|:----:|:-----:|:------:|:-----:

Continente | Stratus | 4.7 | 7.3 | 250 | 0.28

- | Cumulus (limpio) | 4.8 | 5.8 | 400 | 0.26

- | Cumulus (contaminado) | 3.5 | 4.0 | 1300 | 0.3

- | Cumulonimbus (creciendo)* | 6-8 | 7-10 | ~500 | 1-3

- | Cumulonimbus (disipando)* | 7-8 | 9-10 | ~300 | 1.0-1.5

- | Niebla | 8.1 | 10.7 | 15 | 0.06

Marino | Stratus | 6.7 | 11.3 | 80 | 0.30

- | Stratocumulus | 10.4 | 12.7 | 65 | 0.44

Continental o marino | Cirrus (-25C) | - | 92 | 0.11 | 0.03

- | Cirrus (-50C) | - | 57 | 0.02 | 0.002

ID:(3109, 0)


Temperatura
Php

>Top


La temperatura media en función de la latitud en general muestra un máximo en torno al ecuador y una reducción hacia los polos:

Adicionalmente se observa que se reduce con la altura.

ID:(9282, 0)


Concentración saturada en techo de la nube
Ecuación

>Top, >Modelo


Cuando la temperatura de la masa de aire en convección alcanza el punto de rocío se inicia el proceso de condensación. Si en ese momento la concentración de vapor de agua es c_i y cuando llega al techo de la nube es c_f entonces la fracción de vapor de agua que habrá condensado será igual a la diferencia:

$ \Delta c = c_i - c_f $

ID:(4874, 0)


Número de moles con masa molar
Ecuación

>Top, >Modelo


El número de moles ($n$) se determina dividiendo la masa ($M$) de una sustancia por su la masa molar ($M_m$), que corresponde al peso de un mol de la sustancia.

Por lo tanto, se puede establecer la siguiente relación:

$ n =\displaystyle\frac{ M }{ M_m }$

$M$
Masa
$kg$
$M_m$
Masa molar
$kg/mol$
$n$
Número de moles
$-$

La masa molar se expresa en gramos por mol (g/mol).

ID:(4854, 0)


Punto de rocío
Ecuación

>Top, >Modelo


De la relación de la presión del vapor de agua saturado

$ p_s = p_{ref} e^{- l_m / R T }$



se puede calcular con la humedad relativa RH (Relative Humidity) la presión de vapor de agua existente:

$ RH =\displaystyle\frac{ p_v }{ p_s }$



Como al bajar la temperatura la presión saturada va bajando existe una temperatura T_d (Dew point) en que la presión saturada alcanza la presión de vapor de agua existente p_v. Esto ocurre cuando

p_v(T_d)=p_0,e^{-l_m/RT_d}=RH,p_0,e^{-l_m/RT_s}=RH,p_s(T_s)

donde T_s es la temperatura inicial en que la humedad relativa era RH.

Si se despeja esta ecuación se obtiene la temperatura de rocío, es decir la temperatura límite en que el agua suspendida comenzaría a condensar:

$ T_d =\displaystyle\frac{ T }{1-\displaystyle\frac{ R T }{ l_m }\ln RH }$

ID:(4870, 0)


Temperatura de la masa que asciende en sección sin saturar
Ecuación

>Top, >Modelo


De la ecuación adiabática

$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$



y la ecuación para la presión que asciende:

$p(z)=p_0e^{-z/z_0}$



se tiene que si temperatura en la superficie es T_s la temperatura decrece como

$T(z)=T_se^{-(\kappa-1)z/\kappa z_0}$

ID:(42, 0)


Temperatura de la atmósfera en sección sin saturar
Ecuación

>Top, >Modelo


Si se asume un decrecimiento lineal entre la temperatura en la superficie T_e a T_b en la parte inferior de la atmósfera. Si esta ultima esta a una altura de z_b la temperatura tendría la forma

$T(z)=T_e-(T_e-T_b)\displaystyle\frac{z}{z_b}$

ID:(9939, 0)


Condición de formación de nubes
Descripción

>Top


La temperatura de la parte inferior de las nubes se definió en el modelo climático como T_b. La formación de dicha nube solo va a ser posible si la condensación ocurre antes de que la temperatura ambiente sea inferior a la temperatura de rocio:

$ T_d =\displaystyle\frac{ T }{1-\displaystyle\frac{ R T }{ l_m }\ln RH }$



lo que solo se da si la temperatura de la masa de aire que asciende es inferior a

$T_b <\displaystyle\frac{T}{1+\displaystyle\frac{RT}{l_m}ln(HR)}$

ID:(8841, 0)


Temperatura de la Masa que asciende en Sección Saturada
Ecuación

>Top, >Modelo


De la ecuación adiabática

$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$



y la ecuación para la presión que asciende:

$p(z)=p_0e^{-z/z_0}$



se tiene que un temperatura de rocio T_s a nivel de la parte inferior de la atmósfera donde inicia la condensación

$T(z)=T_de^{-(\kappa_s-1)(z-z_b)/\kappa_s z_0}$

en la altura z,

ID:(8839, 0)


Piso inferior de nubes
Ecuación

>Top, >Modelo


La nube se comienza a formar cuando el aire en asenso se enfría al punto que se inicia la condensación. Esto ocurre cuando se alcanza la temperatura de rocío T_d. Como la temperatura a una altura z esta dada por

$T(z)=T_se^{-(\kappa-1)z/\kappa z_0}$



se puede obtener que esto ocurre cuando la altura es igual a

$z_b=\displaystyle\frac{\kappa z_0}{(\kappa-1)}ln\displaystyle\frac{T_s}{T_d}$

ID:(8840, 0)


Límite de ascenso en función de la Temperatura
Ecuación

>Top, >Modelo


Como la temperatura es igual a

$T(z)=T_de^{-(\kappa_s-1)(z-z_b)/\kappa_s z_0}$



que alcanza la altura del techo de la nube cuando la temperatura es T_t o sea

T(z_t)=T_de^{-(\kappa_s-1)(z_t-z_b)/\kappa_s z_0}=T_t

que despejado permite calcular la altura máxima

$z_t=z_b+\displaystyle\frac{\kappa_s z_0}{(\kappa_s-1)}\ln\displaystyle\frac{T_d}{T_t}$

ID:(8837, 0)


Temperatura de la Atmósfera en Sección con Saturar
Ecuación

>Top, >Modelo


Si se asume un decrecimiento lineal entre la temperatura en la parte inferior de la atmósfera T_b a T_t en la parte superior de la atmósfera. Si esta ultima esta a una altura de z_t y la primera en z_b la temperatura tendría la forma

$T(z)=T_b-(T_b-T_t)\displaystyle\frac{(z-z_b)}{(z_t-z_b)}$

ID:(9940, 0)


Modelo simplificado para el calculo del CAPE
Imagen

>Top


En primera aproximación la dependencia de la temperatura con la altura tanto para el medio como para las adiabatas se pueden representar por rectas tanto para el sector no saturado como para aquel saturado:

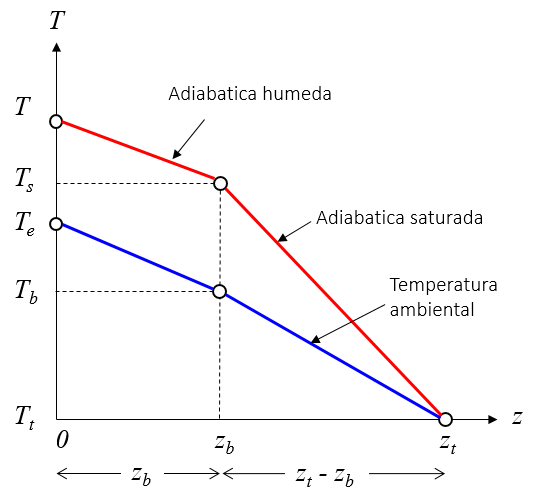
ID:(9941, 0)


Energía disponible para la convección
Ecuación

>Top, >Modelo


La clave para entender el ascenso es el calculo del CAPE

$CAPE=g\displaystyle\int_0^z ds\displaystyle\frac{(T(s)-T_m(s))}{T_m(s)}$



que corresponde a una medida de la energía potencial disponible para la convección.

Si se trabaja con un modelo simplificado en que la expresión la temperatura en el denominador se pueden aproximar por los valores medios

$\displaystyle\frac{1}{2}(T_e+T_b), \displaystyle\frac{1}{2}(T_d+T_t)$

respectivamente ya que al estar en grados Kelvin sus valores fluctúan en torno un numero medio mayor.

Por otro lado se pueden calcular las diferencias de las temperaturas mediante el calculo de los triángulos

$\displaystyle\frac{1}{2}(T_s-T_d)z_b,\displaystyle\frac{1}{2}(T_e-T_b)z_b, \displaystyle\frac{1}{2}(T_d-T_t)(z_b-z_t), \displaystyle\frac{1}{2}(T_b-T_t)(z_b-z_t)$

y rectángulos

$(T_d-T_b)z_b, (T_b-T_t)z_b$

que se observan en la gráfica del modelo simplificado.

Con ello se obtiene asi una estimación simple para el CAPE en la situación en que no existe un sector inhibidor:

$CAPE=g\left(\displaystyle\frac{(T_s+T_d)}{(T_e+T_b)}-1\right)z_b+g\displaystyle\frac{(T_d-T_b)}{(T_b+T_t)}(z_t-z_b)$

ID:(38, 0)